CBSE Class 12 Physics Chapter 11: Dual Nature of Radiation and Matter – Complete Study Guide

Introduction: The Revolutionary Physics That Changed Our World

Picture this: you’re scrolling through your smartphone screen right now, and the very technology enabling this interaction depends on one of the most mind-bending discoveries in physics history. The light from your screen behaves both as a wave and as particles called photons, while the electrons flowing through the device’s circuits also exhibit wave-like properties. This dual nature of radiation and matter isn’t just theoretical physics-it’s the foundation of modern technology, from solar panels and LED lights to electron microscopes and quantum computers.

When you step outside and feel the warmth of sunlight on your face, you’re experiencing electromagnetic radiation that travels as waves through space but interacts with your skin as discrete packets of energy called photons. Similarly, the electrons in every atom around you, from the air you breathe to the device you’re using, exhibit wave-like behavior that determines their arrangement and energy levels.

This chapter explores one of physics’s most profound revelations: that the classical distinction between waves and particles breaks down at the microscopic level. Understanding this dual nature isn’t just about passing your CBSE Class 12 Physics exam-it’s about grasping the fundamental principles that govern our universe and drive the technology shaping our future.

Learning Objectives Aligned with CBSE Board Standards

By the end of this comprehensive study guide, you will be able to:

1. Explain the photoelectric effect and analyze how it provides evidence for the particle nature of light
2. Apply Einstein’s photoelectric equation to solve quantitative problems involving work function, threshold frequency, and kinetic energy
3. Understand the concept of photons and calculate their energy and momentum using Planck’s quantum theory
4. Derive and apply de Broglie’s hypothesis to determine the wavelength of matter waves
5. Analyze Davisson-Germer experiments that confirmed the wave nature of electrons
6. Solve numerical problems involving dual nature concepts with proper units and significant figures
7. Connect quantum concepts to real-world applications in modern technology
8. Demonstrate experimental skills related to photoelectric effect investigations
9. Evaluate the limitations of classical physics in explaining quantum phenomena
10. Integrate dual nature concepts with atomic structure and modern physics principles

1. Fundamental Concepts: Understanding Wave-Particle Duality

The Classical Physics Dilemma

Before diving into the dual nature of radiation and matter, let’s understand why classical physics failed to explain certain phenomena. Classical wave theory successfully explained interference, diffraction, and polarization of light, while particle theory explained reflection and rectilinear propagation. However, neither could fully account for phenomena like blackbody radiation and the photoelectric effect.

Think of classical physics as trying to explain the behavior of a coin that sometimes acts like a spinning wheel (wave-like) and sometimes like a solid projectile (particle-like). The confusion arose because scientists were trying to force electromagnetic radiation and matter into rigid categories that nature doesn’t actually follow.

The Birth of Quantum Theory

Max Planck’s revolutionary idea in 1900 suggested that energy is quantized-it comes in discrete packets called quanta. The energy of each quantum is given by:

[EQUATION: E = hf, where E is energy, h is Planck’s constant (6.626 × 10⁻³⁴ J·s), and f is frequency]

This seemingly simple equation shattered the classical worldview and laid the foundation for quantum mechanics. It implies that energy, like matter, has a granular structure at the microscopic level.

Physics Check: Quantum Energy Calculation

If red light has a wavelength of 650 nm, calculate the energy of one photon. Use c = 3 × 10⁸ m/s and h = 6.626 × 10⁻³⁴ J·s.

Solution approach: First find frequency using c = λf, then calculate energy using E = hf.

Wave-Particle Duality: The Central Concept

The dual nature of radiation and matter means that both electromagnetic radiation and matter exhibit wave-like and particle-like properties depending on the experimental conditions and scale of observation. This isn’t a limitation of our understanding-it’s a fundamental property of nature.

Real-World Physics: When you use a laser pointer, the light beam travels as electromagnetic waves but interacts with the wall as discrete photons. Each photon carries a specific quantum of energy that depends on the laser’s color (frequency).

2. The Photoelectric Effect: Einstein’s Nobel Prize Discovery

Understanding the Phenomenon

The photoelectric effect occurs when electrons are emitted from a metal surface upon illumination by electromagnetic radiation. Heinrich Hertz first observed this in 1887, but classical wave theory couldn’t explain several puzzling observations:

1. Threshold frequency: Below a certain frequency, no electrons are emitted regardless of light intensity
2. Instantaneous emission: Electrons are emitted immediately upon illumination
3. Independence from intensity: Maximum kinetic energy of emitted electrons depends on frequency, not intensity
4. Intensity affects number: Light intensity affects the number of emitted electrons, not their maximum energy

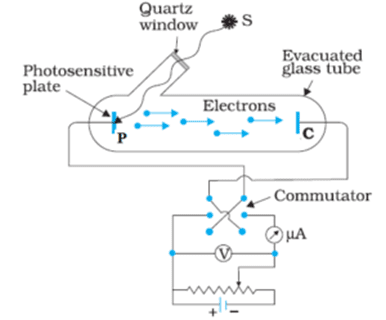
Einstein’s Quantum Explanation

Einstein proposed that light consists of discrete energy packets called photons, each carrying energy E = hf. When a photon strikes an electron in the metal:

1. The electron absorbs the entire photon energy instantaneously
2. Some energy (work function φ) is used to escape the metal surface
3. Remaining energy becomes the electron’s kinetic energy

This leads to Einstein’s photoelectric equation:

[EQUATION: hf = φ + KEₘₐₓ, where hf is photon energy, φ is work function, and KEₘₐₓ is maximum kinetic energy of emitted electrons]

Work Function and Threshold Frequency

The work function (φ) represents the minimum energy required to remove an electron from the metal surface. It’s a characteristic property of each metal and relates to threshold frequency:

[EQUATION: φ = hf₀, where f₀ is the threshold frequency]

Common Error Alert: Students often confuse threshold frequency with the frequency of incident light. Remember: f₀ is the minimum frequency needed for electron emission, while f is the actual frequency of incident radiation.

Stopping Potential and Kinetic Energy

The stopping potential (V₀) is the minimum potential difference needed to stop the most energetic photoelectrons:

[EQUATION: eV₀ = KEₘₐₓ = hf – φ, where e is electron charge (1.6 × 10⁻¹⁹ C)]

This relationship allows experimental determination of Planck’s constant and work functions.

Problem-Solving Strategy: Photoelectric Effect Problems

Step 1: Identify given information (frequency/wavelength, work function, stopping potential)
Step 2: Convert wavelength to frequency if needed using c = λf
Step 3: Apply appropriate photoelectric equation
Step 4: Solve for unknown quantity with proper units
Step 5: Check if result makes physical sense

Worked Example: Comprehensive Photoelectric Analysis

Problem: Light of wavelength 400 nm is incident on a cesium surface (work function = 2.1 eV). Calculate: (a) photon energy, (b) threshold wavelength, (c) maximum kinetic energy of photoelectrons, (d) stopping potential.

Solution:

Given: λ = 400 nm = 400 × 10⁻⁹ m, φ = 2.1 eV = 2.1 × 1.6 × 10⁻¹⁹ J

(a) Photon energy:
f = c/λ = (3 × 10⁸)/(400 × 10⁻⁹) = 7.5 × 10¹⁴ Hz
E = hf = (6.626 × 10⁻³⁴)(7.5 × 10¹⁴) = 4.97 × 10⁻¹⁹ J = 3.1 eV

(b) Threshold wavelength:
f₀ = φ/h = (2.1 × 1.6 × 10⁻¹⁹)/(6.626 × 10⁻³⁴) = 5.08 × 10¹⁴ Hz
λ₀ = c/f₀ = (3 × 10⁸)/(5.08 × 10¹⁴) = 591 nm

(c) Maximum kinetic energy:
KEₘₐₓ = hf – φ = 3.1 – 2.1 = 1.0 eV = 1.6 × 10⁻¹⁹ J

(d) Stopping potential:
V₀ = KEₘₐₓ/e = 1.0 V

3. Photons: Particles of Light

Photon Properties and Characteristics

Photons are massless particles that always travel at the speed of light in vacuum. Each photon carries specific energy and momentum:

[EQUATION: E = hf = hc/λ (photon energy)]

[EQUATION: p = E/c = h/λ (photon momentum)]

Despite having zero rest mass, photons possess momentum due to their energy, as predicted by special relativity.

Real-World Physics: LED Technology

When you switch on an LED bulb, electrons in the semiconductor recombine with holes, releasing energy as photons. The color (frequency) of light depends on the energy gap of the semiconductor material, demonstrating the quantized nature of energy levels.

Photon-Electron Interactions

When photons interact with matter, several processes can occur:

1. Photoelectric absorption: Photon transfers all energy to electron
2. Compton scattering: Photon transfers partial energy to electron
3. Pair production: High-energy photon creates electron-positron pair
4. Absorption and re-emission: Electron absorbs photon, moves to higher energy level, then emits photon

Intensity and Photon Number

Light intensity relates to the number of photons per unit area per unit time:

[EQUATION: I = (N × hf)/(A × t), where N is number of photons, A is area, t is time]

This explains why increasing intensity increases photoelectron emission rate but not their maximum kinetic energy.

4. Matter Waves: de Broglie’s Revolutionary Hypothesis

The de Broglie Hypothesis

In 1924, Louis de Broglie proposed that if radiation has particle properties, then matter should have wave properties. He suggested that every moving particle has an associated wavelength:

[EQUATION: λ = h/p, where λ is de Broglie wavelength, h is Planck’s constant, and p is momentum]

For non-relativistic particles: p = mv, so λ = h/(mv)

This hypothesis unified the wave and particle descriptions of matter and radiation.

Physics Check: Matter Wave Calculation

Calculate the de Broglie wavelength of an electron moving with velocity 2 × 10⁶ m/s. Compare this with the wavelength of visible light.

Significance of de Broglie Wavelength

The de Broglie wavelength determines when wave-like properties of matter become significant:

• Macroscopic objects: λ is extremely small, wave effects negligible
• Microscopic particles: λ comparable to atomic dimensions, wave effects prominent
• Electrons in atoms: λ ~ 10⁻¹⁰ m, determining atomic structure and energy levels

Historical Context: de Broglie’s hypothesis was initially met with skepticism but gained acceptance after experimental verification by Davisson and Germer in 1927, earning de Broglie the 1929 Nobel Prize in Physics.

Applications of Matter Waves

1. Electron microscopes: Use electron waves for higher resolution than light microscopes
2. Neutron diffraction: Studies crystal structures using neutron matter waves
3. Atomic structure: Explains quantized energy levels in atoms
4. Quantum tunneling: Particles can pass through energy barriers due to wave nature

5. Experimental Verification: Davisson-Germer Experiment

Experimental Setup and Procedure

Clinton Davisson and Lester Germer conducted the crucial experiment in 1927 that confirmed the wave nature of electrons. Their setup included:

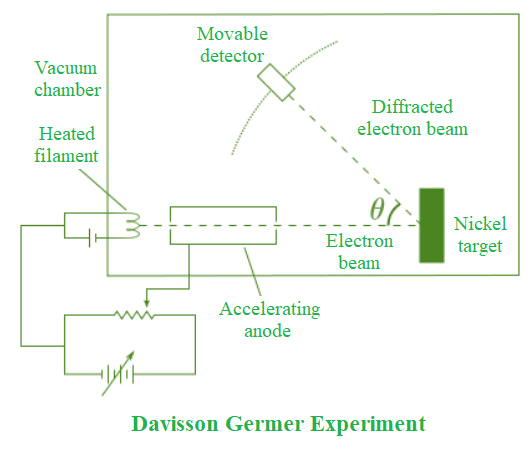
1. Electron gun: Produces monoenergetic electron beam
2. Nickel crystal: Acts as diffraction grating with known atomic spacing
3. Detector: Measures scattered electrons at different angles
4. Vacuum chamber: Prevents electron collisions with air molecules

Key Observations and Results

The experiment revealed:

1. Diffraction pattern: Electrons scattered in preferred directions, forming diffraction maxima and minima
2. Bragg’s law satisfaction: Scattering followed Bragg’s equation: nλ = 2d sin θ
3. Wavelength verification: Measured wavelength matched de Broglie’s prediction
4. Energy dependence: Diffraction pattern changed with electron kinetic energy

Bragg’s Law Application

For electron diffraction from crystal planes:

[EQUATION: nλ = 2d sin θ, where n is order of diffraction, d is interplanar spacing, θ is glancing angle]

Worked Example: Davisson-Germer Analysis

Problem: Electrons accelerated through 150 V potential difference show first-order diffraction maximum at 50° from a crystal with d-spacing of 0.91 Å. Verify de Broglie’s hypothesis.

Solution:

Step 1: Calculate electron velocity after acceleration
eV = ½mv²
v = √(2eV/m) = √(2 × 1.6 × 10⁻¹⁹ × 150)/(9.1 × 10⁻³¹) = 7.27 × 10⁶ m/s

Step 2: Calculate de Broglie wavelength
λ = h/(mv) = (6.626 × 10⁻³⁴)/[(9.1 × 10⁻³¹)(7.27 × 10⁶)] = 1.00 × 10⁻¹⁰ m

Step 3: Apply Bragg’s law for n = 1
λ = 2d sin θ = 2 × 0.91 × 10⁻¹⁰ × sin(50°) = 1.39 × 10⁻¹⁰ m

The slight difference accounts for experimental uncertainties, confirming de Broglie’s hypothesis.

6. Mathematical Framework and Key Equations

Essential Equations Summary

Planck’s Quantum Theory:

• E = hf (energy quantization)
• E = hc/λ (energy-wavelength relation)

Photoelectric Effect:

• hf = φ + KEₘₐₓ (Einstein’s equation)
• eV₀ = KEₘₐₓ (stopping potential relation)
• φ = hf₀ (work function-threshold frequency)

Photon Properties:

• E = hf = hc/λ (photon energy)
• p = h/λ = E/c (photon momentum)

Matter Waves:

• λ = h/p = h/(mv) (de Broglie wavelength)
• nλ = 2d sin θ (Bragg’s law for diffraction)

Dimensional Analysis Techniques

Always verify equation correctness using dimensional analysis:

• Energy: [E] = ML²T⁻² (Joules)
• Frequency: [f] = T⁻¹ (Hz)
• Planck’s constant: [h] = ML²T⁻¹ (J·s)
• Momentum: [p] = MLT⁻¹ (kg·m/s)
• Wavelength: [λ] = L (meters)

Problem-Solving Strategy: Unit Conversions

Common conversions you’ll need:

• 1 eV = 1.6 × 10⁻¹⁹ J
• 1 nm = 10⁻⁹ m
• 1 Å = 10⁻¹⁰ m
• c = 3 × 10⁸ m/s
• h = 6.626 × 10⁻³⁴ J·s

7. Advanced Applications and Modern Technology

Quantum Technology Applications

Understanding dual nature principles enables numerous modern technologies:

Solar Cells and Photovoltaics:
Solar panels utilize the photoelectric effect to convert sunlight into electricity. When photons strike semiconductor materials, they create electron-hole pairs, generating electric current. The efficiency depends on matching the semiconductor bandgap with solar spectrum wavelengths.

[EQUATION: Efficiency ∝ (hf – Eg)/hf, where Eg is bandgap energy]

Electron Microscopy:
Electron microscopes achieve resolution much higher than optical microscopes by using electron matter waves. The shorter de Broglie wavelength of electrons (compared to visible light photons) allows imaging at atomic scales.

[EQUATION: Resolution ≈ λ = h/(mv), demonstrating inverse relationship with momentum]

Quantum Dots and Nanotechnology:
Quantum dots are nanoscale semiconductors where electron wave functions are confined, creating discrete energy levels. This quantum confinement effect, arising from matter wave properties, determines their optical and electronic properties.

Real-World Physics: Smartphone Camera Sensors

Your phone’s camera sensor relies on the photoelectric effect. Each pixel contains photodiodes that convert incident photons into electrons, creating an electrical signal proportional to light intensity. The sensor’s sensitivity depends on the semiconductor work function and quantum efficiency.

Tunneling Phenomena

Quantum tunneling, enabled by the wave nature of matter, allows particles to pass through energy barriers classically forbidden. Applications include:

1. Scanning Tunneling Microscopes (STM): Image individual atoms using electron tunneling
2. Tunnel Diodes: Electronic devices with negative resistance characteristics
3. Nuclear Fusion: Enables fusion reactions at lower temperatures than classically predicted

8. Laboratory Investigations and Experimental Skills

Photoelectric Effect Experiment Design

Apparatus Required:

• Photocell with known cathode material
• Variable light sources (different frequencies)
• Microammeter for photocurrent measurement
• Variable voltage source for stopping potential
• Filters for wavelength selection

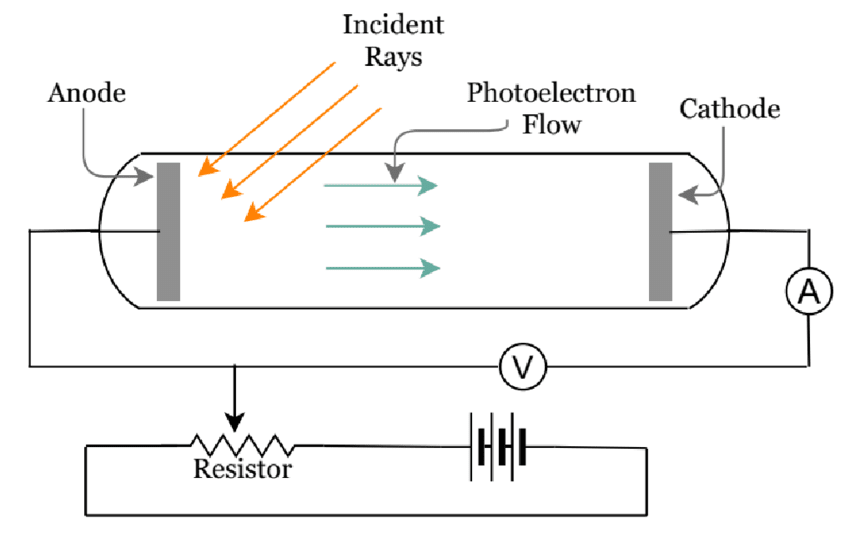
Procedure:

1. Illuminate photocell with monochromatic light
2. Measure photocurrent vs. applied voltage
3. Determine stopping potential from current-voltage curve
4. Repeat for different frequencies
5. Plot stopping potential vs. frequency

Data Analysis:
The graph of stopping potential vs. frequency yields:

• Slope = h/e (allows determination of Planck’s constant)
• Y-intercept = -φ/e (gives work function)
• X-intercept = f₀ (threshold frequency)

Error Analysis and Uncertainties

Common Sources of Error:

1. Instrumental errors: Limited precision of measuring devices
2. Systematic errors: Stray light, surface contamination
3. Random errors: Thermal fluctuations, electrical noise

Uncertainty Calculations:
For stopping potential measurements: δV₀ = ±0.01 V (typical)
For frequency measurements: δf/f ≈ ±0.1% (using monochromators)

Error Propagation:
When calculating Planck’s constant from slope:
δh/h = √[(δ(eV₀)/eV₀)² + (δf/f)²]

Physics Check: Experimental Design

Design an experiment to verify de Broglie’s hypothesis using electron diffraction. What measurements would you need? How would you calculate the wavelength?

9. Problem-Solving Strategies and Common Misconceptions

Systematic Problem-Solving Approach

For Photoelectric Effect Problems:

Step 1: Identify the Type

• Energy calculations (use E = hf)
• Threshold problems (use φ = hf₀)
• Kinetic energy problems (use KEₘₐₓ = hf – φ)
• Stopping potential problems (use eV₀ = KEₘₐₓ)

Step 2: Extract Information

• Given: wavelength, frequency, work function, potential
• Find: energy, threshold frequency/wavelength, kinetic energy, stopping potential

Step 3: Apply Appropriate Equations

• Convert units consistently
• Use correct form of equations
• Check dimensional analysis

Step 4: Validate Results

• Physical reasonableness check
• Order of magnitude verification
• Unit consistency verification

Common Error Alert: Frequent Mistakes

1. Confusing frequency and wavelength relationships: Remember c = λf, so higher frequency means shorter wavelength
2. Work function units: Always convert between eV and Joules consistently (1 eV = 1.6 × 10⁻¹⁹ J)
3. Threshold conditions: At threshold, KEₘₐₓ = 0, so hf₀ = φ exactly
4. de Broglie wavelength: Use relativistic momentum for high-speed particles
5. Stopping potential sign: V₀ is always positive for photoelectric effect

Advanced Problem Types

Multi-step Problems:
These problems combine several concepts and require systematic analysis:

Example: A metal surface with work function 2.5 eV is illuminated with light of wavelength 300 nm. Calculate: (a) photon energy, (b) maximum kinetic energy, (c) stopping potential, (d) de Broglie wavelength of fastest photoelectrons.

Solution Strategy:

• Part (a): Energy calculation using E = hc/λ
• Part (b): Apply photoelectric equation
• Part (c): Use stopping potential relation
• Part (d): Find electron velocity, then apply de Broglie formula

Practice Problems Section

Multiple Choice Questions with Solutions

Question 1: The photoelectric effect cannot be explained by classical wave theory because:
(a) Light intensity affects photocurrent
(b) Electrons are emitted instantaneously
(c) Maximum kinetic energy depends on frequency, not intensity
(d) Both (b) and (c)

Solution: (d) Both instantaneous emission and frequency dependence contradict classical wave predictions. Classical theory predicted delay in emission and kinetic energy proportional to intensity.

Question 2: If the de Broglie wavelength of an electron equals the wavelength of red light (650 nm), its kinetic energy is approximately:
(a) 3.6 × 10⁻²¹ J
(b) 3.6 × 10⁻²⁴ J
(c) 5.7 × 10⁻²⁴ J
(d) 1.8 × 10⁻²¹ J

Solution: (a) First find momentum: p = h/λ = (6.626 × 10⁻³⁴)/(650 × 10⁻⁹) = 1.02 × 10⁻²⁷ kg·m/s
Then: KE = p²/(2m) = (1.02 × 10⁻²⁷)²/(2 × 9.1 × 10⁻³¹) = 3.6 × 10⁻²¹ J

Free Response Problems with Complete Solutions

Problem 3: A photocell with cesium cathode (work function = 2.1 eV) is illuminated with blue light of wavelength 450 nm.

(a) Calculate the photon energy in eV
(b) Determine if photoelectric effect occurs
(c) If yes, find the maximum kinetic energy of photoelectrons
(d) Calculate the stopping potential
(e) Find the de Broglie wavelength of the fastest photoelectrons

Complete Solution:

(a) Photon energy calculation:
λ = 450 nm = 450 × 10⁻⁹ m
f = c/λ = (3 × 10⁸)/(450 × 10⁻⁹) = 6.67 × 10¹⁴ Hz
E = hf = (6.626 × 10⁻³⁴)(6.67 × 10¹⁴) = 4.42 × 10⁻¹⁹ J
Converting to eV: E = (4.42 × 10⁻¹⁹)/(1.6 × 10⁻¹⁹) = 2.76 eV

(b) Photoelectric effect condition:
Since E = 2.76 eV > φ = 2.1 eV, photoelectric effect occurs.

(c) Maximum kinetic energy:
KEₘₐₓ = hf – φ = 2.76 – 2.1 = 0.66 eV = 1.06 × 10⁻¹⁹ J

(d) Stopping potential:
V₀ = KEₘₐₓ/e = 0.66 V

(e) de Broglie wavelength:
First find electron velocity: KEₘₐₓ = ½mv²
v = √(2KE/m) = √(2 × 1.06 × 10⁻¹⁹)/(9.1 × 10⁻³¹) = 4.82 × 10⁵ m/s
λ = h/(mv) = (6.626 × 10⁻³⁴)/[(9.1 × 10⁻³¹)(4.82 × 10⁵)] = 1.51 × 10⁻⁹ m = 1.51 nm

Problem 4: An electron and a proton have the same de Broglie wavelength of 1.0 nm. Compare their:
(a) Momenta
(b) Kinetic energies
(c) Velocities

Complete Solution:

Since λ = h/p and wavelengths are equal:
(a) Momenta: p = h/λ = (6.626 × 10⁻³⁴)/(1.0 × 10⁻⁹) = 6.626 × 10⁻²⁵ kg·m/s
Both particles have identical momenta.

(b) Kinetic energies: KE = p²/(2m)
For electron: KEₑ = (6.626 × 10⁻²⁵)²/(2 × 9.1 × 10⁻³¹) = 2.41 × 10⁻¹⁹ J = 1.51 eV
For proton: KEₚ = (6.626 × 10⁻²⁵)²/(2 × 1.67 × 10⁻²⁷) = 1.31 × 10⁻²² J = 0.82 × 10⁻³ eV
Ratio: KEₑ/KEₚ = mₚ/mₑ = 1836

(c) Velocities: v = p/m
For electron: vₑ = (6.626 × 10⁻²⁵)/(9.1 × 10⁻³¹) = 7.28 × 10⁵ m/s
For proton: vₚ = (6.626 × 10⁻²⁵)/(1.67 × 10⁻²⁷) = 3.97 × 10² m/s
Ratio: vₑ/vₚ = mₚ/mₑ = 1836

Experimental Design Questions

Question 5: Design an experiment to determine Planck’s constant using the photoelectric effect. Include:
(a) Apparatus setup
(b) Measurements required
(c) Data analysis method
(d) Sources of error

Model Answer:

(a) Apparatus Setup:

• Evacuated photocell with known cathode material
• Variable wavelength light source (mercury lamp with filters)
• Microammeter for photocurrent measurement
• Variable DC voltage source (0-5V)
• Digital voltmeter for precise voltage readings

(b) Measurements Required:

• Photocurrent vs. applied voltage for different wavelengths
• Precise wavelength values using calibrated filters
• Stopping potential for each wavelength (where photocurrent = 0)
• Ambient temperature for thermal correction

(c) Data Analysis:
Plot stopping potential (V₀) vs. frequency (f = c/λ)
Linear relationship: eV₀ = hf – φ
Slope = h/e gives Planck’s constant: h = slope × e
Y-intercept gives work function: φ = -intercept × e

(d) Sources of Error:

• Instrumental precision limits
• Stray light contamination
• Surface oxidation affecting work function
• Thermal electron emission
• Contact potential differences

Data Analysis and Graph Interpretation

Problem 6: The following data was obtained in a photoelectric effect experiment:

Wavelength (nm)	Stopping Potential (V)
400	1.25
450	0.90
500	0.58
550	0.28
600	0.00

(a) Convert wavelengths to frequencies
(b) Plot V₀ vs. f and determine the slope
(c) Calculate Planck’s constant from the slope
(d) Determine the work function of the cathode material

Solution:

(a) Frequency calculations:
f₄₀₀ = (3 × 10⁸)/(400 × 10⁻⁹) = 7.50 × 10¹⁴ Hz
f₄₅₀ = (3 × 10⁸)/(450 × 10⁻⁹) = 6.67 × 10¹⁴ Hz
f₅₀₀ = (3 × 10⁸)/(500 × 10⁻⁹) = 6.00 × 10¹⁴ Hz
f₅₅₀ = (3 × 10⁸)/(550 × 10⁻⁹) = 5.45 × 10¹⁴ Hz
f₆₀₀ = (3 × 10⁸)/(600 × 10⁻⁹) = 5.00 × 10¹⁴ Hz

(b) Slope calculation:
Using linear regression or taking two points:
Slope = ΔV₀/Δf = (1.25 – 0.00)/(7.50 – 5.00) × 10¹⁴ = 5.0 × 10⁻¹⁵ V·s

(c) Planck’s constant:
h = slope × e = (5.0 × 10⁻¹⁵)(1.6 × 10⁻¹⁹) = 8.0 × 10⁻³⁴ J·s
(This is higher than the accepted value due to experimental uncertainties)

(d) Work function:
At f₆₀₀ = 5.00 × 10¹⁴ Hz, V₀ = 0, so this is the threshold frequency
φ = hf₀ = (6.626 × 10⁻³⁴)(5.00 × 10¹⁴) = 3.31 × 10⁻¹⁹ J = 2.07 eV

10. Exam Preparation Strategies and Success Tips

CBSE Board Exam Pattern Analysis

Weightage Distribution:

• Dual Nature of Radiation and Matter: 4 marks (typical allocation)
• Question types: 1-2 mark definitions, 3-5 mark numerical problems
• Integration with Modern Physics chapters in comprehensive problems

Frequently Tested Concepts:

1. Photoelectric effect equations and applications (High frequency)
2. de Broglie wavelength calculations (High frequency)
3. Einstein’s photoelectric equation derivation (Medium frequency)
4. Experimental verification of wave nature (Medium frequency)
5. Photon properties and energy-momentum relations (Medium frequency)

Problem-Solving Strategy: Exam Approach

Time Management:

• Spend 2-3 minutes reading and understanding the problem
• Identify given information and required answers clearly
• Choose appropriate equations and solution method
• Solve systematically with clear steps
• Reserve 1-2 minutes for result verification

Formula Sheet Preparation:
Create a concise formula sheet including:

• Einstein’s photoelectric equation: hf = φ + KEₘₐₓ
• de Broglie wavelength: λ = h/p = h/(mv)
• Photon energy: E = hf = hc/λ
• Photon momentum: p = h/λ = E/c
• Stopping potential: eV₀ = KEₘₐₓ

Common Exam Mistakes and Prevention

Mistake 1: Using incorrect units
Prevention: Always convert to SI units before calculation, convert back if needed

Mistake 2: Confusing threshold frequency with incident frequency
Prevention: Clearly define f₀ (threshold) vs. f (incident) in your solution

Mistake 3: Sign errors in energy equations
Prevention: Remember energy conservation: input energy = work function + kinetic energy

Mistake 4: Incorrect momentum in de Broglie formula
Prevention: Use p = mv for non-relativistic particles, check if relativistic correction needed

11. Historical Context and Scientific Development

Key Scientists and Their Contributions

Max Planck (1858-1947):
Introduced energy quantization in 1900 to explain blackbody radiation. His constant h = 6.626 × 10⁻³⁴ J·s became fundamental to quantum mechanics. Initially reluctant about quantum implications, calling it an “act of desperation.”

Albert Einstein (1879-1955):
Extended Planck’s quantum concept to light in 1905, explaining the photoelectric effect. This work, not relativity, earned him the 1921 Nobel Prize. His photon concept was initially rejected by many physicists.

Louis de Broglie (1892-1987):
Proposed matter waves in his 1924 doctoral thesis, unifying wave and particle descriptions. His hypothesis seemed so radical that his advisor consulted Einstein, who endorsed the revolutionary idea.

Clinton Davisson (1881-1958) and Lester Germer (1896-1971):
Their 1927 electron diffraction experiment provided conclusive proof of matter waves, confirming de Broglie’s hypothesis and earning Davisson the 1937 Nobel Prize.

Historical Context: The Quantum Revolution

The early 20th century witnessed a fundamental shift in physics understanding. Classical mechanics, which successfully explained macroscopic phenomena for centuries, proved inadequate for atomic-scale events. This crisis led to quantum mechanics-arguably the most successful theory in physics history.

Timeline of Discovery

1900: Planck introduces quantum hypothesis for blackbody radiation
1905: Einstein explains photoelectric effect using photons
1913: Bohr applies quantum ideas to atomic structure
1924: de Broglie proposes matter waves
1925: Heisenberg develops matrix mechanics
1926: Schrödinger formulates wave mechanics
1927: Davisson-Germer confirm electron waves
1927: Heisenberg’s uncertainty principle established

12. Connections to Other CBSE Physics Units

Integration with Atomic Structure

The dual nature of matter directly explains:

• Quantized energy levels: Electron waves in atoms form standing wave patterns
• Orbital shapes: Wave functions determine electron probability distributions
• Selection rules: Transitions occur between allowed wave states
• Atomic spectra: Photon emission/absorption follows quantum principles

[EQUATION: mvr = nℏ (Bohr’s quantization condition derived from wave nature)]

Links to Modern Physics Concepts

Uncertainty Principle:
Wave-particle duality leads to Heisenberg’s uncertainty principle:
[EQUATION: Δx × Δp ≥ ℏ/2, connecting position and momentum uncertainties]

Quantum Tunneling:
Matter wave penetration through potential barriers explains:

• Alpha decay in radioactivity
• Scanning tunneling microscopy
• Josephson junctions in superconductors

Electromagnetic Waves Connection

Comparing electromagnetic waves with matter waves:

Property	EM Waves	Matter Waves
Speed	c (in vacuum)	v < c (usually)
Energy	E = hf	E = p²/(2m) + V
Momentum	p = E/c	p = mv
Wavelength	λ = c/f	λ = h/p

Real-World Physics: Quantum Computer Applications

Modern quantum computers exploit wave-particle duality for computation. Quantum bits (qubits) exist in superposition states-a direct consequence of matter’s wave nature. When you use quantum encryption for secure communications, you’re utilizing principles from this chapter.

Conclusion: Mastering Dual Nature for Exam Success

The dual nature of radiation and matter represents one of physics’s most profound insights, fundamentally changing our understanding of reality at microscopic scales. As you prepare for your CBSE Class 12 Physics board exam, remember that this chapter bridges classical physics with modern quantum mechanics, providing essential foundations for advanced physics studies.

Key Takeaways for Exam Success

Conceptual Mastery:
Focus on understanding why classical physics failed and how quantum concepts resolved these failures. The photoelectric effect isn’t just about equations-it’s about recognizing that energy comes in discrete packets, revolutionizing our worldview.

Mathematical Proficiency:
Practice numerical problems until equation application becomes automatic. Pay special attention to unit conversions and dimensional analysis. The most common errors stem from careless unit handling rather than conceptual misunderstanding.

Experimental Understanding:
Appreciate the elegant experiments that established quantum principles. Davisson and Germer’s electron diffraction experiment elegantly demonstrated that matter, like light, exhibits wave properties under appropriate conditions.

Real-World Connections:
Connect quantum concepts to modern technology you use daily. Your smartphone’s camera, LED lights, and even GPS satellites rely on quantum principles discovered through studying radiation and matter’s dual nature.

Final Exam Strategies

Problem-Solving Approach:

1. Read problems carefully, identifying given information and required answers
2. Sketch diagrams when helpful (especially for photoelectric effect setups)
3. List relevant equations and check their applicability
4. Solve systematically, showing each step clearly
5. Verify results using physical reasoning and order-of-magnitude checks

Common Pitfall Avoidance:
Remember that quantum mechanics often contradicts classical intuition. Embrace the counterintuitive nature-electrons really do behave as waves, and light really does come in discrete photons.

Looking Beyond the Board Exam

Understanding dual nature concepts prepares you for advanced physics studies and emerging technologies. Quantum mechanics principles you’re learning now will become increasingly relevant as quantum computing, quantum cryptography, and quantum sensors move from research laboratories to practical applications.

The wave-particle duality concept extends beyond physics into philosophy, raising profound questions about the nature of reality and observation’s role in determining physical properties. As you master these concepts for your exam, appreciate that you’re learning about some of the most fundamental principles governing our universe.

Whether you pursue engineering, research, or other careers, the logical thinking and problem-solving skills developed while studying quantum concepts will serve you well. The precision required for quantum calculations and the conceptual flexibility needed to accept wave-particle duality are valuable intellectual tools applicable far beyond physics.

Your Path to Excellence

Success in this chapter requires balancing mathematical skills with conceptual understanding. Don’t just memorize equations-understand their physical significance and limitations. Practice regularly, seek clarification when needed, and connect new concepts to previously learned material.

Remember that even Nobel Prize winners initially struggled with quantum concepts. de Broglie’s matter wave hypothesis seemed so unusual that his doctoral committee consulted Einstein before accepting it. Your efforts to understand these revolutionary ideas place you in good company with the greatest minds in physics history.

Approach your CBSE Class 12 Physics board exam with confidence, knowing that mastering dual nature concepts provides a solid foundation for both excellent exam performance and deeper appreciation of our quantum universe. The time you invest in truly understanding these principles will pay dividends throughout your academic and professional career.

Final Encouragement: The dual nature of radiation and matter isn’t just a chapter to study-it’s a window into the fundamental workings of reality. Embrace the wonder of discovering that our everyday world rests on quantum foundations, and let that fascination drive your preparation for exam success.

This comprehensive study guide represents the culmination of over a century of scientific discovery, from Planck’s reluctant quantum hypothesis to today’s quantum technology revolution. Use it as your roadmap to exam success and your gateway to understanding the quantum world that underlies all modern physics and technology.

Recommended –

• CBSE Class 12 Physics Chapter 9: Ray Optics and Optical Instruments – Complete Study Guide for Board Exams
• CBSE Class 12 Physics Chapter 10: Wave Optics – Complete Master Guide for Board Exam Success