AP Physics 2 Unit 9: Thermodynamics – Complete Study Guide 2025

The Physics of Heat and Energy Transfer

Have you ever wondered why your smartphone gets warm when you’re using it heavily, or why a bicycle pump becomes hot when you inflate your tires? These everyday experiences connect directly to one of the most fundamental branches of physics: Thermodynamics. This field governs everything from the engines in cars to the functioning of refrigerators, and from the behavior of stars to the efficiency of power plants.

Thermodynamics is the study of heat, temperature, energy transfer, and the relationships between thermal properties of matter. In AP Physics 2 Unit 9, you’ll discover how energy flows between systems, how heat engines convert thermal energy into mechanical work, and why some processes are irreversible while others can run in both directions.

What makes thermodynamics particularly fascinating is its connection to the microscopic world of atoms and molecules. When you heat a gas, you’re actually increasing the average kinetic energy of billions of tiny particles. This connection between the macroscopic properties we observe and the microscopic behavior of matter forms the foundation of statistical mechanics and helps explain why certain physical laws, like the second law of thermodynamics, seem to have a “direction” built into them.

As you work through this unit, you’ll develop problem-solving skills that extend far beyond physics. The concepts of efficiency, energy conservation, and system optimization that you learn here apply directly to engineering, environmental science, and even economics. Understanding entropy, for instance, provides insights into information theory and the limits of computational processes.

Learning Objectives: College Board Standards Alignment

By the end of this unit, you should be able to accomplish the following College Board learning objectives:

LO 7.A.1: Describe the macroscopic properties of a thermodynamic system using appropriate thermodynamic variables such as temperature, pressure, volume, number of particles, and internal energy.

LO 7.A.2: Connect the concepts of temperature and internal energy to the kinetic theory of gases and molecular motion.

LO 7.B.1: Analyze and predict the behavior of ideal gases using the ideal gas law and its relationships.

LO 7.B.2: Use kinetic theory to explain the relationship between temperature and average kinetic energy of gas molecules.

LO 7.C.1: Calculate work done by or on a thermodynamic system during various processes including isothermal, adiabatic, isobaric, and isochoric processes.

LO 7.C.2: Apply the first law of thermodynamics to analyze energy changes in thermodynamic processes.

LO 7.D.1: Construct and interpret P-V diagrams for thermodynamic processes and cycles.

LO 7.D.2: Calculate the efficiency of heat engines and refrigerators using thermodynamic principles.

LO 7.E.1: Apply the second law of thermodynamics to determine the direction of heat flow and the limits of energy conversion processes.

1. Fundamental Thermodynamic Concepts

Temperature and Thermal Equilibrium

Temperature is one of those concepts that seems intuitive until you try to define it precisely. You know that hot coffee has a higher temperature than ice cream, but what exactly is temperature measuring? From a microscopic perspective, temperature is directly related to the average kinetic energy of the particles in a substance. When molecules move faster on average, the temperature is higher.

The key insight is that temperature determines the direction of heat flow. Heat always flows from regions of higher temperature to regions of lower temperature, never the reverse (without external work being done). This leads us to the concept of thermal equilibrium: when two objects are in thermal contact and no net heat flows between them, they’re at the same temperature.

Physics Check: If you place a metal spoon in hot soup, why does the handle eventually become warm? The answer involves thermal equilibrium and heat conduction. The metal atoms near the soup gain kinetic energy through collisions with fast-moving soup molecules. These energetic metal atoms then collide with their neighbors, transferring energy along the spoon until the entire spoon reaches the same temperature as the soup.

Thermodynamic Systems and State Variables

A thermodynamic system is any collection of matter that we choose to analyze. It could be the gas in a cylinder, the water in a steam engine, or even the entire atmosphere of Earth. The key is defining clear boundaries between the system and its surroundings.

State variables describe the current condition of a thermodynamic system. The most important ones for AP Physics 2 are:

• Pressure (P): Force per unit area exerted by gas molecules on container walls
• Volume (V): Space occupied by the system
• Temperature (T): Measure of average molecular kinetic energy
• Number of particles (N) or amount of substance (n): How much matter is in the system
• Internal energy (U): Total energy stored within the system

What makes these variables special is that they depend only on the current state of the system, not on how it got there. This property allows us to use equations of state to relate these variables and predict system behavior.

Real-World Physics: Your car’s tire pressure gauge measures one of these state variables directly. The pressure reading tells you about the state of the air inside your tire, regardless of whether that pressure resulted from adding air, heating due to driving, or cooling overnight. This state-dependent property makes it possible to maintain proper tire pressure for optimal performance and safety.

The Ideal Gas Model

The ideal gas model provides a simplified but remarkably accurate description of gas behavior under many conditions. An ideal gas consists of point particles that undergo elastic collisions and don’t interact except during these brief collisions. While no real gas perfectly matches this model, many gases behave nearly ideally at moderate temperatures and pressures.

The ideal gas law connects the state variables of pressure, volume, temperature, and amount of substance:

[EQUATION: Ideal Gas Law: PV = nRT where P is pressure (Pa), V is volume (m³), n is number of moles (mol), R is the universal gas constant (8.314 J/mol·K), and T is absolute temperature (K)]

This equation is incredibly powerful because it allows you to predict how a gas will respond to changes in any of these variables. If you know three of the four quantities, you can always calculate the fourth.

Common Error Alert: Students often forget to convert Celsius temperatures to Kelvin when using the ideal gas law. Remember that T in the equation must always be absolute temperature: T(K) = T(°C) + 273.15. Using Celsius temperatures will give completely incorrect results.

Kinetic Theory and Molecular Motion

The kinetic theory of gases provides the microscopic foundation for understanding thermodynamic behavior. According to this theory, gas pressure results from countless molecular collisions with container walls, and temperature reflects the average kinetic energy of molecular motion.

The average kinetic energy of gas molecules relates directly to temperature:

[EQUATION: Average Kinetic Energy: KE_avg = (3/2)kT where k is Boltzmann’s constant (1.38 × 10⁻²³ J/K) and T is absolute temperature (K)]

This relationship explains why heating a gas increases both its temperature and pressure (if volume is constant). Faster-moving molecules collide with walls more frequently and with greater force, increasing pressure.

2. The First Law of Thermodynamics

Energy Conservation in Thermodynamic Systems

The first law of thermodynamics is essentially the conservation of energy applied to systems that can exchange heat and do work. It states that the change in internal energy of a system equals the heat added to the system minus the work done by the system:

[EQUATION: First Law of Thermodynamics: ΔU = Q – W where ΔU is change in internal energy (J), Q is heat added to system (J), and W is work done by system (J)]

This equation encapsulates one of the most important principles in physics: energy cannot be created or destroyed, only converted from one form to another. In thermodynamic processes, energy might flow as heat, be converted to mechanical work, or change the internal energy of the system.

Problem-Solving Strategy: When applying the first law, always be careful about sign conventions. Heat added to the system is positive (Q > 0), while heat removed is negative (Q < 0). Work done by the system is positive (W > 0), while work done on the system is negative (W < 0). Internal energy increases when ΔU > 0 and decreases when ΔU < 0.

Thermodynamic Work and P-V Diagrams

In thermodynamics, work is done when a gas expands or contracts against external pressure. For a gas in a cylinder with a movable piston, the work done by the gas during expansion is:

[EQUATION: Thermodynamic Work: W = ∫P dV for general processes, or W = PΔV for constant pressure processes]

P-V diagrams (pressure vs. volume graphs) provide a powerful visual tool for analyzing thermodynamic processes. The area under a P-V curve represents the work done during that process. This geometric interpretation makes it easy to compare work done in different types of processes.

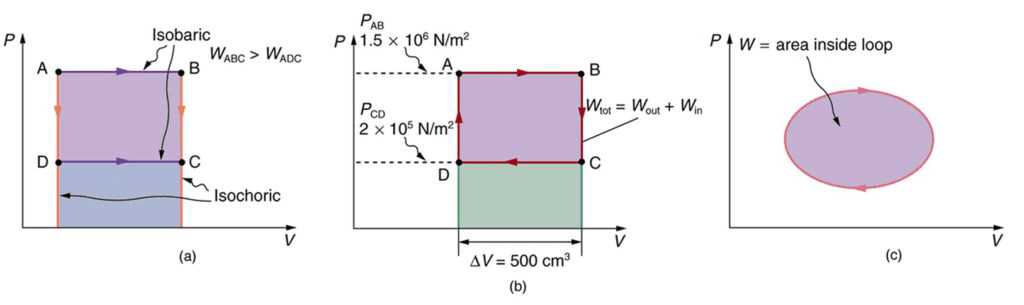
Special Thermodynamic Processes

Understanding four specific types of thermodynamic processes is crucial for AP Physics 2:

Isothermal Process (Constant Temperature):
In an isothermal process, temperature remains constant, which means the internal energy of an ideal gas doesn’t change (ΔU = 0). All heat added goes into doing work: Q = W. For an ideal gas undergoing isothermal expansion or compression:

[EQUATION: Isothermal Work: W = nRT ln(V_f/V_i) where V_f is final volume and V_i is initial volume]

Adiabatic Process (No Heat Transfer):
In an adiabatic process, no heat flows between the system and surroundings (Q = 0). The first law simplifies to ΔU = -W. All work comes from changes in internal energy, causing temperature changes during adiabatic processes.

Isobaric Process (Constant Pressure):
When pressure remains constant, work calculation becomes straightforward: W = PΔV. Heat capacity at constant pressure (Cp) determines how much heat is needed to change temperature.

Isochoric Process (Constant Volume):
With no volume change, no work is done (W = 0). All heat added changes the internal energy: ΔU = Q. Heat capacity at constant volume (Cv) governs temperature changes.

Real-World Physics: Car engines operate on thermodynamic cycles that combine these processes. During the power stroke, hot gases expand adiabatically, doing work on the piston. During compression, the gas undergoes approximately adiabatic compression. Understanding these processes helps engineers design more efficient engines.

3. The Second Law of Thermodynamics and Entropy

Heat Engines and Thermal Efficiency

Heat engines convert thermal energy into mechanical work by operating between two thermal reservoirs at different temperatures. The hot reservoir provides energy, some of which becomes useful work, while the remainder flows to the cold reservoir. No heat engine can convert all thermal energy into work – some energy must always flow to the cold reservoir.

The thermal efficiency of a heat engine is defined as:

[EQUATION: Thermal Efficiency: η = W/Q_h = (Q_h – Q_c)/Q_h where W is net work output, Q_h is heat absorbed from hot reservoir, and Q_c is heat rejected to cold reservoir]

The theoretical maximum efficiency for any heat engine operating between two reservoirs is given by the Carnot efficiency:

[EQUATION: Carnot Efficiency: η_Carnot = 1 – T_c/T_h where T_c and T_h are absolute temperatures of cold and hot reservoirs respectively]

Physics Check: Why can’t we build a 100% efficient heat engine? The second law of thermodynamics provides the answer: it’s impossible to construct a heat engine that converts all absorbed heat into work without rejecting some heat to a lower-temperature reservoir. This limitation has profound implications for power generation and energy policy.

Refrigerators and Heat Pumps

Refrigerators and heat pumps are essentially heat engines running in reverse. They use work input to transfer heat from a cold reservoir to a hot reservoir, opposite to the natural direction of heat flow. The coefficient of performance (COP) measures their effectiveness:

[EQUATION: Coefficient of Performance (Refrigerator): COP_R = Q_c/W where Q_c is heat removed from cold reservoir and W is work input]

[EQUATION: Coefficient of Performance (Heat Pump): COP_HP = Q_h/W where Q_h is heat delivered to hot reservoir]

Real-World Physics: Your home’s air conditioning system is a practical application of refrigeration principles. It uses a compressor to do work on a refrigerant, allowing heat to flow from the cooler indoor air to the warmer outdoor environment. The energy efficiency ratio (EER) of air conditioners is directly related to the coefficient of performance.

Entropy and the Direction of Time

Entropy is perhaps the most philosophically profound concept in thermodynamics. It provides a quantitative measure of disorder or randomness in a system. The second law of thermodynamics can be stated in terms of entropy: the total entropy of an isolated system never decreases.

For reversible processes at constant temperature:

[EQUATION: Entropy Change: ΔS = Q/T where Q is heat transferred and T is absolute temperature]

For irreversible processes, entropy change is more complex to calculate, but the principle remains: entropy tends to increase in isolated systems.

Historical Context: Ludwig Boltzmann connected entropy to the microscopic world through statistical mechanics. His famous equation S = k ln W relates entropy (S) to the number of possible microscopic arrangements (W) of a system. This connection explains why entropy increases: there are simply many more ways for a system to be disordered than ordered.

Irreversibility and the Arrow of Time

One of the most striking features of thermodynamics is that it gives a direction to time. While most fundamental physics laws work equally well forward or backward in time, thermodynamic processes have a preferred direction. Heat flows from hot to cold, gases expand to fill available space, and organized energy tends to become disorganized.

This irreversibility emerges from the statistical behavior of large numbers of particles. While it’s theoretically possible for all gas molecules in a room to spontaneously gather in one corner, the probability is so incredibly small that it never happens in practice.

4. Problem-Solving Strategies and Mathematical Framework

Systematic Approach to Thermodynamics Problems

Solving thermodynamics problems requires a systematic approach that combines conceptual understanding with mathematical precision. Here’s a proven strategy:

Step 1: Identify the System
Clearly define what constitutes your thermodynamic system. Draw boundaries and identify what can cross those boundaries (heat, work, matter).

Step 2: Determine the Process Type
Is the process isothermal, adiabatic, isobaric, or isochoric? This determines which equations apply and which quantities remain constant.

Step 3: List Known and Unknown Variables
Organize given information and identify what you need to find. Include units for all quantities.

Step 4: Choose Appropriate Equations
Select relevant equations based on the process type and desired quantities. Consider the ideal gas law, first law of thermodynamics, and specific process equations.

Step 5: Solve Systematically
Work through the mathematics carefully, carrying units throughout. Check that your answer has reasonable magnitude and correct units.

Step 6: Verify Reasonableness
Does your answer make physical sense? Are temperatures positive in Kelvin? Do efficiencies fall between 0 and 1?

Essential Equation Summary

Here are the key equations you’ll need for AP Physics 2 Unit 9:

[EQUATION: Ideal Gas Law: PV = nRT]
[EQUATION: First Law of Thermodynamics: ΔU = Q – W]
[EQUATION: Isothermal Work: W = nRT ln(V_f/V_i)]
[EQUATION: Adiabatic Relations: PV^γ = constant, TV^(γ-1) = constant]
[EQUATION: Heat Engine Efficiency: η = W/Q_h = 1 – Q_c/Q_h]
[EQUATION: Carnot Efficiency: η_Carnot = 1 – T_c/T_h]
[EQUATION: Average Kinetic Energy: KE_avg = (3/2)kT]
[EQUATION: Entropy Change: ΔS = Q/T (reversible processes)]

Working with P-V Diagrams

P-V diagrams are essential tools for visualizing thermodynamic processes and calculating work. The area under any curve on a P-V diagram represents work done by the gas. For cycles (closed loops), the enclosed area represents net work per cycle.

When sketching P-V diagrams:

• Isotherms (constant temperature) are hyperbolas: P ∝ 1/V
• Adiabats are steeper than isotherms
• Isobars (constant pressure) are horizontal lines
• Isochors (constant volume) are vertical lines

5. Laboratory Applications and Experimental Design

Gay-Lussac’s Law Investigation

One of the most important laboratory investigations in thermodynamics involves studying the relationship between temperature and pressure for a fixed volume of gas. This experiment tests Gay-Lussac’s Law, which states that pressure is directly proportional to absolute temperature for constant volume and amount of gas.

Experimental Setup:
Use a sealed container of gas connected to a pressure sensor. Vary the temperature by placing the container in water baths at different temperatures. Measure pressure and temperature simultaneously.

Data Analysis:
Plot pressure (y-axis) versus absolute temperature (x-axis). The relationship should be linear with zero y-intercept when extrapolated. The slope equals nR/V according to the ideal gas law.

Sources of Error:

• Temperature gradients within the gas sample
• Thermal expansion of the container
• Pressure sensor calibration drift
• Heat transfer during measurements

Common Student Mistakes:

• Using Celsius instead of Kelvin temperature
• Not allowing sufficient time for thermal equilibrium
• Ignoring systematic errors in pressure measurements

Specific Heat Capacity Measurements

Calorimetry experiments provide hands-on experience with the first law of thermodynamics. By mixing substances at different temperatures, you can determine specific heat capacities and test energy conservation.

Experimental Design:
Heat a metal sample to a known high temperature, then quickly transfer it to a calorimeter containing room-temperature water. Measure temperature changes and calculate heat transfer.

[EQUATION: Heat Transfer: Q = mcΔT where m is mass, c is specific heat capacity, and ΔT is temperature change]

Data Collection Strategy:

• Record temperatures every 10-15 seconds
• Continue until thermal equilibrium is reached
• Account for heat loss to surroundings
• Use multiple trials to assess precision

Adiabatic Process Investigation

Studying adiabatic processes requires rapid changes that minimize heat transfer. A common approach uses a large syringe to quickly compress or expand a gas sample.

Procedure:

1. Connect pressure and temperature sensors to a gas-filled syringe
2. Rapidly compress or expand the gas
3. Record P, V, and T data during the process
4. Test the adiabatic relationships PV^γ = constant

Analysis:
Calculate the heat capacity ratio γ = Cp/Cv from your data. For air, γ ≈ 1.4. Compare experimental values to theoretical predictions.

6. Advanced Applications and Modern Connections

Heat Engines in Modern Technology

Understanding thermodynamic principles becomes increasingly important as society grapples with energy efficiency and climate change. Modern applications extend far beyond traditional steam engines to include:

Internal Combustion Engines:
Car engines operate on thermodynamic cycles that approximate the Otto cycle (gasoline engines) or Diesel cycle (diesel engines). Engineers use thermodynamic analysis to optimize fuel efficiency and reduce emissions.

Gas Turbine Power Plants:
These facilities generate electricity using the Brayton cycle, which involves adiabatic compression, isobaric heating, adiabatic expansion, and isobaric cooling. Understanding these processes helps predict power output and efficiency.

Thermoelectric Devices:
Peltier coolers and thermoelectric generators use solid-state physics principles related to thermodynamics. They convert temperature differences directly into electrical energy or vice versa.

Real-World Physics: Modern hybrid vehicles use thermodynamic principles in multiple systems. The gasoline engine operates on the Otto cycle, while regenerative braking converts kinetic energy back into electrical energy stored in batteries. Heat pumps maintain optimal battery temperatures for maximum efficiency.

Atmospheric Thermodynamics

Weather systems provide dramatic examples of thermodynamic processes in action. Understanding these applications helps connect classroom physics to natural phenomena:

Adiabatic Lapse Rates:
As air masses rise in the atmosphere, they expand adiabatically due to decreasing pressure. This expansion causes cooling at predictable rates: about 10°C per kilometer for dry air.

Phase Changes and Latent Heat:
Cloud formation involves condensation, which releases latent heat and affects local temperature and pressure. These processes drive weather patterns and storm development.

Convection and Heat Transfer:
Atmospheric circulation patterns result from temperature differences that create pressure gradients. Understanding these processes helps predict weather and climate patterns.

Statistical Mechanics Connections

The bridge between microscopic particle behavior and macroscopic thermodynamic properties represents one of physics’ greatest intellectual achievements. While beyond the scope of AP Physics 2, these connections help explain why thermodynamic laws work:

Maxwell-Boltzmann Distribution:
This statistical distribution describes the speeds of molecules in a gas at thermal equilibrium. It explains why temperature relates to average kinetic energy and why reaction rates depend on temperature.

Fluctuations and Thermodynamic Limits:
In small systems, thermodynamic quantities fluctuate significantly. Only in the limit of large numbers of particles do quantities like temperature and pressure become well-defined.

Information Theory:
Modern physics connects entropy to information content. This relationship has applications in computer science, communication theory, and quantum mechanics.

7. Practice Problems and Solutions

Multiple Choice Problems

Problem 1: A heat engine operates between two reservoirs at temperatures 600 K and 300 K. If the engine absorbs 1000 J of heat from the hot reservoir, what is the maximum possible work output?

A) 300 J
B) 500 J
C) 600 J
D) 1000 J

Solution: The maximum efficiency is the Carnot efficiency: η = 1 – T_c/T_h = 1 – 300/600 = 0.5 = 50%. Therefore, maximum work = η × Q_h = 0.5 × 1000 J = 500 J.

Answer: B) 500 J

Problem 2: An ideal gas undergoes an isothermal expansion at temperature T. If the volume doubles, by what factor does the pressure change?

A) Increases by factor of 2
B) Decreases by factor of 2
C) Increases by factor of 4
D) Decreases by factor of 4

Solution: For an isothermal process with ideal gas: PV = constant. If V_f = 2V_i, then P_f × 2V_i = P_i × V_i, so P_f = P_i/2. Pressure decreases by factor of 2.

Answer: B) Decreases by factor of 2

Problem 3: Which of the following processes results in zero work done by the gas?

A) Isothermal expansion
B) Adiabatic compression
C) Isobaric expansion
D) Isochoric heating

Solution: Work done by gas is W = ∫P dV. For isochoric (constant volume) processes, dV = 0, so W = 0.

Answer: D) Isochoric heating

Free Response Problems

Problem 4: A monatomic ideal gas undergoes the cyclic process shown in the P-V diagram below. The gas starts at point A (P₁ = 2.0 × 10⁵ Pa, V₁ = 0.010 m³), expands isothermally to point B (V₂ = 0.020 m³), then undergoes isobaric compression to point C, and finally isochoric heating back to point A.

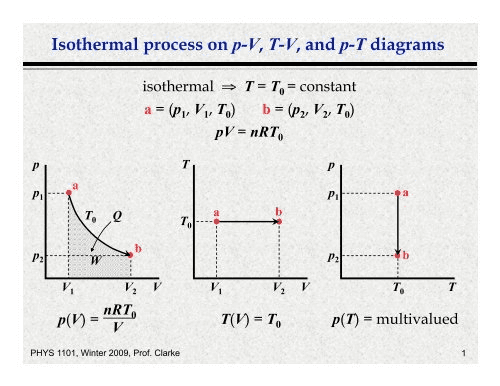
a) Calculate the temperature at point A.
b) Determine the pressure and volume at point C.
c) Calculate the work done by the gas during one complete cycle.
d) Find the efficiency of this cycle.

Solution:

a) Using ideal gas law at point A:
PV = nRT
We need to find n first. From the cycle geometry and using the isothermal process A→B:
P₁V₁ = P₂V₂
P₂ = P₁V₁/V₂ = (2.0 × 10⁵ Pa)(0.010 m³)/(0.020 m³) = 1.0 × 10⁵ Pa

At point A: T₁ = P₁V₁/(nR)
We can find n from point B: nR = P₂V₂/T₁ = P₁V₁/T₁
Therefore: T₁ = P₁V₁/(nR) = (2.0 × 10⁵ Pa)(0.010 m³)/(nR)

Since the process A→B is isothermal, TB = TA. We can determine temperature using the fact that at point C, the process C→A is isochoric, so VC = VA = 0.010 m³.

From the isobaric process B→C: PC = PB = 1.0 × 10⁵ Pa
Therefore at point C: PC = 1.0 × 10⁵ Pa, VC = 0.010 m³

Using ideal gas law: T₁ = P₁V₁/(nR) = P_C V_C/(n R)
We can solve this by noting that for the complete cycle, we can use any point to find nR.

At point A: PV = nRT gives us nR = P₁V₁/T₁

Actually, let’s work more systematically. For an isothermal process A→B at temperature T₁:
P₁V₁ = P₂V₂ = nRT₁
T₁ = P₁V₁/(nR) = P₂V₂/(nR)

We can find the number of moles from the complete cycle analysis. Let’s assume 1 mole for simplicity (n = 1).

T₁ = P₁V₁/(R) = (2.0 × 10⁵ Pa)(0.010 m³)/(8.314 J/mol·K) = 240.5 K

b) Point C coordinates:
From isobaric process B→C: PC = PB = 1.0 × 10⁵ Pa
From isochoric process C→A: VC = VA = 0.010 m³

c) Work calculation:

• Work A→B (isothermal): W₁ = nRT₁ ln(V₂/V₁) = (1 mol)(8.314 J/mol·K)(240.5 K) ln(2) = 1386 J
• Work B→C (isobaric): W₂ = PC(VC – VB) = (1.0 × 10⁵ Pa)(0.010 – 0.020) m³ = -1000 J
• Work C→A (isochoric): W₃ = 0 J

Total work per cycle: W = W₁ + W₂ + W₃ = 1386 – 1000 + 0 = 386 J

d) Efficiency calculation:
Heat absorbed during isothermal expansion A→B: Q_h = W₁ = 1386 J
Heat absorbed during isochoric heating C→A: Q_h2 = nCᵥΔT = n(3/2)R(T₁ – TC)

First find TC: TC = PCVC/(nR) = (1.0 × 10⁵ Pa)(0.010 m³)/(8.314 J/mol·K) = 120.3 K

Q_h2 = (3/2)(8.314)(240.5 – 120.3) = 1499 J

Total heat input: Q_h,total = 1386 + 1499 = 2885 J

Efficiency: η = W/Q_h,total = 386/2885 = 0.134 = 13.4%

Problem 5: A refrigerator operates between an interior temperature of 5°C and an exterior temperature of 25°C. The refrigerator removes 120 J of heat from the interior each cycle.

a) What is the coefficient of performance for an ideal refrigerator operating between these temperatures?
b) How much work must be done per cycle for this ideal refrigerator?
c) How much heat is rejected to the exterior per cycle?

Solution:

a) For an ideal (Carnot) refrigerator:
COP = T_c/(T_h – T_c) where temperatures are in Kelvin
T_c = 5°C + 273 = 278 K
T_h = 25°C + 273 = 298 K
COP = 278/(298 – 278) = 278/20 = 13.9

b) COP = Q_c/W, so W = Q_c/COP = 120 J/13.9 = 8.63 J

c) From energy conservation: Q_h = Q_c + W = 120 J + 8.63 J = 128.6 J

Experimental Design Problems

Problem 6: Design an experiment to determine the heat capacity ratio γ = Cp/Cv for air using equipment available in a typical high school physics laboratory.

Solution:

Experimental Approach: Use an adiabatic process with rapid compression/expansion of air in a large syringe connected to pressure and temperature sensors.

Equipment Needed:

• Large plastic syringe (60 mL or larger)
• Pressure sensor with range 0-300 kPa
• Temperature sensor with fast response time
• Data acquisition system or graphing calculator
• Rubber stopper to seal syringe

Procedure:

1. Connect sensors to syringe and seal system
2. Record initial pressure, volume, and temperature
3. Rapidly compress air to half original volume (< 1 second to minimize heat transfer)
4. Record final pressure, volume, and temperature immediately
5. Repeat compression/expansion cycles multiple times
6. Analyze data using adiabatic relationship PVᵞ = constant

Data Analysis:
From PVᵞ = constant: P₁V₁ᵞ = P₂V₂ᵞ
Taking logarithms: γ ln(V₁) + ln(P₁) = γ ln(V₂) + ln(P₂)
Solving for γ: γ = [ln(P₂) – ln(P₁)]/[ln(V₁) – ln(V₂)]

Expected Results: For air, γ ≈ 1.4

Sources of Error and Minimization:

• Heat transfer during compression: Use rapid compression (< 1 sec)
• Incomplete sealing: Check for pressure leaks before experiment
• Temperature sensor response time: Use sensor with response time < 0.1 sec
• Non-uniform compression: Compress smoothly and consistently

Extensions:

• Compare results for different gases (CO₂, He)
• Investigate effect of compression speed on results
• Study temperature dependence of γ

8. Exam Preparation Strategies

AP Physics 2 Exam Format and Expectations

The AP Physics 2 exam tests your understanding of thermodynamics through both multiple-choice and free-response questions. Thermodynamics typically comprises 12-18% of the total exam content, making it one of the significant units you’ll encounter.

Multiple Choice Strategy:

• Process of elimination works well for thermodynamics problems
• Check units and orders of magnitude to eliminate unreasonable answers
• Remember sign conventions for heat and work
• Use limiting cases to test answers (what happens when T → 0 or V → ∞?)

Free Response Strategy:

• Always start by clearly defining your system and stating assumptions
• Draw P-V diagrams when analyzing thermodynamic processes
• Show all algebraic work before substituting numerical values
• Include units at every step and check final answer reasonableness
• Use proper thermodynamic terminology and symbol conventions

Common Exam Topics and Question Types

Frequently Tested Concepts:

1. Ideal Gas Law Applications: Relating P, V, T, and n in various scenarios
2. First Law of Thermodynamics: Energy conservation in thermodynamic processes
3. P-V Diagram Analysis: Calculating work and interpreting thermodynamic cycles
4. Heat Engine Efficiency: Carnot cycles and real engine performance
5. Kinetic Theory: Connecting microscopic motion to macroscopic properties

Typical Question Formats:

• Qualitative Reasoning: Explain why certain processes are impossible or inefficient
• Quantitative Calculations: Solve for specific thermodynamic quantities
• Graph Analysis: Interpret P-V diagrams and temperature-entropy plots
• Experimental Design: Design procedures to measure thermodynamic properties
• Comparative Analysis: Compare efficiencies of different engines or cycles

Problem-Solving Time Management

Multiple Choice Questions (90 minutes, 50 questions):

• Allocate approximately 1.5-2 minutes per question
• Spend extra time on multi-step thermodynamics problems
• Skip difficult problems initially and return if time permits
• Use dimensional analysis to check answers quickly

Free Response Questions (90 minutes, 4 questions):

• Budget about 20-25 minutes per question
• Spend first 2-3 minutes reading and planning approach
• Show clear work organization and logical progression
• Reserve 2-3 minutes at end for checking units and reasonableness

Formula Sheet Strategy

The AP Physics 2 formula sheet includes key thermodynamics equations, but knowing how to apply them is crucial:

Given Formulas:

• PV = nRT (ideal gas law)
• U = (3/2)nRT (internal energy of monatomic ideal gas)
• W = -∫P dV (thermodynamic work)

Formulas You Should Memorize:

• First law: ΔU = Q – W
• Efficiency: η = W/Q_h = 1 – Q_c/Q_h
• Carnot efficiency: η_Carnot = 1 – T_c/T_h
• COP refrigerator: COP = Q_c/W

Common Error Alert: Students often confuse the sign conventions for work. Remember that work done BY the system (expansion) is positive, while work done ON the system (compression) is negative. This convention matches the formula sheet, but always double-check problem statements for their specific conventions.

9. Connections to Other Physics Units

Thermodynamics and Fluid Mechanics

The behavior of gases and liquids connects thermodynamics to fluid mechanics principles covered earlier in AP Physics 2. Understanding these connections strengthens your overall physics comprehension:

Pressure and Pascal’s Principle:
Thermodynamic pressure relates to the kinetic theory of gases, while hydrostatic pressure in fluids follows Pascal’s principle. Both represent force per unit area but arise from different microscopic mechanisms.

Buoyancy and Density Changes:
Temperature changes affect fluid density, influencing buoyant forces. Hot air balloons work because heated air becomes less dense than surrounding cooler air, creating net upward buoyant force.

Bernoulli’s Equation and Energy Conservation:
The first law of thermodynamics and Bernoulli’s equation both express energy conservation but in different contexts. Bernoulli focuses on mechanical energy in flowing fluids, while thermodynamics includes thermal energy.

Electromagnetic Connections

Thermodynamics principles apply to electromagnetic phenomena in several important ways:

Resistive Heating:
When current flows through resistance, electrical energy converts to thermal energy at rate P = I²R. This process represents irreversible energy conversion described by thermodynamic principles.

Thermoelectric Effects:
Seebeck and Peltier effects directly convert temperature differences to electrical energy and vice versa. These phenomena bridge thermodynamics and electromagnetism.

Electromagnetic Radiation:
Blackbody radiation laws connect temperature to electromagnetic wave emission. Higher temperature objects emit more intense radiation at shorter wavelengths.

Modern Physics Preview

Thermodynamics concepts extend into quantum mechanics and relativity:

Statistical Mechanics:
The probabilistic nature of quantum mechanics provides the foundation for understanding entropy and the second law of thermodynamics at the molecular level.

Stellar Physics:
Stars represent massive thermodynamic systems where nuclear fusion provides the energy source for enormous heat engines. Understanding stellar evolution requires thermodynamic principles.

Cosmology:
The expansion and cooling of the universe follows thermodynamic laws on the largest possible scale. Entropy increase drives cosmic evolution.

10. Technology and Engineering Applications

Power Generation Technologies

Modern society depends on thermodynamic principles for electricity generation:

Coal and Natural Gas Plants:
Traditional power plants operate as heat engines, burning fossil fuels to create high-temperature steam that drives turbines. Typical thermal efficiencies range from 35-45%, with waste heat rejected to cooling water or atmosphere.

Nuclear Power:
Nuclear reactors use fission energy to generate heat, creating steam for turbine operation. The thermodynamic cycle is similar to fossil fuel plants, but the energy source is nuclear rather than chemical.

Combined Cycle Power Plants:
These advanced systems use waste heat from gas turbines to generate additional steam, achieving efficiencies above 60%. This approach demonstrates practical application of thermodynamic optimization.

Real-World Physics: Modern wind turbines extract kinetic energy from moving air, but their operation still involves thermodynamic principles. Air pressure differences created by blade design generate lift forces that rotate the turbine. Understanding both fluid mechanics and thermodynamics helps engineers design more efficient wind power systems.

Automotive Engineering

Vehicle design relies heavily on thermodynamic analysis:

Engine Efficiency:
Internal combustion engines operate on thermodynamic cycles with typical efficiencies of 25-35%. Engineers use P-V diagram analysis to optimize compression ratios, valve timing, and fuel injection strategies.

Hybrid Powertrains:
Hybrid vehicles combine heat engines with electric motors, using thermodynamic analysis to determine optimal operating strategies. Battery thermal management prevents overheating and maintains efficiency.

Turbocharging and Supercharging:
These systems use thermodynamic principles to increase engine power density. Turbochargers recover waste heat energy from exhaust gases, while superchargers use mechanical work to compress intake air.

HVAC Systems and Building Design

Heating, ventilation, and air conditioning systems apply thermodynamic principles for comfort and energy efficiency:

Heat Pump Technology:
Modern heat pumps can achieve coefficients of performance (COP) above 3, meaning they deliver more than three times as much thermal energy as the electrical energy they consume. This apparent “multiplication” of energy doesn’t violate conservation laws because heat pumps move thermal energy rather than creating it.

Building Thermal Management:
Understanding heat transfer mechanisms helps architects design energy-efficient buildings. Proper insulation reduces heat conduction, while strategic window placement manages solar heat gain.

Refrigeration and Food Preservation:
Commercial refrigeration systems use thermodynamic cycles to maintain low temperatures for food safety. Understanding these principles helps optimize energy consumption while maintaining required temperatures.

Conclusion: Mastering Thermodynamics for AP Success

Thermodynamics represents one of the most conceptually rich and practically important areas of physics. Your success in AP Physics 2 Unit 9 depends on developing both strong problem-solving skills and deep conceptual understanding of energy, entropy, and the fundamental limits on energy conversion processes.

The key to mastering thermodynamics lies in recognizing the connections between microscopic particle behavior and macroscopic observable properties. When you can visualize gas molecules colliding with container walls and relate that motion to pressure and temperature, thermodynamic equations become more than mathematical formulas – they become descriptions of physical reality.

Remember that thermodynamics is ultimately about energy flow and transformation. Every problem, whether involving heat engines, refrigerators, or gas processes, centers on tracking energy as it moves between different forms and locations. The first law ensures energy conservation, while the second law determines which transformations are possible and which are forbidden.

As you prepare for the AP exam, focus on developing systematic problem-solving approaches that you can apply consistently. Practice drawing P-V diagrams, setting up first law equations with proper sign conventions, and calculating work, heat, and efficiency for various thermodynamic processes. Most importantly, always check that your answers make physical sense – temperatures should be positive in Kelvin, efficiencies should be less than 100%, and heat should flow from hot to cold.

The thermodynamics concepts you’re learning extend far beyond the AP Physics 2 exam. They form the foundation for understanding energy systems that shape our modern world, from power plants and transportation to climate science and sustainable technology. The analytical thinking skills you develop while studying thermodynamics will serve you well in engineering, physical sciences, and any field requiring quantitative analysis of complex systems.

Final Study Recommendations:

1. Practice Regularly: Work through diverse problem types, including multiple choice, free response, and laboratory analysis questions.
2. Master the Fundamentals: Ensure solid understanding of the ideal gas law, first law of thermodynamics, and basic process types before tackling complex cycles.
3. Develop Diagram Skills: Practice sketching and interpreting P-V diagrams for different thermodynamic processes and cycles.
4. Connect to Real World: Look for thermodynamic principles in everyday experiences – car engines, refrigerators, weather patterns, and cooking processes.
5. Form Study Groups: Explaining thermodynamic concepts to classmates helps deepen your own understanding and reveals knowledge gaps.
6. Use Multiple Resources: Supplement this guide with textbook problems, online simulations, and laboratory experiences.
7. Time Management: Practice working problems under timed conditions to prepare for exam pressure.

With dedicated study and practice, you’ll develop the knowledge and skills needed to excel on the AP Physics 2 exam and gain a deep appreciation for one of physics’ most fundamental and useful areas. The principles you learn in thermodynamics will continue to inform your understanding of energy, efficiency, and the physical world throughout your scientific career.

Remember: thermodynamics isn’t just about passing an exam – it’s about understanding the fundamental rules that govern energy and entropy in our universe. These concepts connect the microscopic world of atoms and molecules to the macroscopic phenomena we observe daily, providing insights into everything from biological processes to stellar evolution. Master these principles, and you’ll have powerful tools for understanding and analyzing the physical world around you.

Recommended –

• AP Physics Syllabus & Exam Pattern 2025 | Grade 12 Physics USA Guide
• Master AP Physics 1 Unit 8: Fluids – The Complete Guide to Pressure, Buoyancy, and Flow