The Physics of Spinning Worlds
Every morning when you wake up, you’re already experiencing one of the most fundamental examples of rotational motion – our Earth spinning on its axis at over 1,000 mph at the equator. From the gyroscope in your smartphone that knows which way you’re holding it, to the massive turbines generating electricity in power plants, to the precise rotation of hard drives storing your data, rotational motion and the energy and momentum associated with it shape our technological world.
Yet many students find Unit 6 of AP Physics C: Mechanics particularly challenging. Why? Because rotational motion requires you to think in entirely new ways about familiar concepts like energy and momentum. Instead of linear velocity, we have angular velocity. Instead of mass, we consider moment of inertia. Instead of linear momentum, we work with angular momentum. But here’s the exciting part – the fundamental principles of conservation that govern linear motion apply beautifully to rotational systems, creating elegant parallels that, once understood, make complex problems surprisingly manageable.
This comprehensive guide will transform your understanding of rotational energy and momentum from confusion into confidence. You’ll discover why a figure skater spins faster when pulling in her arms, how engineers design flywheels to store enormous amounts of energy, and why a rolling ball has more kinetic energy than a sliding one. More importantly, you’ll master the problem-solving strategies that will help you excel on the AP Physics C exam.
Learning Objectives: What You’ll Master
By the end of this unit, aligned with College Board standards for AP Physics C: Mechanics, you will be able to:
Conceptual Understanding:
- Distinguish between rotational and translational kinetic energy in complex systems
- Explain the physical significance of moment of inertia and how mass distribution affects rotational motion
- Apply conservation of angular momentum to predict behavior in isolated systems
- Analyze the relationship between torque, angular impulse, and changes in angular momentum
- Understand rolling motion as a combination of translation and rotation
Mathematical Proficiency:
- Calculate moments of inertia for various geometric shapes and composite objects
- Solve energy conservation problems involving both rotational and translational motion
- Apply the parallel axis theorem to determine moments of inertia for displaced axes
- Use angular momentum conservation in collision and explosion problems
- Analyze rolling motion using energy and momentum principles
Experimental Skills:
- Design experiments to measure moment of inertia and verify theoretical predictions
- Analyze data from rotational motion experiments using graphical methods
- Apply uncertainty analysis to rotational measurements
- Connect laboratory observations to theoretical concepts
1. Fundamental Concepts: Building Your Rotational Intuition
The Rotational-Linear Analogy
Understanding rotational motion becomes much easier when you recognize the beautiful parallels between linear and rotational quantities. Just as Newton’s laws govern linear motion, analogous principles govern rotational motion.
In linear motion, we describe an object’s motion using position (x), velocity (v), and acceleration (a). In rotational motion, we use angular position (θ), angular velocity (ω), and angular acceleration (α). The relationships are remarkably similar:
For linear motion: v = dx/dt and a = dv/dt
For rotational motion: ω = dθ/dt and α = dω/dt
Real-World Physics: When you’re driving and turn the steering wheel, your hands trace a circular path. The faster you turn the wheel, the greater the angular velocity. If you need to turn more quickly – perhaps to avoid an obstacle – you increase the angular acceleration.
Moment of Inertia: The Rotational Mass
Perhaps the most crucial concept in rotational dynamics is moment of inertia (I), often called the “rotational mass.” But unlike mass, which is an intrinsic property of an object, moment of inertia depends not only on the object’s mass but also on how that mass is distributed relative to the axis of rotation.
Think about holding a baseball bat. If you grip it normally and try to swing it, you feel significant resistance to rotational motion. But if you grip it at the heavy end and try to rotate it around the handle, the resistance is much greater. The bat’s mass hasn’t changed, but its moment of inertia about different axes varies dramatically.
Physics Check: Why does a figure skater spin faster when pulling in her arms? Her angular momentum is conserved, but her moment of inertia decreases as she brings mass closer to her rotation axis, so her angular velocity must increase to compensate.
[EQUATION: I = Σmᵢrᵢ² for discrete point masses, or I = ∫r²dm for continuous mass distributions]
For common geometric shapes rotating about their center of mass:
- Solid cylinder: I = ½MR²
- Hollow cylinder: I = MR²
- Solid sphere: I = ⅖MR²
- Thin rod (about center): I = 1/12ML²
The Parallel Axis Theorem
When an object rotates about an axis that doesn’t pass through its center of mass, we use the parallel axis theorem to find its moment of inertia:
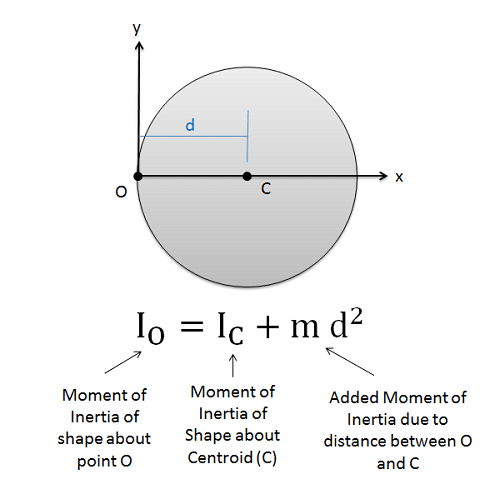
[EQUATION: I = Icm + Md²]
where Icm is the moment of inertia about the center of mass, M is the total mass, and d is the distance between the two parallel axes.
Problem-Solving Strategy: Always start with the center-of-mass moment of inertia from your reference sheet, then apply the parallel axis theorem if needed. This approach minimizes calculation errors and builds physical intuition.
2. Rotational Kinetic Energy: Energy in Motion
Understanding Rotational Kinetic Energy
Just as a moving object possesses kinetic energy due to its linear motion, a rotating object possesses rotational kinetic energy. The formula mirrors linear kinetic energy but uses rotational quantities:
[EQUATION: KErot = ½Iω²]
Compare this to linear kinetic energy: KElin = ½mv²
This parallel isn’t coincidental – both represent energy associated with motion, whether linear or rotational. For objects that both translate and rotate simultaneously (like a rolling ball), the total kinetic energy is the sum of both components:
[EQUATION: KEtotal = KEtranslational + KErotational = ½mv² + ½Iω²]
Rolling Motion: Translation Plus Rotation
Rolling motion presents one of the most elegant examples of combined translational and rotational motion. When a sphere rolls without slipping, there’s a beautiful constraint relationship between linear and angular velocity:
[EQUATION: v = ωR]
where v is the center-of-mass velocity, ω is the angular velocity, and R is the radius.

Real-World Physics: This relationship explains why larger wheels on vehicles provide better fuel efficiency at highway speeds. For the same angular velocity of the wheel, a larger radius results in higher linear velocity, meaning the engine doesn’t need to spin as fast to maintain speed.
Energy Conservation in Rolling Systems
Consider a solid sphere rolling down an inclined plane. Using energy conservation:
Initial energy = Final energy
mgh = ½mv² + ½Iω²
For a solid sphere, I = ⅖mR², and using the rolling constraint v = ωR:
mgh = ½mv² + ½(⅖mR²)(v/R)²
mgh = ½mv² + ⅕mv²
mgh = 7/10 mv²
Solving for velocity: v = √(10gh/7)
Common Error Alert: Students often forget that rolling objects have both translational and rotational kinetic energy. A rolling object will always be slower than a sliding object starting from the same height because some of the initial gravitational potential energy goes into rotational motion.
3. Angular Momentum: The Rotational Equivalent of Linear Momentum
Defining Angular Momentum
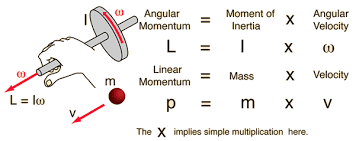
Angular momentum (L) is the rotational analog of linear momentum. For a rigid body rotating about a fixed axis:
[EQUATION: L = Iω]
Just as linear momentum equals mass times velocity (p = mv), angular momentum equals moment of inertia times angular velocity.
For point particles moving in circular paths:
[EQUATION: L = rmv⊥ = rp⊥]
where r is the distance from the axis of rotation and v⊥ is the component of velocity perpendicular to the radius vector.
Conservation of Angular Momentum
One of the most powerful principles in physics is conservation of angular momentum. In the absence of external torques, the total angular momentum of a system remains constant:
[EQUATION: L₁ = L₂, or I₁ω₁ = I₂ω₂]
This principle explains numerous phenomena, from the behavior of figure skaters to the formation of galaxies.
Real-World Physics: Earth’s rotation rate is gradually slowing due to tidal forces from the Moon. As Earth’s rotational period increases, the Moon moves farther away to conserve the total angular momentum of the Earth-Moon system. This effect can be measured with laser reflectors placed on the Moon by Apollo astronauts.
Angular Impulse and Momentum Change
Just as impulse changes linear momentum, angular impulse changes angular momentum:
[EQUATION: J = ∫τdt = ΔL = L₂ – L₁]
where τ is torque and J is angular impulse.
Problem-Solving Strategy: When analyzing rotational collisions or interactions, always check whether external torques are negligible. If so, angular momentum is conserved, which often provides the key relationship needed to solve the problem.
4. Mathematical Framework: Essential Equations and Derivations
Core Rotational Dynamics Equations
The fundamental equation relating torque to angular acceleration mirrors Newton’s second law:
[EQUATION: Στ = Iα]
This is the rotational version of ΣF = ma. Just as force causes linear acceleration, torque causes angular acceleration.
For rotational work and power:
[EQUATION: W = ∫τdθ]
[EQUATION: P = τω]
These relationships parallel their linear counterparts (W = ∫F·dx and P = F·v).
Deriving the Rolling Constraint
When an object rolls without slipping, the contact point has zero velocity relative to the surface. This constraint leads to the fundamental rolling relationship.
Consider a wheel of radius R rolling distance s. The wheel rotates through angle θ = s/R. Taking the time derivative:
dθ/dt = (1/R)(ds/dt)
ω = v/R
Therefore: v = ωR
This constraint is crucial for solving rolling motion problems correctly.
Energy Methods in Rotational Systems
Energy conservation provides powerful problem-solving tools for rotational systems. The general energy conservation equation for systems with both translational and rotational motion is:
[EQUATION: E₁ = E₂]
[EQUATION: (KE₁ + PE₁) = (KE₂ + PE₂)]
[EQUATION: (½mv₁² + ½Iω₁² + mgh₁) = (½mv₂² + ½Iω₂² + mgh₂)]
Physics Check: Always verify that your final answer makes physical sense. For example, when an object rolls down an incline, it should have less speed at the bottom than if it had slid frictionlessly, because some energy goes into rotational motion.
5. Problem-Solving Strategies: Systematic Approaches
The Five-Step Method for Rotational Problems
- Identify the System and Constraints
- What objects are involved?
- Are there rolling constraints (v = ωR)?
- Is angular momentum conserved?
- Choose Your Approach
- Energy conservation for problems involving heights or speeds
- Angular momentum conservation for collisions and interactions
- Torque analysis for force and acceleration problems
- Set Up Equations Systematically
- Write conservation equations first
- Apply constraint equations
- Use kinematic relationships if needed
- Solve Algebraically Before Substituting Numbers
- Keep variables symbolic as long as possible
- Check units at each step
- Look for simplifications
- Verify Your Answer
- Do the units work out correctly?
- Is the magnitude reasonable?
- Does it satisfy limiting cases?
Common Problem Categories and Approaches
Rolling Down Inclines: Use energy conservation with the rolling constraint v = ωR. Remember that objects with smaller moments of inertia (relative to MR²) will accelerate faster down inclines.
Rotational Collisions: Apply conservation of angular momentum. Be careful about the axis of rotation – it should be the same before and after collision.
Compound Systems: For objects like yo-yos or pulleys with strings, use energy conservation and careful attention to constraint relationships between linear and angular motion.
Variable Moment of Inertia: When moment of inertia changes (like a figure skater pulling in arms), use conservation of angular momentum: I₁ω₁ = I₂ω₂.
6. Laboratory Applications: Connecting Theory to Experiment
Measuring Moment of Inertia Experimentally
One of the most important experimental skills in this unit is measuring moment of inertia and comparing results to theoretical predictions.
Method 1: Rotational Energy Approach
Release an object from rest at height h and measure its angular velocity ω at the bottom. Using energy conservation:
mgh = ½mv² + ½Iω²
With the rolling constraint v = ωR:
I = (2gh/ω²) – mR²
Method 2: Oscillation Method
For objects that can oscillate about an axis, the period of small oscillations is:
T = 2π√(I/mgd)
where d is the distance from the axis to the center of mass. Measure T and solve for I.
Experimental Design Considerations
Controlling Variables: When investigating how mass distribution affects moment of inertia, keep total mass constant while changing the distribution. Ring-and-disk systems work well for this.
Minimizing Systematic Errors: Rolling friction, air resistance, and string stretching can affect results. Use smooth surfaces, massive objects (to minimize air resistance effects), and inextensible strings.
Data Analysis Techniques: Plot results to check for linear relationships. For example, plotting I vs. (mass × radius²) should give a straight line for objects of similar shape but different sizes.
7. Advanced Applications: Real-World Engineering and Physics
Flywheel Energy Storage Systems
Modern technology increasingly uses flywheel systems to store energy efficiently. These systems spin massive disks at extremely high speeds, storing energy as rotational kinetic energy.
The energy stored in a flywheel is:
[EQUATION: E = ½Iω²]
To maximize energy storage while minimizing mass, engineers design flywheels with most mass concentrated at large radii. For a thin ring of mass M and radius R:
E = ½MR²ω² = ½M(ωR)²
This shows that both radius and angular velocity are crucial for energy storage.
Real-World Physics: Modern flywheel systems can store several kilowatt-hours of energy and provide power for minutes during electrical grid fluctuations. Some experimental transit systems use flywheel buses that capture energy during braking and release it during acceleration.
Gyroscopic Effects in Technology
Gyroscopes rely on conservation of angular momentum to maintain orientation. When you try to change the orientation of a spinning gyroscope, it precesses rather than rotating in the expected direction.
Real-World Physics: Your smartphone contains tiny MEMS (micro-electromechanical systems) gyroscopes that detect rotation in three dimensions. These devices enable features like screen rotation, camera stabilization, and motion-controlled games.
Planetary Motion and Angular Momentum
Kepler’s second law – that planets sweep out equal areas in equal times – is actually a statement about conservation of angular momentum. As a planet’s orbital radius changes, its speed changes to conserve angular momentum:
L = rmv = constant
This principle also explains why comets move much faster when close to the Sun than when far away.
8. Practice Problems Section
Multiple Choice Questions
Problem 1: A solid sphere and a hollow sphere of the same mass and radius are released simultaneously from the top of an inclined plane. Which reaches the bottom first?
A) The solid sphere
B) The hollow sphere
C) They reach the bottom simultaneously
D) The answer depends on the angle of the incline
Solution: A) The solid sphere. Using energy conservation for rolling objects:
For the solid sphere: mgh = ½mv² + ½(⅖mR²)(v/R)² = 7/10 mv²
Therefore: v = √(10gh/7)
For the hollow sphere: mgh = ½mv² + ½(⅔mR²)(v/R)² = 5/6 mv²
Therefore: v = √(6gh/5)
Since 10/7 > 6/5, the solid sphere has greater speed and reaches the bottom first.
Problem 2: A figure skater is spinning with angular velocity ω₁ when she pulls her arms inward, reducing her moment of inertia from I₁ to I₂ = I₁/2. Her new angular velocity is:
A) ω₁/2
B) ω₁
C) √2 ω₁
D) 2ω₁
Solution: D) 2ω₁. Using conservation of angular momentum:
L₁ = L₂
I₁ω₁ = I₂ω₂
I₁ω₁ = (I₁/2)ω₂
ω₂ = 2ω₁
Free Response Problems
Problem 3: A uniform rod of length L and mass M is pivoted about one end and released from rest in a horizontal position. Find the angular velocity of the rod when it reaches the vertical position.
Solution:
Step 1: Identify the system and approach
- Rod rotating about one end
- Use energy conservation
- Moment of inertia about end: I = ⅓ML²
Step 2: Set up energy conservation
Initial energy = Final energy
PEᵢ + KEᵢ = PEf + KEf
Step 3: Define energy terms
- Initial PE: Mg(L/2) (center of mass at L/2 from pivot)
- Initial KE: 0 (starts from rest)
- Final PE: 0 (taking vertical position as reference)
- Final KE: ½Iω²
Step 4: Apply conservation
Mg(L/2) = ½(⅓ML²)ω²
MgL/2 = ML²ω²/6
3g/L = ω²
ω = √(3g/L)
Problem 4: A solid cylinder of mass M and radius R rolls without slipping down an inclined plane of height h and angle θ. At the bottom, it encounters a rough horizontal surface with coefficient of kinetic friction μₖ. How far does the cylinder slide before coming to rest?
Solution:
Step 1: Find velocity at bottom of incline using energy conservation
mgh = ½mv² + ½Iω²
mgh = ½mv² + ½(½MR²)(v/R)²
mgh = ½mv² + ¼mv²
mgh = ¾mv²
v = √(4gh/3)
Step 2: Analyze motion on horizontal surface
Initial KE = Work done against friction
¾Mv² = μₖMg·d
where d is the sliding distance.
Step 3: Solve for sliding distance
d = 3v²/(4μₖg) = 3(4gh/3)/(4μₖg) = h/μₖ
The sliding distance equals the original height divided by the coefficient of friction.
Problem 5: Two uniform disks with the same radius R but masses M₁ = 2M and M₂ = M are initially spinning with angular velocities ω₁ = ω and ω₂ = -2ω (opposite directions). They are brought into contact and friction causes them to reach the same final angular velocity. Find the final angular velocity and the energy lost during this process.
Solution:
Step 1: Apply conservation of angular momentum
Initial: L₁ = I₁ω₁ + I₂ω₂ = (½·2M·R²)(ω) + (½·M·R²)(-2ω)
L₁ = MR²ω – MR²ω = 0
Final: L₂ = (I₁ + I₂)ωf = (MR² + ½MR²)ωf = 3/2 MR²ωf
Step 2: Solve for final angular velocity
L₁ = L₂
0 = 3/2 MR²ωf
ωf = 0
Step 3: Calculate energy lost
Initial KE: KEᵢ = ½I₁ω₁² + ½I₂ω₂²
KEᵢ = ½(MR²)ω² + ½(½MR²)(4ω²) = ½MR²ω² + MR²ω² = 3/2 MR²ω²
Final KE: KEf = 0 (since ωf = 0)
Energy lost: ΔE = KEᵢ – KEf = 3/2 MR²ω²
Experimental Design Questions
Problem 6: Design an experiment to verify that the moment of inertia of a uniform rod about its center is I = 1/12 ML².
Experimental Design:
- Setup: Mount the rod horizontally on a low-friction bearing at its center. Attach a small mass m to one end of the rod at distance L/2 from the center.
- Procedure:
- Displace the rod slightly from equilibrium and release
- Measure the period T of small oscillations
- The system acts as a physical pendulum with moment of inertia Itotal = Irod + m(L/2)²
- Analysis:
For a physical pendulum: T = 2π√(I/(mgd))
where d = L/2 is the distance from axis to center of mass of the added mass T = 2π√([Irod + m(L/2)²]/(mg·L/2)) Solving for Irod:
Irod = m(L/2)²[(T/2π)²(gL/2) – 1] - Verification: Calculate the theoretical value (1/12 ML²) and compare with experimental result.
9. Common Misconceptions and Error Prevention
Misconception 1: Confusing Linear and Angular Quantities
Common Error: Using F = ma for rotational motion instead of τ = Iα.
Prevention Strategy: Always identify whether the problem involves linear motion, rotational motion, or both. Make a clear list of relevant quantities and their units before starting calculations.
Misconception 2: Forgetting the Rolling Constraint
Common Error: In rolling problems, treating translational and rotational motion as independent.
Prevention Strategy: Immediately write v = ωR whenever you see “rolling without slipping.” This constraint relationship is usually the key to solving the problem correctly.
Misconception 3: Incorrect Moment of Inertia Calculations
Common Error: Using the wrong moment of inertia formula or forgetting to apply the parallel axis theorem when needed.
Prevention Strategy: Always start by identifying the axis of rotation clearly. Use your reference sheet for standard moments of inertia, and remember to apply the parallel axis theorem when the rotation axis doesn’t pass through the center of mass.
Misconception 4: Energy Conservation Errors in Rolling Motion
Common Error: Forgetting that rolling objects have both translational and rotational kinetic energy.
Prevention Strategy: For any rolling object, always write KEtotal = ½mv² + ½Iω² and use the constraint v = ωR to eliminate one variable.
Common Error Alert: Students often think that all objects roll down inclines at the same rate, like objects sliding down frictionless inclines. This is incorrect – objects with different moments of inertia will have different accelerations down inclines.
10. Advanced Problem-Solving Techniques
Using Energy Methods Effectively
Energy conservation is often the most elegant approach to rotational problems, but it requires careful setup:
- Identify all forms of energy in initial and final states
- Choose your reference levels for potential energy carefully
- Include both translational and rotational kinetic energy for rolling objects
- Apply constraints like v = ωR to reduce the number of variables
Angular Momentum Conservation Strategy
When applying conservation of angular momentum:
- Choose your axis carefully – it should be the same for initial and final states
- Check for external torques – conservation only applies when Στext = 0
- Include all objects that might have angular momentum about the chosen axis
- Be careful with signs – establish a positive direction and stick to it
Dealing with Variable Moments of Inertia
Some problems involve changing mass distributions (like figure skaters or collapsing stars):
- Use conservation of angular momentum: I₁ω₁ = I₂ω₂
- Calculate the change in rotational kinetic energy: ΔKE = ½I₂ω₂² – ½I₁ω₁²
- Remember that energy is usually not conserved when internal forces change the mass distribution
11. Connections to Other AP Physics Topics
Links to Linear Momentum and Collisions
The principles you learned about conservation of linear momentum in collisions apply directly to rotational systems. Just as linear momentum is conserved in the absence of external forces, angular momentum is conserved in the absence of external torques.
Connections to Simple Harmonic Motion
Physical pendulums represent a beautiful connection between rotational dynamics and oscillatory motion. The restoring torque for small angles is proportional to the angular displacement, leading to simple harmonic motion with period T = 2π√(I/(mgd)).
Relationship to Gravitation
Kepler’s laws of planetary motion are fundamentally about conservation of angular momentum. As planets orbit the Sun, they speed up when closer (smaller r) and slow down when farther (larger r) to conserve angular momentum L = rmv.
Exam Preparation Strategies
What the AP Physics C Exam Emphasizes
The College Board consistently tests certain concepts more heavily than others in Unit 6:
Heavily Tested Topics:
- Rolling motion problems (nearly every exam)
- Conservation of angular momentum in collisions
- Energy conservation with both translation and rotation
- Moment of inertia calculations and the parallel axis theorem
Moderately Tested Topics:
- Angular impulse and momentum change
- Rotational dynamics with Newton’s second law (τ = Iα)
- Physical pendulums and oscillations
Lightly Tested Topics:
- Detailed gyroscopic effects
- Complex multi-body systems
Effective Study Strategies
Two Weeks Before the Exam:
- Review all major concepts and ensure you understand the physics, not just the math
- Practice drawing free-body diagrams for rotating systems
- Make sure you can quickly recall moments of inertia for common shapes
One Week Before:
- Focus on practice problems, especially rolling motion and conservation problems
- Time yourself on free-response questions (should complete in 15-25 minutes each)
- Review common mistakes and make sure you’re not repeating them
Day Before:
- Review your formula sheet and make sure you understand when to use each equation
- Practice a few quick problems to stay sharp, but don’t cram new material
- Get a good night’s sleep – physics problems require clear thinking
Problem-Solving Time Management
Multiple Choice Strategy:
- Spend no more than 90 seconds per problem on average
- If a calculation is getting complicated, look for shortcuts or limiting cases
- Use dimensional analysis to eliminate obviously wrong answers quickly
- Trust your physics intuition for qualitative questions
Free Response Strategy:
- Read the entire problem before starting and plan your approach
- Show your work clearly – partial credit is awarded for correct physics reasoning
- Start with basic principles (energy conservation, momentum conservation, etc.)
- Check your answers for reasonableness – wildly inappropriate numbers suggest errors
12. Technology and Modern Applications
Rotational Motion in Modern Technology
Electric Motors and Generators: These devices convert between electrical and mechanical energy through rotational motion. The torque produced by a motor is proportional to the current, while the voltage generated by a generator is proportional to the angular velocity.
Hard Drives and Data Storage: Traditional hard drives store information on spinning disks. The angular momentum of these disks creates gyroscopic effects that can affect laptop orientation. Modern solid-state drives eliminate these effects entirely.
Wind Turbines: These massive systems convert wind energy into electrical energy through rotation. The moment of inertia of the blades affects how quickly they respond to changes in wind speed, influencing both efficiency and structural stress.
Aerospace Applications
Satellite Attitude Control: Spacecraft use reaction wheels (essentially flywheels) to control their orientation without using fuel. By spinning up wheels in different directions, satellites can rotate precisely for communications, observations, or solar panel alignment.
Gyroscopic Stabilization: From motorcycle stability to ship stabilizers to the International Space Station, gyroscopic effects provide stability and control in countless applications.
Emerging Technologies
Flywheel Energy Storage: As renewable energy sources become more common, flywheel systems provide clean, efficient energy storage with rapid charge and discharge capabilities.
Quantum Angular Momentum: At the atomic scale, quantum mechanical spin represents intrinsic angular momentum that doesn’t correspond to classical rotation but follows the same conservation laws.
Conclusion and Next Steps
Mastering the energy and momentum of rotating systems represents a significant milestone in your physics education. You’ve learned to think about motion in entirely new ways, discovering that the elegant principles governing linear motion extend beautifully into the rotational domain. The conservation laws you’ve studied – particularly conservation of energy and angular momentum – are among the most powerful tools in all of physics.
As you prepare for the AP Physics C exam, remember that success comes from understanding the underlying physics, not just memorizing formulas. Practice visualizing problems, drawing clear diagrams, and always checking whether your answers make physical sense. The problem-solving strategies you’ve developed here will serve you well not only on the exam but throughout any future studies in physics and engineering.
Looking Ahead: Advanced Topics
The concepts you’ve mastered form the foundation for numerous advanced topics:
University Physics: You’ll extend these ideas to three-dimensional rotations, rigid body dynamics, and more complex systems involving both translation and rotation.
Engineering Applications: Mechanical engineers use these principles to design everything from car engines to industrial machinery to robotic systems.
Astrophysics: The rotation of stars, planets, and galaxies all follow the principles you’ve learned, but on scales that reveal additional physics like general relativity.
Quantum Mechanics: Angular momentum becomes quantized at the atomic scale, but the conservation laws remain fundamental to understanding atomic and molecular physics.
Final Exam Strategy Reminders
- Master the fundamentals: Know your moment of inertia formulas cold, understand when angular momentum is conserved, and always remember to include both forms of kinetic energy for rolling objects.
- Practice systematically: Work through problems step-by-step using the five-step method outlined in this guide. Don’t skip steps even when problems seem simple.
- Check your physics intuition: If an answer doesn’t make physical sense, investigate. Often, calculation errors reveal themselves through unreasonable results.
- Stay confident: You’ve learned some of the most beautiful and powerful concepts in classical physics. Trust your preparation and approach each problem methodically.
The journey through rotational energy and momentum has equipped you with tools to understand and analyze the spinning world around you – from the quantum scale to the cosmic scale. Whether you’re bound for engineering, physics, or any field that values analytical thinking, these concepts will continue to serve you throughout your academic and professional career.
Remember: physics is not about memorizing formulas – it’s about understanding how the universe works. The elegant mathematics you’ve learned here describes real phenomena that shape everything from the device you’re reading this on to the galaxy containing our solar system. That’s the true power and beauty of physics, and you’re now equipped to appreciate and apply it.
Success on the AP Physics C exam is within your reach. You have the knowledge, you have the tools, and you have the strategies. Now go demonstrate your mastery of these fundamental concepts that govern our rotating universe.
Recommended –

