The Invisible Symphony Around You
Right now, as you read this guide, you’re surrounded by an invisible symphony of electromagnetic waves. Your smartphone receives radio waves from cell towers, WiFi signals bounce around your room, light waves illuminate the page, and even the warmth you feel from the sun comes from infrared electromagnetic radiation. Every time you use GPS, watch television, or heat food in a microwave, you’re experiencing the practical applications of electromagnetic wave theory.
This chapter represents one of the most elegant achievements in physics – James Clerk Maxwell’s unification of electricity and magnetism into a single electromagnetic field theory. What makes this topic particularly fascinating is how Maxwell predicted the existence of electromagnetic waves purely through mathematical equations, and Heinrich Hertz later confirmed them experimentally. This discovery revolutionized our understanding of light and laid the foundation for modern communication technology.
Understanding electromagnetic waves isn’t just about passing your CBSE exam – it’s about grasping the fundamental principles that power our digital world. From the 5G networks connecting our devices to the medical imaging technologies saving lives, electromagnetic wave theory touches every aspect of modern civilization.
Learning Objectives
By mastering this chapter, you’ll be able to:
- Understand Maxwell’s equations and their physical significance in predicting electromagnetic waves
- Analyze the relationship between oscillating electric and magnetic fields in wave propagation
- Calculate wave parameters like frequency, wavelength, and speed for different electromagnetic radiations
- Explain the electromagnetic spectrum and applications of different frequency ranges
- Solve problems involving energy and momentum transport by electromagnetic waves
- Apply wave theory to real-world technologies and natural phenomena
- Design experiments to demonstrate electromagnetic wave properties
- Connect electromagnetic theory to modern communication systems and medical applications
1. The Genesis of Electromagnetic Wave Theory
Maxwell’s Revolutionary Insight
Before Maxwell, electricity and magnetism were considered separate phenomena. Scientists knew that moving charges created magnetic fields, and changing magnetic fields could induce electric fields, but the complete picture remained elusive. Maxwell’s genius lay in recognizing that Ampère’s law needed modification to maintain consistency with charge conservation.
Physics Check: Can you explain why a steady current through a capacitor seems impossible, yet AC circuits with capacitors work perfectly? The answer lies in Maxwell’s displacement current concept.
Maxwell introduced the concept of displacement current, which occurs when the electric field between capacitor plates changes over time. This seemingly abstract mathematical correction had profound physical implications – it completed the symmetry between electricity and magnetism and predicted the existence of electromagnetic waves.
[EQUATION: Maxwell’s Displacement Current: Id = ε₀(dΦE/dt), where ε₀ is the permittivity of free space and dΦE/dt represents the rate of change of electric flux]
The four Maxwell equations in their complete form are:
- Gauss’s Law: ∇·E = ρ/ε₀ (Electric fields originate from charges)
- Gauss’s Law for Magnetism: ∇·B = 0 (No magnetic monopoles exist)
- Faraday’s Law: ∇×E = -∂B/∂t (Changing magnetic fields create electric fields)
- Ampère-Maxwell Law: ∇×B = μ₀J + μ₀ε₀(∂E/∂t) (Currents and changing electric fields create magnetic fields)
Real-World Physics: GPS satellites must account for both special and general relativistic effects, but the fundamental electromagnetic wave propagation follows Maxwell’s classical theory with remarkable precision across the 20,000-kilometer journey from satellite to your phone.
The Wave Equation Emerges
When Maxwell manipulated his equations mathematically, he discovered that electric and magnetic fields could propagate as waves through empty space. The wave equation that emerges from Maxwell’s equations is:
[EQUATION: ∂²E/∂x² = μ₀ε₀(∂²E/∂t²) and ∂²B/∂x² = μ₀ε₀(∂²B/∂t²)]
This reveals that electromagnetic disturbances travel at speed c = 1/√(μ₀ε₀) ≈ 3.00 × 10⁸ m/s – exactly the measured speed of light! This wasn’t coincidence; Maxwell realized that light itself is an electromagnetic wave.
2. The Anatomy of Electromagnetic Waves
Wave Structure and Propagation
Electromagnetic waves consist of oscillating electric and magnetic fields that are perpendicular to each other and to the direction of wave propagation. This creates a transverse wave pattern where energy flows in the direction perpendicular to both field oscillations.
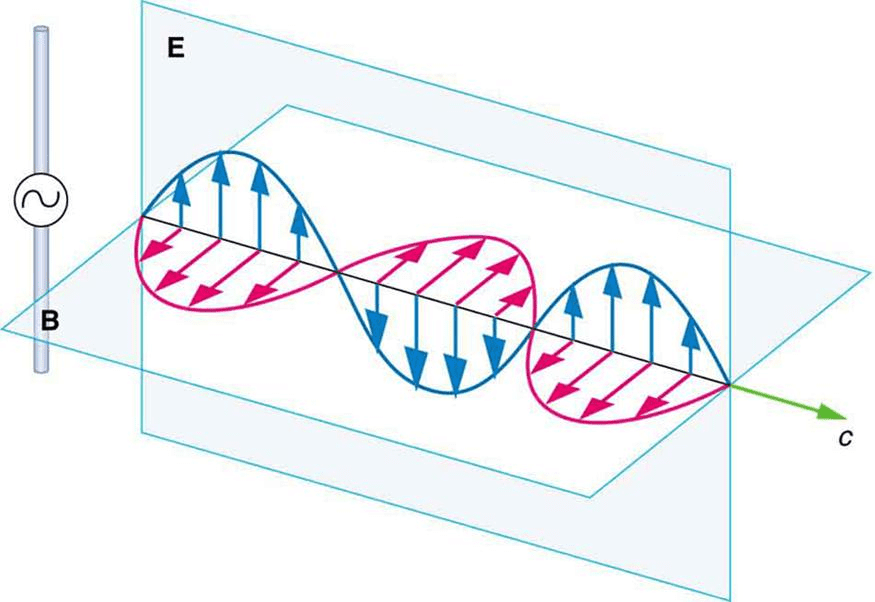
Key characteristics of electromagnetic waves include:
Mutual Perpendicularity: The electric field E, magnetic field B, and propagation direction k form a right-handed coordinate system. If you point your right thumb in the direction of E and curl your fingers toward B, your palm faces the propagation direction.
Phase Relationship: Electric and magnetic fields oscillate in phase – when one reaches maximum, so does the other. This synchronization is crucial for energy transport.
Field Magnitude Relationship: The ratio of electric to magnetic field amplitudes is constant: |E|/|B| = c = 3.00 × 10⁸ m/s
[EQUATION: E = cB, where c is the speed of light in vacuum]
Mathematical Description
For a plane electromagnetic wave propagating in the +x direction:
[EQUATION: E(x,t) = E₀sin(kx – ωt + φ) ĵ] [EQUATION: B(x,t) = B₀sin(kx – ωt + φ) k̂]
Where:
- E₀ and B₀ are the amplitude of electric and magnetic fields respectively
- k = 2π/λ is the wave number
- ω = 2πf is the angular frequency
- φ is the phase constant
- The relationship E₀ = cB₀ must hold
Problem-Solving Strategy: When analyzing electromagnetic wave problems, always verify that E⊥B, both fields are perpendicular to propagation direction, and |E|/|B| = c. These constraints often provide the key to solving complex problems.
Wave Properties in Different Media
When electromagnetic waves enter different materials, their speed changes according to:
[EQUATION: v = c/n, where n = √(εᵣμᵣ) is the refractive index]
For most non-magnetic materials, μᵣ ≈ 1, so n ≈ √εᵣ. The frequency remains constant while wavelength adjusts: λ_medium = λ_vacuum/n.
Common Error Alert: Students often confuse the speed of electromagnetic waves in materials with the drift velocity of charges in conductors. Electromagnetic waves travel at v = c/n even through materials containing slow-moving charges.
3. The Electromagnetic Spectrum: Nature’s Rainbow of Energy
Frequency and Energy Relationships
The electromagnetic spectrum spans an enormous range of frequencies, from extremely low-frequency radio waves to ultra-high-energy gamma rays. Each region has distinct properties and applications based on photon energy:
[EQUATION: E = hf = hc/λ, where h = 6.626 × 10⁻³⁴ J·s is Planck’s constant]
This relationship explains why different electromagnetic radiations interact differently with matter – higher frequency means higher photon energy and greater ability to cause atomic transitions or molecular changes.
Spectrum Regions and Applications
Radio Waves (f < 3 × 10⁹ Hz):
- Long-range communication due to low atmospheric absorption
- AM radio (535-1605 kHz), FM radio (88-108 MHz), TV broadcasts
- Wavelengths from kilometers to centimeters
- Low photon energies (10⁻⁹ to 10⁻⁶ eV) – insufficient to ionize atoms
Microwaves (3 × 10⁹ – 3 × 10¹² Hz):
- Satellite communication, GPS, radar systems
- Microwave ovens operate at 2.45 GHz to excite water molecule rotations
- Cosmic microwave background radiation provides evidence for Big Bang theory
- Wavelengths from 30 cm to 0.1 mm
Real-World Physics: Your microwave oven frequency (2.45 GHz) was chosen because it’s absorbed efficiently by water molecules, lies in an ISM (Industrial, Scientific, Medical) band to avoid interference with communication systems, and penetrates food deeply enough for even heating.
Infrared Radiation (3 × 10¹² – 4 × 10¹⁴ Hz):
- Thermal imaging and night vision technology
- Fiber optic communication uses near-infrared (800-1600 nm)
- Greenhouse effect – atmospheric CO₂ and H₂O absorb infrared
- Medical applications in physiotherapy and non-invasive diagnostics
Visible Light (4 × 10¹⁴ – 8 × 10¹⁴ Hz):
- Human vision evolved to utilize this “atmospheric window”
- Colors correspond to specific wavelengths: red (700 nm) to violet (400 nm)
- Photosynthesis harnesses visible light energy for biological processes
- LED technology revolutionizes efficient lighting
Ultraviolet Radiation (8 × 10¹⁴ – 3 × 10¹⁶ Hz):
- UV-A (315-400 nm): Tanning, phototherapy
- UV-B (280-315 nm): Vitamin D synthesis, sunburn
- UV-C (200-280 nm): Sterilization, ozone layer absorption
- Sufficient energy to break chemical bonds and cause DNA damage
X-rays (3 × 10¹⁶ – 3 × 10¹⁹ Hz):
- Medical imaging exploits differential absorption by bones vs. soft tissue
- Industrial non-destructive testing
- Astronomy – X-ray telescopes reveal high-energy cosmic phenomena
- Security scanners in airports
Gamma Rays (f > 3 × 10¹⁹ Hz):
- Nuclear medicine for cancer treatment
- Radioactive decay signatures
- Cosmic ray interactions in atmosphere
- Extremely high penetrating power requires heavy shielding
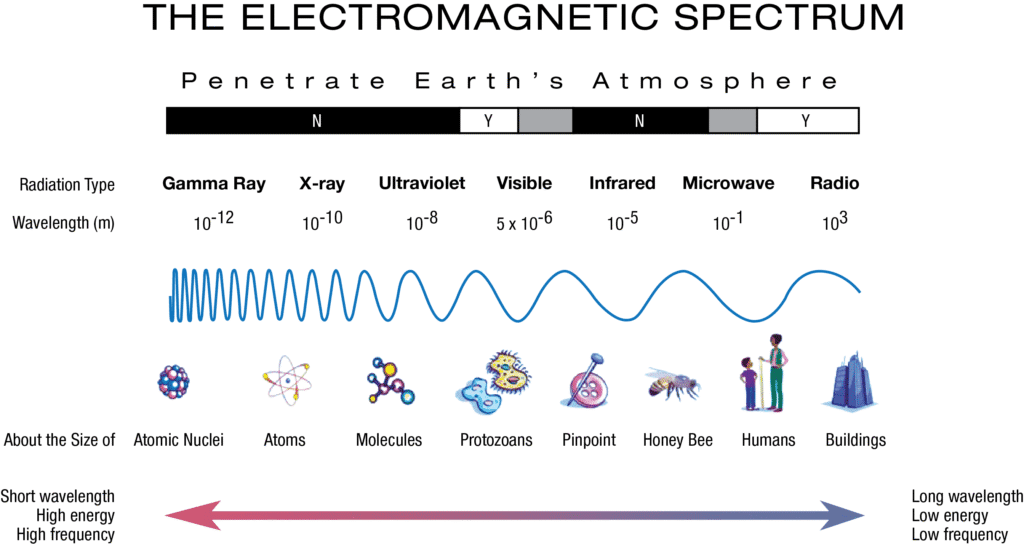
Atmospheric Interactions
Earth’s atmosphere creates “windows” and “barriers” for different electromagnetic frequencies:
Atmospheric Windows: Radio waves, visible light, and some infrared pass through with minimal absorption, enabling ground-based astronomy and communication.
Atmospheric Barriers: Most UV, X-rays, and gamma rays are absorbed, protecting life but requiring space-based telescopes for astronomical observations.
Physics Check: Why do we need the Hubble Space Telescope for UV astronomy but not for visible light observations? The ozone layer absorbs most UV radiation, preventing it from reaching ground-based telescopes.
4. Energy and Momentum in Electromagnetic Waves
Energy Density and Flow
Electromagnetic waves transport energy through space without requiring any material medium. The energy density (energy per unit volume) in an electromagnetic wave involves both electric and magnetic field contributions:
[EQUATION: Energy density u = uₑ + uᵦ = ½ε₀E² + (1/2μ₀)B²]
For electromagnetic waves in vacuum, the electric and magnetic energy densities are equal: uₑ = uᵦ = ¼ε₀E² = u/2
Total energy density: u = ½ε₀E² = ½ε₀E₀²sin²(kx – ωt + φ)
The time-averaged energy density becomes: ⟨u⟩ = ¼ε₀E₀² = ¼ε₀c²B₀²
Intensity and the Poynting Vector
The intensity I of an electromagnetic wave represents the average power per unit area transported by the wave. This is described by the Poynting vector:
[EQUATION: S⃗ = (1/μ₀)(E⃗ × B⃗)]
The magnitude gives the instantaneous power per unit area, while its direction indicates energy flow direction.
For a plane wave: |S| = |E||B|/μ₀ = E²/(μ₀c) = cε₀E²
Time-averaged intensity: I = ⟨|S|⟩ = ½cε₀E₀² = ½√(ε₀/μ₀)E₀²
[EQUATION: I = ½cε₀E₀² = cε₀E²ᵣₘₛ, where Eᵣₘₛ = E₀/√2]
Problem-Solving Strategy: When calculating electromagnetic wave intensity, remember that intensity depends on the square of field amplitude. Doubling the field amplitude quadruples the intensity – this relationship appears frequently in CBSE exam problems.
Radiation Pressure and Momentum
Electromagnetic waves carry momentum even though they have no rest mass. This momentum leads to radiation pressure when waves interact with matter:
[EQUATION: Momentum density = u/c = Energy density/c]
For complete absorption: Pᵣₐd = I/c For complete reflection: Pᵣₐd = 2I/c
The factor of 2 for reflection occurs because the wave momentum changes from +p to -p, creating a momentum change of 2p.
Real-World Physics: Solar sails for spacecraft propulsion utilize radiation pressure from sunlight. Although the force is tiny (about 9 × 10⁻⁶ N/m² at Earth’s distance from the Sun), it provides continuous acceleration without fuel consumption for interplanetary missions.
Worked Example: Solar Power Calculation
Problem: A solar panel with area 2.0 m² receives sunlight with intensity 1000 W/m². If the panel converts 20% of incident electromagnetic energy to electrical energy, calculate: (a) the electrical power output, (b) the radiation pressure on the panel, and (c) the electric field amplitude in the sunlight.
Solution:
(a) Electrical power output: Incident power = I × A = 1000 W/m² × 2.0 m² = 2000 W Electrical power = 0.20 × 2000 W = 400 W
(b) Radiation pressure: Assuming the panel absorbs most light (minimal reflection): Pᵣₐd = I/c = 1000 W/m² ÷ (3.00 × 10⁸ m/s) = 3.33 × 10⁻⁶ Pa
(c) Electric field amplitude: From I = ½cε₀E₀²: E₀² = 2I/(cε₀) = 2 × 1000/[(3.00 × 10⁸)(8.85 × 10⁻¹²)] E₀² = 7.52 × 10⁵ E₀ = 867 V/m
Check: Verify using B₀ = E₀/c = 867/(3.00 × 10⁸) = 2.89 × 10⁻⁶ T This gives reasonable field magnitudes for sunlight.
5. Wave Propagation and Polarization
Polarization Fundamentals
Electromagnetic waves can be polarized because they are transverse waves. Polarization describes the orientation of the electric field vector as the wave propagates. Understanding polarization is crucial for applications from LCD displays to radio astronomy.
Linear Polarization: The electric field oscillates in a single plane. Most common example is light from a polarizing filter.
Circular Polarization: The electric field vector rotates with constant magnitude as the wave propagates. GPS satellites transmit circularly polarized signals to maintain signal strength regardless of receiver orientation.
Elliptical Polarization: General case where the electric field traces an ellipse. Most real-world electromagnetic waves have elliptical polarization.
Mathematical Description of Polarization
For a wave propagating in the +z direction, we can write: [EQUATION: E⃗(z,t) = Eₓsin(kz – ωt + φₓ)x̂ + Eᵧsin(kz – ωt + φᵧ)ŷ]
The phase difference δ = φᵧ – φₓ determines the polarization type:
- δ = 0: Linear polarization
- δ = ±π/2 with Eₓ = Eᵧ: Circular polarization
- Other cases: Elliptical polarization
Malus’s Law and Polarization Applications
When polarized light passes through a polarizing filter (analyzer), the transmitted intensity follows Malus’s Law:
[EQUATION: I = I₀cos²θ]
Where θ is the angle between the incident polarization direction and the analyzer’s transmission axis.
Physics Check: Why do polarized sunglasses reduce glare from water surfaces? Reflected light becomes partially linearly polarized, and sunglasses are oriented to block this polarization direction.
Real-World Physics: LCD displays work by controlling liquid crystal molecular orientation to rotate light polarization. Pixels appear bright when polarization aligns with the final polarizer, and dark when polarization is perpendicular.
6. Electromagnetic Wave Generation and Detection
Accelerating Charges as Wave Sources
The fundamental principle of electromagnetic wave generation is that accelerating electric charges radiate electromagnetic energy. This connects microscopic atomic processes to macroscopic wave phenomena.
Larmor Formula: The power radiated by a non-relativistic accelerating point charge is: [EQUATION: P = (μ₀q²a²)/(6πc) = (q²a²)/(6πε₀c³)]
Where q is the charge and a is the acceleration magnitude.
Antenna Theory and Communication
Dipole Antennas: Half-wave dipole antennas (length λ/2) are most efficient for radio transmission and reception. The oscillating current creates time-varying electric and magnetic fields that propagate as electromagnetic waves.
Antenna Gain: Directional antennas focus electromagnetic energy in specific directions, increasing effective radiated power and reception sensitivity.
Frequency Matching: Antenna dimensions must match the wavelength for efficient operation. This explains why AM radio antennas are much larger than cell phone antennas.
Detection Mechanisms
Photoelectric Effect: High-frequency electromagnetic waves (UV, X-ray, gamma) can eject electrons from materials, enabling detection through current measurement.
Thermal Detection: Infrared radiation causes temperature increases that can be measured with bolometers and thermocouples.
Coherent Detection: Radio receivers use electronic circuits to amplify and demodulate electromagnetic wave signals.
Historical Context: Heinrich Hertz’s 1886-1888 experiments used spark gaps as both electromagnetic wave generators and detectors, providing the first experimental confirmation of Maxwell’s theory and laying the groundwork for wireless communication.
7. Applications in Modern Technology
Communication Systems
Radio and Television Broadcasting: AM radio uses amplitude modulation where information is encoded in the wave amplitude variations. FM radio uses frequency modulation for better noise immunity and audio quality.
Cellular Networks: Modern 4G and 5G systems use sophisticated digital modulation schemes and multiple antenna technologies (MIMO) to achieve high data rates and reliable communication.
Satellite Communication: Geostationary satellites at 36,000 km altitude use microwave frequencies for global communication coverage. The 0.25-second round-trip delay is noticeable in international phone calls.
Medical Applications
X-ray Imaging: Different tissue densities absorb X-rays differently, creating contrast in medical images. Bones absorb more strongly than soft tissue due to higher atomic number elements (calcium, phosphorus).
MRI (Magnetic Resonance Imaging): Uses radio frequency electromagnetic waves to manipulate nuclear spins in strong magnetic fields, producing detailed soft tissue images without ionizing radiation.
Diathermy: High-frequency electromagnetic fields heat internal tissues for therapeutic purposes, using the body’s electrical conductivity.
Radar and Remote Sensing
Doppler Radar: Measures frequency shifts in reflected electromagnetic waves to determine target velocity. Weather radar uses this principle to track storm movement and precipitation intensity.
Synthetic Aperture Radar (SAR): Creates high-resolution images by processing electromagnetic wave reflections from moving platforms, enabling Earth observation through clouds.
GPS Technology: Uses precisely timed electromagnetic signals from multiple satellites to determine position through trilateration. Relativistic effects must be corrected for meter-level accuracy.
Common Error Alert: Students sometimes think GPS works by measuring signal strength, but it actually measures signal travel time from satellites with precisely synchronized atomic clocks.
8. Laboratory Investigations and Experiments
Measuring Electromagnetic Wave Properties
Speed of Light Measurement: Modern experiments use laser interferometry or time-of-flight measurements over known distances. Student laboratory versions might use rotating mirrors or electronic timing circuits.
Polarization Studies: Use polarizing filters and light sources to verify Malus’s Law and demonstrate polarization concepts. Liquid crystal displays provide interesting polarization demonstrations.
Microwave Experiments: Standing wave measurements in waveguides can determine wavelength and verify the relationship c = fλ. Microwave ovens with removed turntables create standing wave patterns in food.
Electromagnetic Spectrum Investigation
Infrared Detection: Thermal cameras or simple thermometers can detect infrared radiation from warm objects, demonstrating that heat transfer can occur through electromagnetic radiation.
UV Detection: Fluorescent materials and UV-sensitive papers respond to ultraviolet radiation, showing the invisible portion of the electromagnetic spectrum.
Radio Wave Reception: Simple crystal radio circuits demonstrate electromagnetic wave detection and demodulation without external power sources.
Data Analysis and Error Considerations
Systematic Errors: Instrument calibration, environmental factors (temperature, humidity), and interference from other electromagnetic sources can affect measurements.
Random Errors: Statistical analysis of repeated measurements helps quantify precision and confidence intervals.
Uncertainty Propagation: When calculating derived quantities like wave speed from frequency and wavelength measurements, uncertainties combine according to standard formulas.
Practice Problems Section
Multiple Choice Questions with Solutions
Question 1: An electromagnetic wave propagating in vacuum has an electric field amplitude of 300 V/m. The magnetic field amplitude is: (a) 1.0 × 10⁻⁶ T (b) 1.0 × 10⁻⁷ T (c) 1.0 × 10⁻⁸ T (d) 9.0 × 10⁻⁸ T
Solution: Using E₀ = cB₀, we get B₀ = E₀/c = 300/(3.0 × 10⁸) = 1.0 × 10⁻⁶ T Answer: (a)
Question 2: The intensity of sunlight at Earth’s surface is approximately 1000 W/m². The radiation pressure on a perfectly absorbing surface is: (a) 3.3 × 10⁻⁶ Pa (b) 3.3 × 10⁻⁷ Pa (c) 3.3 × 10⁻⁵ Pa (d) 3.3 × 10⁻⁴ Pa
Solution: For complete absorption, Pᵣₐd = I/c = 1000/(3.0 × 10⁸) = 3.33 × 10⁻⁶ Pa Answer: (a)
Question 3: Which electromagnetic wave has the highest frequency? (a) Radio waves (b) X-rays (c) Gamma rays (d) Infrared rays
Solution: In order of increasing frequency: Radio < Infrared < Visible < UV < X-rays < Gamma rays Answer: (c)
Question 4: The electric and magnetic fields in an electromagnetic wave are: (a) Parallel to each other and perpendicular to propagation direction (b) Perpendicular to each other and parallel to propagation direction (c) Perpendicular to each other and perpendicular to propagation direction (d) At 45° to each other
Solution: E and B are mutually perpendicular and both perpendicular to propagation direction. Answer: (c)
Question 5: When an electromagnetic wave enters a medium with refractive index n = 1.5, its speed becomes: (a) 1.5c (b) c/1.5 (c) c (d) 2.25c
Solution: Wave speed in medium: v = c/n = c/1.5 = 0.67c Answer: (b)
Free Response Problems with Complete Solutions
Problem 1: A radio station broadcasts at 100 MHz with a power of 50 kW.
(a) Calculate the wavelength of the radio waves in air. (b) At a distance of 10 km from the transmitter, calculate the intensity of the radio waves assuming uniform radiation in all directions. (c) Find the electric and magnetic field amplitudes at this distance.
Solution:
(a) Wavelength calculation: λ = c/f = (3.00 × 10⁸ m/s)/(100 × 10⁶ Hz) = 3.0 m
(b) Intensity at 10 km: Assuming uniform spherical radiation: I = P/(4πr²) = 50,000 W/[4π(10,000 m)²] = 3.98 × 10⁻⁵ W/m²
(c) Field amplitudes: From I = ½cε₀E₀²: E₀² = 2I/(cε₀) = 2(3.98 × 10⁻⁵)/[(3.00 × 10⁸)(8.85 × 10⁻¹²)] E₀ = 0.173 V/m
B₀ = E₀/c = 0.173/(3.00 × 10⁸) = 5.77 × 10⁻¹⁰ T
Problem 2: Light with intensity I₀ passes through two polarizing filters. The first filter is oriented at 30° to the initial polarization direction, and the second filter is at 60° to the first filter’s axis.
(a) Find the intensity after the first polarizer. (b) Find the final intensity after both polarizers. (c) What single polarizer angle would produce the same final intensity?
Solution:
(a) After first polarizer: I₁ = I₀cos²(30°) = I₀(√3/2)² = 0.75I₀
(b) After second polarizer: I₂ = I₁cos²(60°) = 0.75I₀(1/2)² = 0.1875I₀
(c) Single polarizer angle: I₂ = I₀cos²θ = 0.1875I₀ cos²θ = 0.1875 θ = 66.9°
Advanced Application Problems
Problem 3: A space-based solar power station collects sunlight with intensity 1.36 kW/m² using a circular collector of radius 1 km. The collected energy is converted to microwaves at 90% efficiency and transmitted to Earth.
(a) Calculate the total electromagnetic power collected. (b) Find the microwave power transmitted toward Earth. (c) If the microwave beam has a circular cross-section with radius 2 km when it reaches Earth, calculate the intensity at Earth’s surface. (d) Compare this intensity to typical microwave oven levels (≈1000 W/m²).
Solution:
(a) Power collected: Area = πr² = π(1000 m)² = 3.14 × 10⁶ m² P_collected = IA = (1360 W/m²)(3.14 × 10⁶ m²) = 4.27 × 10⁹ W = 4.27 GW
(b) Microwave power transmitted: P_transmitted = 0.90 × 4.27 GW = 3.84 GW
(c) Intensity at Earth: Earth beam area = π(2000 m)² = 1.26 × 10⁷ m² I_Earth = P_transmitted/A_Earth = (3.84 × 10⁹ W)/(1.26 × 10⁷ m²) = 305 W/m²
(d) Comparison: I_Earth/I_microwave = 305/1000 = 0.31 The space solar power intensity is about 31% of microwave oven levels – significant but potentially safe with proper safety protocols.
Experimental Design Questions
Problem 4: Design an experiment to measure the speed of electromagnetic waves using a microwave oven (with safety modifications).
Experimental Design:
Materials needed:
- Microwave oven with turntable removed
- Chocolate bar or marshmallows (to visualize standing waves)
- Ruler or measuring tape
- Microwave frequency specification (typically 2.45 GHz)
Procedure:
- Remove turntable to prevent rotation
- Place chocolate bar in oven and heat briefly (10-15 seconds)
- Observe melted spots – these occur at antinodes of standing wave pattern
- Measure distance between adjacent melted spots (this equals λ/2)
- Calculate wavelength: λ = 2 × (distance between spots)
- Use c = fλ to calculate speed
Expected Results:
- Frequency f = 2.45 × 10⁹ Hz
- Distance between spots ≈ 6 cm, so λ ≈ 12 cm = 0.12 m
- Calculated speed: c = (2.45 × 10⁹)(0.12) = 2.94 × 10⁸ m/s
Error Analysis:
- Measurement uncertainty in spot spacing (±1-2 mm)
- Microwave frequency tolerance (±1%)
- Standing wave pattern distortion from oven geometry
- Expected accuracy: ±5-10%
Safety Considerations:
- Never operate oven with door open
- Use minimal heating time to avoid burns
- Ensure proper oven ventilation
Exam Preparation Strategies
High-Yield Topics for CBSE Board Exams
Frequently Tested Concepts:
- Maxwell’s Displacement Current: Understand conceptually and mathematically. Be able to explain why it was necessary and how it led to electromagnetic wave prediction.
- Wave Speed Relationships: Master c = fλ in vacuum and v = c/n in materials. Practice unit conversions between different frequency/wavelength ranges.
- Energy and Intensity Calculations: Know the relationships between field amplitudes, intensity, and power. Practice problems involving solar radiation and electromagnetic energy transport.
- Electromagnetic Spectrum: Memorize approximate frequency/wavelength ranges for different regions. Understand applications and photon energy relationships.
- Polarization and Malus’s Law: Understand linear, circular, and elliptical polarization. Practice calculations with multiple polarizers.
Problem-Solving Methodology
Step 1: Identify Given Information and Target
- List known quantities with units
- Identify what needs to be calculated
- Note any constraints or special conditions
Step 2: Choose Relevant Principles
- Maxwell’s equations for fundamental relationships
- Wave equations for propagation problems
- Energy/intensity formulas for power calculations
- Spectrum properties for frequency/wavelength problems
Step 3: Set Up Equations Systematically
- Write key relationships first
- Substitute known values carefully
- Check units at each step
Step 4: Solve and Verify
- Perform calculations with appropriate significant figures
- Check that answer has correct units
- Verify reasonableness (order of magnitude, physical meaning)
Common Exam Mistakes and Prevention
Mistake 1: Confusing E and B field units
- Electric field: V/m or N/C
- Magnetic field: T (Tesla) or Wb/m²
- Prevention: Always write units explicitly in calculations
Mistake 2: Wrong speed in different media
- In vacuum: c = 3.00 × 10⁸ m/s
- In medium: v = c/n where n > 1 for most materials
- Prevention: Clearly identify the medium before using wave speed
Mistake 3: Polarization angle confusion
- Malus’s Law uses angle between polarization directions, not absolute angles
- Prevention: Draw diagrams showing polarization directions clearly
Mistake 4: Electromagnetic spectrum range errors
- Radio: longest wavelength, lowest frequency
- Gamma: shortest wavelength, highest frequency
- Prevention: Create a mental spectrum chart with key boundaries
Mistake 5: Energy and power unit confusion
- Energy: Joules (J)
- Power: Watts (W = J/s)
- Intensity: W/m²
- Prevention: Check that final units match the requested quantity
Time Management for CBSE Physics Exam
Electromagnetic Waves Questions (typically 3-5 marks):
- Read question carefully (30 seconds)
- Identify approach and write key equations (1 minute)
- Perform calculations (2-3 minutes)
- Check answer and units (30 seconds)
- Total time budget: 4-5 minutes per question
Strategy for Complex Problems:
- Start with straightforward parts first
- Use earlier results to build toward complex parts
- If stuck, move on and return later
- Show all steps clearly for partial credit
Conclusion and Future Connections
Electromagnetic wave theory represents one of the most successful unifications in physics history. Maxwell’s elegant mathematical framework not only explained known electrical and magnetic phenomena but predicted entirely new physics – the existence of electromagnetic waves and their identification with light. This theoretical triumph exemplifies how mathematical beauty often guides us toward profound physical truths.
Your mastery of electromagnetic waves provides the foundation for understanding numerous advanced topics in physics and engineering. In quantum mechanics, you’ll discover that electromagnetic waves also behave as particles (photons), leading to wave-particle duality. Special relativity emerges from the universal speed limit imposed by electromagnetic waves. Modern physics courses will build on these concepts to explain atomic structure, solid-state physics, and quantum field theory.
The practical importance of electromagnetic wave theory continues expanding with technological advancement. 5G communication networks, quantum computing, medical imaging improvements, and space exploration all rely fundamentally on principles you’ve studied in this chapter. Understanding electromagnetic waves isn’t just academic knowledge – it’s the key to comprehending and developing the technologies that will shape our future.
Real-World Physics: As you’ve learned electromagnetic wave theory, you’ve actually been experiencing it constantly. The light reaching your eyes, the radio waves connecting your devices, the infrared radiation warming your skin, and the X-rays used in medical checkups all follow the same fundamental principles Maxwell discovered over 150 years ago. This universality is one of physics’ most beautiful aspects – the same equations that describe radio transmission also govern starlight crossing interstellar space.
Study Recommendations for Continued Success
Connect to Other Physics Topics: Look for electromagnetic wave concepts in optics, atomic physics, and modern physics chapters. The unified perspective strengthens understanding across all areas.
Practice Real Calculations: Work with actual values from technology specifications. Calculate cell phone frequencies, satellite communication delays, or solar panel efficiencies using electromagnetic wave theory.
Explore Current Research: Follow developments in electromagnetic metamaterials, terahertz technology, and optical computing. These cutting-edge fields directly apply the principles you’ve learned.
Laboratory Experience: Seek opportunities to work with electromagnetic waves experimentally. Many physics concepts become clearer through hands-on investigation.
Remember that physics is ultimately about understanding the natural world around us. Electromagnetic wave theory provides a powerful lens for seeing the invisible forces and fields that surround us constantly. As you continue your physics journey, carry forward the appreciation for both the mathematical elegance and practical power of Maxwell’s electromagnetic theory.
Your success in mastering this chapter demonstrates your ability to handle sophisticated physics concepts. These same analytical and problem-solving skills will serve you well in advanced physics courses, engineering applications, and scientific research. The universe operates according to physical laws, and electromagnetic theory gives you insight into some of the most fundamental and beautiful of these principles.
Final Physics Check: Before your exam, verify that you can explain electromagnetic waves to someone unfamiliar with physics, solve representative problems confidently, and connect the theory to real-world applications. This comprehensive understanding will ensure success not just on exams, but in appreciating the electromagnetic phenomena that surround us every day.
This comprehensive study guide provides the theoretical foundation, practical applications, problem-solving strategies, and exam preparation techniques needed to excel in CBSE Class 12 Physics Chapter 8 on Electromagnetic Waves. The guide balances mathematical rigor with conceptual understanding while maintaining the engaging, conversational tone that helps students connect with complex physics concepts.
Recommended –


2 thoughts on “CBSE Class 12 Physics Chapter 8 – Electromagnetic Waves: Complete Study Guide for Board Exam Success”