Picture this: You’re watching a figure skater perform a breathtaking spin, pulling their arms close to their body and suddenly rotating faster than your eyes can follow. Or maybe you’ve marveled at how a bicycle wheel keeps a bike stable, or wondered why a spinning top defies gravity for so long. These mesmerizing phenomena aren’t just beautiful to watch-they’re perfect examples of the fascinating physics principles you’ll master in AP Physics 1 Unit 6 – Energy and Momentum of Rotating Systems.
Welcome to the world of rotational motion, where spinning objects follow surprisingly elegant mathematical relationships that mirror the linear motion you’ve already studied. This unit builds beautifully on everything you’ve learned about forces, energy, and momentum, extending these concepts into the realm of rotation. By the end of this comprehensive guide, you’ll not only understand why that figure skater spins faster when pulling in their arms, but you’ll also be able to solve complex problems involving rotating systems with confidence.
Learning Objectives: What You’ll Master in This Unit
According to the College Board AP Physics 1 Course and Exam Description, this unit focuses on several key learning objectives that will transform how you think about rotating objects:
Essential Knowledge 4.D.1: You’ll learn to calculate the rotational kinetic energy of rotating systems and understand how it relates to both rotational inertia and angular velocity.
Essential Knowledge 4.D.2: You’ll master the principle of conservation of angular momentum and apply it to analyze collisions and interactions involving rotating objects.
Essential Knowledge 4.D.3: You’ll understand how torque relates to changes in angular momentum, just as force relates to changes in linear momentum.
These objectives aren’t just academic checkboxes-they’re the foundation for understanding everything from the gyroscopes in your smartphone to the turbines that generate electricity. Let’s dive into this rotational world and discover the elegant physics that governs spinning systems.
Understanding Rotational Kinetic Energy: When Spinning Objects Store Energy
The Foundation: Kinetic Energy Takes a New Form
You already know that moving objects possess kinetic energy given by KE = ½mv². But what happens when an object spins rather than moves in a straight line? This is where rotational kinetic energy comes into play, and it’s one of the most beautiful extensions of familiar physics principles.
When a wheel spins, a DVD rotates, or a planet turns on its axis, each part of the object is moving in a circle. The faster the object spins and the more mass it has distributed away from its rotation axis, the more rotational kinetic energy it possesses. This energy is captured by the elegant equation:
KE_rotational = ½Iω²
Where I represents the rotational inertia (also called moment of inertia) and ω (omega) represents the angular velocity. Notice how this mirrors the linear kinetic energy formula-it’s the same mathematical structure with rotational quantities replacing their linear counterparts.
Rotational Inertia: The Resistance to Rotational Motion
Rotational inertia (I) is perhaps the most conceptually challenging part of rotational motion, but understanding it is crucial for AP Physics 1 success. Think of rotational inertia as the rotational equivalent of mass-it measures how difficult it is to change an object’s rotational motion.
However, unlike mass, rotational inertia depends not just on how much mass an object has, but also on how that mass is distributed relative to the rotation axis. A figure skater demonstrates this beautifully: when their arms are extended, their rotational inertia is large, making them harder to spin. When they pull their arms close to their body, their rotational inertia decreases dramatically.
For the AP Physics 1 exam, you’ll primarily work with three standard shapes:
Point mass at distance r from axis: I = mr²
Solid disk or cylinder: I = ½MR²
Solid sphere: I = ⅖MR²
Physics Check: Why does rotational inertia increase with the square of the distance? Consider a small mass m located at distance r from the rotation axis. As it rotates, its linear speed is v = rω. Its kinetic energy is ½mv² = ½m(rω)² = ½mr²ω². For the total rotational kinetic energy to equal ½Iω², we need I = mr² for a point mass.
Angular Velocity: Describing How Fast Things Spin
Angular velocity (ω) measures how quickly an object rotates, typically expressed in radians per second. One complete rotation equals 2π radians, so an object making one revolution per second has an angular velocity of 2π rad/s.
The relationship between linear and angular quantities provides powerful problem-solving tools:
- Linear velocity: v = rω
- Linear acceleration: a = rα (where α is angular acceleration)
- Arc length: s = rθ (where θ is the angle in radians)
Real-World Physics: Your car’s speedometer actually measures the rotational speed of your wheels and converts it to linear speed using v = rω. A typical car tire has a radius of about 0.3 meters, so when you’re driving at 60 mph (27 m/s), your wheels are rotating at ω = v/r = 27/0.3 = 90 rad/s, or about 14 revolutions per second!
Conservation of Angular Momentum: The Spinning Universe’s Most Fundamental Law
Defining Angular Momentum
Angular momentum (L) is the rotational equivalent of linear momentum, and its conservation is one of the most powerful principles in physics. For a rotating rigid body, angular momentum is defined as:
L = Iω
Just as linear momentum equals mass times velocity (p = mv), angular momentum equals rotational inertia times angular velocity. This seemingly simple relationship has profound implications for everything from atomic structure to galactic rotation.

The Conservation Principle in Action
The conservation of angular momentum states that in the absence of external torques, the total angular momentum of a system remains constant. This principle explains countless phenomena you observe daily:
The Figure Skater Effect: When a skater pulls their arms inward, their rotational inertia decreases. Since angular momentum must be conserved (L = Iω = constant), their angular velocity must increase to compensate. The math is beautiful: if the skater reduces their rotational inertia by half, their spinning speed doubles.
The Bicycle Wheel Gyroscope: When you try to tilt a rapidly spinning bicycle wheel, it resists the change in orientation. The wheel’s angular momentum vector wants to maintain its direction, creating the mysterious gyroscopic effect that helps keep bicycles stable.
Planetary Motion: Earth’s angular momentum about the Sun remains essentially constant, which is why our orbital speed increases when we’re closer to the Sun (during winter in the Northern Hemisphere) and decreases when we’re farther away.
Problem-Solving Strategy: Angular Momentum Conservation
When approaching angular momentum problems, follow this systematic approach:
- Identify the system: Clearly define what objects are included and whether external torques act on the system.
- Check for conservation: If no external torques act, angular momentum is conserved: L_initial = L_final.
- Write conservation equations: Set up I₁ω₁ = I₂ω₂ for each object or system component.
- Solve systematically: Use algebra to find unknown quantities, being careful with units and significant figures.
Sample Problem: A figure skater is spinning with arms extended at 2.0 rev/s. Her rotational inertia in this position is 5.0 kg⋅m². When she pulls her arms to her sides, her rotational inertia becomes 1.8 kg⋅m². What is her new angular velocity?
Solution:
Using conservation of angular momentum: L₁ = L₂
I₁ω₁ = I₂ω₂
(5.0 kg⋅m²)(2.0 rev/s) = (1.8 kg⋅m²)ω₂
ω₂ = (5.0 × 2.0)/1.8 = 5.6 rev/s
The skater spins nearly three times faster!
Torque and Angular Momentum: The Rotational Force-Momentum Connection
Understanding Torque as the Agent of Change
Just as force causes changes in linear momentum (F = dp/dt), torque causes changes in angular momentum. This relationship, known as the rotational form of Newton’s second law, is expressed as:
τ = dL/dt
For a rigid body with constant rotational inertia, this simplifies to the familiar form τ = Iα, where α is angular acceleration. However, the more general form τ = dL/dt is crucial for understanding systems where rotational inertia changes, such as our spinning figure skater.
Calculating Torque: The Rotational Force
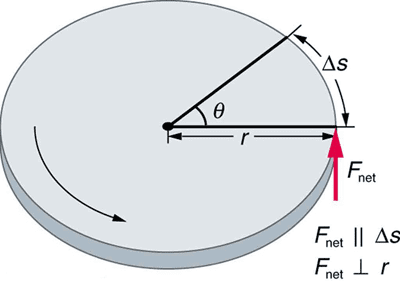
Torque measures the tendency of a force to cause rotation about an axis. The magnitude of torque depends on three factors:
- The magnitude of the applied force (F)
- The distance from the rotation axis to where the force is applied (r)
- The angle between the force vector and the position vector (θ)
The torque magnitude is given by: τ = rF sin θ
The direction of torque follows the right-hand rule: point your fingers in the direction of the position vector, curl them toward the force vector, and your thumb points in the direction of the torque vector.

Physics Check: Why is it easier to open a door by pushing near the handle rather than near the hinges? The torque equation τ = rF sin θ shows that torque increases with distance from the rotation axis. When you push at the door handle, r is maximum, giving you the greatest mechanical advantage.
Applications in Problem-Solving
Understanding the torque-angular momentum relationship is essential for solving complex rotational problems, especially those involving changing rotational inertia or multiple interacting objects.
Common Mistake Alert: Students often confuse the direction of angular velocity and angular momentum vectors. Remember, these vectors point along the rotation axis according to the right-hand rule, not in the direction of motion of the rotating object.
Energy in Rotating Systems: When Translation Meets Rotation
Total Kinetic Energy: The Complete Picture
Many real-world objects don’t just rotate-they roll. A rolling wheel, a rolling sphere, or a bicycle tire combines both translational and rotational motion. The total kinetic energy of such objects is the sum of their translational and rotational kinetic energies:
KE_total = KE_translational + KE_rotational = ½mv² + ½Iω²
For an object rolling without slipping, there’s a crucial constraint: v = rω. This relationship connects the linear and angular velocities and is key to solving rolling problems.
Rolling Without Slipping: A Special Condition
When an object rolls without slipping, the point of contact between the object and the surface has zero velocity relative to the surface. This constraint leads to the condition v = rω and has important energy implications.
Sample Problem: A solid sphere of mass 2.0 kg and radius 0.15 m rolls down a hill with a linear speed of 3.0 m/s at the bottom. Calculate its total kinetic energy.
Solution:
For a solid sphere, I = ⅖MR² = ⅖(2.0)(0.15)² = 0.018 kg⋅m²
Since v = rω, we have ω = v/r = 3.0/0.15 = 20 rad/s
KE_translational = ½mv² = ½(2.0)(3.0)² = 9.0 J
KE_rotational = ½Iω² = ½(0.018)(20)² = 3.6 J
KE_total = 9.0 + 3.6 = 12.6 J
Notice that for a rolling sphere, the rotational kinetic energy is 2/5 of the translational kinetic energy!

Conservation of Energy in Rotational Systems
Energy conservation in rotational systems follows the same principles as in translational systems, but now you must account for rotational kinetic energy. The total mechanical energy includes:
E_total = KE_translational + KE_rotational + PE = ½mv² + ½Iω² + mgh
This expanded energy equation is particularly powerful for analyzing objects rolling down inclines or swinging on strings.
Rotational Dynamics: Newton’s Laws in a Spinning World
Newton’s Second Law for Rotation
The rotational analog of F = ma is τ = Iα, where τ is the net torque, I is the rotational inertia, and α is the angular acceleration. This relationship allows you to analyze the motion of rotating objects when torques are applied.
For objects with changing rotational inertia (like our figure skater), the more general form τ = dL/dt is necessary. This leads to fascinating phenomena where objects can change their rotation rate even when no external torque is applied, simply by changing their shape.
Equilibrium in Rotational Systems
For an object to be in rotational equilibrium, the net torque about any axis must be zero: Στ = 0. This condition, combined with translational equilibrium (ΣF = 0), allows you to analyze complex static systems like levers, seesaws, and architectural structures.
Problem-Solving Strategy: When solving equilibrium problems:
- Choose a convenient axis of rotation (often where an unknown force acts)
- Calculate torques about this axis, being careful with signs
- Set the sum of torques equal to zero
- Solve for unknown quantities
Applications to Real-World Systems
Understanding rotational dynamics helps explain countless everyday phenomena:
Gyroscopic Stability: Spinning tops, gyroscopes, and bicycle wheels resist changes to their orientation due to conservation of angular momentum. This principle is used in navigation systems, stabilizing platforms, and even in the attitude control of spacecraft.
Engine Balancing: Car engines use counterbalancing masses to minimize vibrations from rotating and reciprocating parts. The principles of rotational inertia and angular momentum are crucial for smooth engine operation.
Angular Impulse and Angular Momentum: The Rotational Impulse-Momentum Theorem
The Rotational Impulse-Momentum Theorem
Just as linear impulse equals the change in linear momentum (J = Δp), angular impulse equals the change in angular momentum. The angular impulse-momentum theorem states:
Angular Impulse = ∫τ dt = ΔL = L_final – L_initial
For constant torque, this simplifies to: τΔt = ΔL
This relationship is particularly useful for analyzing brief interactions, such as when a torque is applied to a rotating object for a short time period.
Applications in Problem-Solving
The angular impulse-momentum theorem is especially powerful for analyzing situations where:
- A torque acts for a known time interval
- You need to find the final angular velocity after an impulse
- You’re analyzing collisions involving rotating objects
Sample Problem: A potter’s wheel (I = 0.50 kg⋅m²) is spinning at 60 rpm when the potter applies a constant torque of 0.20 N⋅m for 3.0 seconds to slow it down. What is the wheel’s final angular velocity?
Solution:
First, convert initial angular velocity: ω₁ = 60 rpm = 60 × (2π/60) = 6.3 rad/s
Initial angular momentum: L₁ = Iω₁ = (0.50)(6.3) = 3.15 kg⋅m²/s
The torque opposes rotation, so it’s negative: τ = -0.20 N⋅m
Angular impulse: τΔt = (-0.20)(3.0) = -0.60 N⋅m⋅s
Using the impulse-momentum theorem:
ΔL = τΔt = -0.60 kg⋅m²/s
L₂ = L₁ + ΔL = 3.15 – 0.60 = 2.55 kg⋅m²/s
ω₂ = L₂/I = 2.55/0.50 = 5.1 rad/s = 49 rpm
Collisions in Rotational Systems: When Spinning Objects Interact
Elastic and Inelastic Rotational Collisions
When rotating objects collide or interact, both angular momentum and energy considerations come into play. Just as in linear collisions, rotational collisions can be elastic (kinetic energy conserved) or inelastic (kinetic energy not conserved, but angular momentum still conserved in the absence of external torques).
The Classic Rotating Platform Problem
One of the most common AP Physics 1 scenarios involves a person jumping onto or off a rotating platform. These problems beautifully demonstrate conservation of angular momentum and the relationship between rotational inertia and angular velocity.
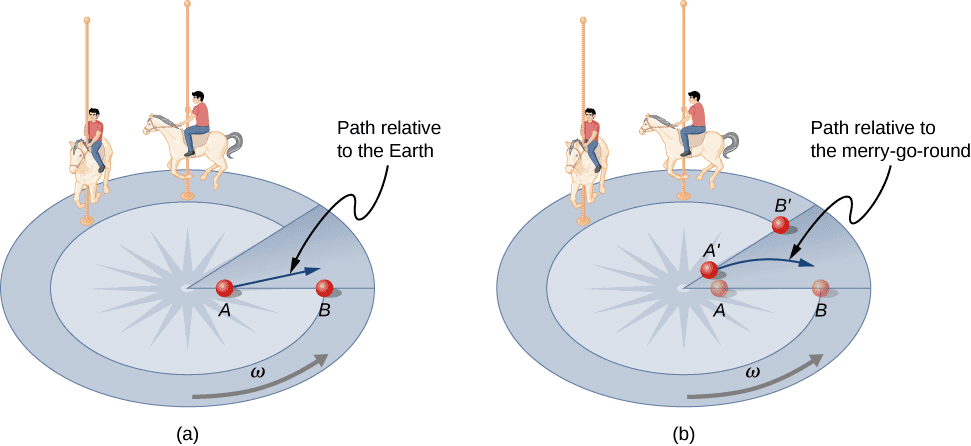
Sample Problem: A 60-kg student stands at the edge of a 2.0-m radius merry-go-round (I = 500 kg⋅m²) that’s rotating at 0.50 rad/s. The student walks to the center. What is the new angular velocity of the system?
Solution:
Initially, the student is at radius r = 2.0 m, so I_student = mr² = (60)(2.0)² = 240 kg⋅m²
I_initial = I_merry-go-round + I_student = 500 + 240 = 740 kg⋅m²
L_initial = I_initial × ω_initial = (740)(0.50) = 370 kg⋅m²/s
Finally, the student is at the center (r = 0), so I_student = 0
I_final = 500 kg⋅m²
Using conservation of angular momentum:
L_final = L_initial
(500)ω_final = 370
ω_final = 370/500 = 0.74 rad/s
The system speeds up as the student moves toward the center!
Energy Considerations in Rotational Collisions
When analyzing rotational collisions, it’s important to check whether kinetic energy is conserved. In many real-world situations, some rotational kinetic energy is converted to other forms (heat, sound, deformation), making the collision inelastic.
Real-World Physics: When a spinning figure skater catches a thrown object, the collision is typically inelastic. Angular momentum is conserved, but some kinetic energy is lost to heat and deformation. However, the skater can still use the principle to analyze the resulting motion.
Advanced Applications: Gyroscopes and Precession
Understanding Gyroscopic Motion
Gyroscopes exhibit one of the most counterintuitive behaviors in physics: when you try to tilt a spinning gyroscope, it doesn’t fall as expected but instead precesses-rotating about a different axis. This behavior results from the vector nature of angular momentum and the relationship τ = dL/dt.
When a torque is applied to a spinning gyroscope, it doesn’t change the magnitude of the angular momentum but rather changes its direction. This creates the fascinating precession motion observed in spinning tops, bicycle wheels, and navigation gyroscopes.
The Physics of Precession
The precession angular velocity ωₚ is given by:
ωₚ = τ/L = τ/(Iω)
Where τ is the applied torque, L is the angular momentum, I is the rotational inertia, and ω is the spin angular velocity. Notice that faster-spinning gyroscopes precess more slowly-this is why a rapidly spinning top is more stable.
Physics Check: Why doesn’t a spinning bicycle wheel fall when you hold it by one end? The wheel’s angular momentum vector points along its axis. Gravity creates a torque that tries to change this angular momentum vector’s direction, not its magnitude. Instead of falling, the wheel precesses, maintaining its angular momentum magnitude while slowly rotating the direction of its angular momentum vector.
Experimental Investigations: Measuring Rotational Quantities
Investigating Rotational Inertia
A common AP Physics 1 investigation involves measuring how rotational inertia affects the motion of objects rolling down inclines. By comparing spheres, cylinders, and rings of different masses and sizes, you can verify theoretical predictions about rotational inertia.
Experimental Design: Set up an incline and time objects as they roll down. Using energy conservation (mgh = ½mv² + ½Iω²) and the rolling condition (v = rω), you can derive that the acceleration down the incline depends only on the shape of the object, not its mass or size:
For a solid sphere: a = (5/7)g sin θ
For a solid cylinder: a = (2/3)g sin θ
For a ring: a = (1/2)g sin θ
This remarkable result means that in a rolling race, shape matters more than size or mass!
Measuring Angular Momentum Conservation
Another powerful investigation involves measuring angular momentum before and after interactions. Using rotating platforms, spinning wheels, or even simple tops, you can verify that angular momentum is conserved in isolated systems.
Data Analysis Techniques: When analyzing rotational motion data, pay careful attention to:
- Converting between different angular units (degrees, radians, revolutions)
- Measuring angular velocity accurately using video analysis or photogate timers
- Calculating uncertainties in derived quantities like rotational kinetic energy
- Identifying sources of error, such as friction and air resistance

Problem-Solving Strategies: Mastering Rotational Motion
The Systematic Approach
Successful problem-solving in rotational motion requires a systematic approach that parallels what you’ve learned for linear motion:
- Identify the type of motion: Pure rotation, pure translation, or combined (rolling)
- Draw clear diagrams: Include rotation axes, force vectors, and relevant distances
- Choose appropriate principles: Conservation laws, Newton’s laws, or energy methods
- Set up equations carefully: Pay attention to signs and vector directions
- Check your answer: Verify units, magnitudes, and physical reasonableness
Common Problem Types
Type 1: Conservation of Angular Momentum
- Identify isolated system with no external torques
- Apply L_initial = L_final
- Often involves changing rotational inertia
Type 2: Torque and Angular Acceleration
- Identify all torques acting on the object
- Apply τ_net = Iα
- May require combining with linear motion equations
Type 3: Energy Methods
- Include both translational and rotational kinetic energy
- Apply conservation of energy or work-energy theorem
- Particularly useful for rolling objects on inclines
Type 4: Combined Motion
- Objects that both translate and rotate
- Use constraints like v = rω for rolling without slipping
- Often requires multiple conservation laws simultaneously
Avoiding Common Mistakes
Mistake 1: Forgetting the rolling condition v = rω
Solution: Always check whether objects are rolling, sliding, or purely rotating
Mistake 2: Using wrong rotational inertia formulas
Solution: Memorize the standard formulas and understand when each applies
Mistake 3: Sign errors in torque calculations
Solution: Establish a clear sign convention and stick to it throughout the problem
Mistake 4: Mixing up angular momentum and angular velocity
Solution: Remember L = Iω; angular momentum depends on both rotational inertia and angular velocity
Connections to Other AP Physics 1 Units
Building on Previous Knowledge
Rotational motion beautifully extends concepts from earlier units:
From Unit 1 (Kinematics): Linear kinematic equations have rotational analogs
- s = vt becomes θ = ωt
- v = v₀ + at becomes ω = ω₀ + αt
- s = v₀t + ½at² becomes θ = ω₀t + ½αt²
From Unit 2 (Dynamics): Newton’s laws extend to rotation
- F = ma becomes τ = Iα
- Net force causes acceleration becomes net torque causes angular acceleration
From Unit 3 (Circular Motion): Provides the foundation for rotational motion
- Centripetal acceleration connects linear and angular quantities
- Circular motion concepts help understand rotation
From Unit 4 (Energy): Energy conservation includes rotational kinetic energy
- Total energy now includes KE_rotational = ½Iω²
- Work-energy theorem extends to rotational work
From Unit 5 (Momentum): Momentum conservation has a rotational analog
- p = mv becomes L = Iω
- Impulse-momentum theorem becomes angular impulse-angular momentum theorem
Looking Ahead
The concepts in this unit prepare you for advanced physics topics:
- Quantum mechanics: Angular momentum is quantized in atomic systems
- Electromagnetism: Rotating charges create magnetic fields
- Thermodynamics: Rotational energy contributes to molecular heat capacity
- Astrophysics: Angular momentum conservation governs stellar evolution
Real-World Applications: Rotational Physics in Technology and Nature
Engineering Applications
Modern technology heavily relies on rotational motion principles:
Wind Turbines: Engineers optimize blade design using rotational inertia principles to maximize energy extraction from wind. The variable pitch blades can change their rotational inertia to maintain optimal rotation rates in varying wind conditions.
Hard Drives and SSDs: Traditional hard drives store data on rotating disks, with read/write heads that must account for the disk’s angular momentum. Even solid-state drives use principles of rotational motion in their design algorithms.
Gyroscopic Sensors: Your smartphone uses tiny gyroscopes to detect orientation changes. These devices rely on the conservation of angular momentum to measure rotation rates with incredible precision.
Sports and Recreation
Many sports demonstrate rotational motion principles:
Figure Skating: Skaters manipulate their rotational inertia to control spin rates, demonstrating conservation of angular momentum in real-time.
Diving and Gymnastics: Athletes adjust their body positions to control rotation rates during flips and twists, using the same physics principles.
Bicycle Stability: The gyroscopic effect of spinning wheels contributes to bicycle stability, though it’s not the only factor.
Golf and Tennis: Ball spin affects trajectory and bounce characteristics, involving both rotational and translational motion.
Natural Phenomena
Nature provides countless examples of rotational motion:
Planetary Motion: Earth’s rotation rate slowly decreases due to tidal friction, but angular momentum is conserved by the Moon moving gradually farther away.
Hurricanes and Tornadoes: These weather systems demonstrate conservation of angular momentum as air masses spiral inward and speed up.
Galaxy Rotation: Spiral galaxies rotate as rigid bodies in their centers but follow different rotation curves in their outer regions, leading to discoveries about dark matter.
Advanced Problem-Solving: Multi-Step Rotational Problems
Complex System Analysis
Advanced AP Physics 1 problems often involve multiple objects, changing conditions, or combined motions. These problems require careful analysis and systematic application of multiple physics principles.
Sample Complex Problem: A 2.0-kg solid cylinder (radius 0.15 m) rolls without slipping down a 30° incline that’s 2.0 m long. At the bottom, it encounters a horizontal surface with friction coefficient μ = 0.20. How far does it slide before coming to rest?
Solution Strategy:
- Phase 1: Rolling down incline – use energy conservation
- Phase 2: Sliding on horizontal surface – use work-energy theorem
Phase 1 Analysis:
Initial energy: E₁ = mgh = (2.0)(9.8)(2.0 sin 30°) = 19.6 J
Final energy: E₂ = ½mv² + ½Iω²
For rolling without slipping: v = rω and I = ½mr²
E₂ = ½mv² + ½(½mr²)(v/r)² = ½mv² + ¼mv² = ¾mv²
Energy conservation: 19.6 = ¾mv²
v² = 19.6/(¾ × 2.0) = 13.1 m²/s²
v = 3.6 m/s
Phase 2 Analysis:
Initial kinetic energy: KE = ½mv² = ½(2.0)(13.1) = 13.1 J
Work done by friction: W = -μmgd = -0.20(2.0)(9.8)d = -3.92d
Using work-energy theorem: -3.92d = 0 – 13.1
d = 13.1/3.92 = 3.3 m
Problem-Solving Toolkit: Essential Strategies
Strategy 1: Energy Methods
- Most powerful for problems involving motion along paths
- Include all forms of kinetic and potential energy
- Particularly useful for rolling objects on inclines
Strategy 2: Conservation Laws
- Angular momentum conservation for isolated systems
- Energy conservation when only conservative forces act
- Often provides elegant solutions to complex problems
Strategy 3: Force and Torque Analysis
- Essential when accelerations are involved
- Use free-body diagrams and torque diagrams
- Apply Newton’s laws in both linear and rotational forms
Strategy 4: Constraint Equations
- Rolling without slipping: v = rω
- Strings and pulleys: relate linear and angular motions
- These equations often provide crucial relationships
Exam Preparation: Mastering AP Physics 1 Unit 6
High-Yield Topics for the AP Exam
Based on College Board data and past exam trends, focus your review on these frequently tested concepts:
- Conservation of Angular Momentum (Very High Yield)
- Figure skater problems
- Rotating platform scenarios
- Collision problems involving rotation
- Rolling Motion (High Yield)
- Objects rolling down inclines
- Relationship between v and ω
- Energy analysis of rolling objects
- Rotational Kinetic Energy (High Yield)
- Calculating KE_rotational = ½Iω²
- Comparing different shapes
- Total energy in rolling systems
- Torque and Angular Acceleration (Medium-High Yield)
- τ = rF sin θ calculations
- τ = Iα applications
- Equilibrium problems
Free Response Question Strategies
AP Physics 1 free response questions in this unit typically fall into these categories:
Experimental Design Questions:
- Design experiments to measure rotational inertia
- Investigate factors affecting rolling motion
- Analyze data from rotational motion experiments
Qualitative/Quantitative Translation:
- Explain physical phenomena using rotational concepts
- Predict motion based on conservation laws
- Justify answers using physics principles
Problem-Solving with Multiple Parts:
- Multi-step problems involving energy and momentum
- Combined linear and rotational motion
- Real-world applications of rotational principles
Time Management Tips
For multiple choice questions:
- Quickly identify the physical principle involved
- Use dimensional analysis to eliminate wrong answers
- Look for conservation law applications
For free response questions:
- Spend time planning your approach before writing
- Show all work clearly, including equation setup
- Check your answer for reasonableness
- Use proper physics vocabulary and notation
Practice Problems: Testing Your Understanding
Multiple Choice Practice
Problem 1: A solid sphere and a solid cylinder of equal mass and radius roll down identical inclines. Which reaches the bottom first?
A) The sphere
B) The cylinder
C) They reach the bottom simultaneously
D) It depends on their masses
Answer: A – The sphere reaches the bottom first because it has smaller rotational inertia (I = ⅖mr² vs ½mr²), allowing more of its potential energy to become translational kinetic energy.
Problem 2: A figure skater spinning at 3.0 rev/s extends her arms, doubling her rotational inertia. Her new angular velocity is:
A) 1.5 rev/s
B) 3.0 rev/s
C) 6.0 rev/s
D) 12 rev/s
Answer: A – Angular momentum is conserved: I₁ω₁ = I₂ω₂. If I₂ = 2I₁, then ω₂ = ω₁/2 = 1.5 rev/s.
Free Response Practice
Problem 3: A student conducts an experiment rolling different objects down an incline. She measures the time for each object to travel 2.0 m down a 20° incline and obtains these results:
- Solid sphere: 1.8 s
- Solid cylinder: 2.0 s
- Ring: 2.5 s
a) Derive the theoretical acceleration for each shape rolling down the incline.
b) Calculate the predicted times and compare with experimental results.
c) Identify sources of experimental error and suggest improvements.
Solution approach:
a) Use energy conservation: mgh = ½mv² + ½Iω² with v = rω
This gives: a = g sin θ/(1 + I/mr²)
Sphere: a = g sin θ/(1 + 2/5) = (5/7)g sin θ
Cylinder: a = g sin θ/(1 + 1/2) = (2/3)g sin θ
Ring: a = g sin θ/(1 + 1) = (1/2)g sin θ
b) Using s = ½at², solve for t = √(2s/a) for each shape
c) Error sources: air resistance, rolling friction, measurement precision
Key Physics Concepts Summary
As we conclude this comprehensive exploration of AP Physics 1 Unit 6, let’s consolidate the essential concepts you’ve mastered:
Rotational Kinetic Energy: KE_rot = ½Iω² extends the familiar kinetic energy concept to rotating objects, where rotational inertia I plays the role of mass and angular velocity ω plays the role of linear velocity.
Conservation of Angular Momentum: In the absence of external torques, L = Iω remains constant, explaining phenomena from figure skaters to planetary motion.
Torque and Angular Motion: τ = Iα connects rotational force (torque) to rotational acceleration, while τ = dL/dt relates torque to changes in angular momentum.
Rolling Motion: Objects that roll without slipping follow the constraint v = rω, and their total kinetic energy includes both translational and rotational components.
Energy Conservation: Total mechanical energy in rotational systems includes gravitational potential energy, translational kinetic energy, and rotational kinetic energy.
These concepts aren’t just academic abstractions-they’re the fundamental principles governing countless technologies and natural phenomena that surround you daily.
Formula Sheet and Quick Reference
Essential Equations
Rotational Kinematics:
- θ = ω₀t + ½αt²
- ω = ω₀ + αt
- ω² = ω₀² + 2αθ
Rotational Dynamics:
- τ = Iα
- τ = rF sin θ
- L = Iω
Energy and Rolling:
- KE_rot = ½Iω²
- v = rω (rolling without slipping)
- KE_total = ½mv² + ½Iω²
Standard Rotational Inertias:
- Point mass: I = mr²
- Solid disk/cylinder: I = ½mr²
- Solid sphere: I = ⅖mr²
- Ring/hollow cylinder: I = mr²
Conservation Laws
- Angular momentum: L₁ = L₂ (no external torques)
- Energy: E₁ = E₂ (conservative forces only)
- Angular impulse: τΔt = ΔL
This comprehensive guide has equipped you with everything you need to excel in AP Physics 1 Unit 6. The world of rotational motion, from spinning figure skaters to orbiting planets, now makes physical sense through the elegant mathematical relationships you’ve mastered. Remember, success in physics comes not just from memorizing formulas, but from understanding the underlying principles and developing problem-solving strategies that work across different contexts.
As you continue your physics journey, you’ll find that the concepts in this unit provide a crucial foundation for advanced topics in engineering, astronomy, and quantum mechanics. The angular momentum you’ve studied here governs the behavior of atoms, the formation of galaxies, and the operation of countless technologies that shape our modern world.
Keep practicing, stay curious, and remember that every spinning object around you is demonstrating the beautiful physics principles you’ve now mastered. Good luck on your AP Physics 1 exam!
Recommended –


3 thoughts on “AP Physics 1 Unit 6: Energy and Momentum of Rotating Systems – Complete Guide”