Have you ever wondered why a massive steel ship floats effortlessly on water while a small pebble sinks instantly? Or how a straw works to draw liquid up into your mouth, seemingly defying gravity? These everyday phenomena showcase the fascinating world of fluid mechanics – one of physics’ most practically relevant topics that surrounds us in everything from the blood flowing through our veins to the aerodynamics of airplanes soaring overhead.
Welcome to Unit 8 of AP Physics 1, where we’ll dive deep into the behavior of fluids and discover the fundamental principles that govern how liquids and gases interact with objects and move through space. This comprehensive guide will transform your understanding of fluid mechanics from mysterious observations into clear, predictable physics concepts that you can confidently apply on exam day and beyond.
Learning Objectives: What You’ll Master
By the end of this unit, you’ll have developed a robust understanding of fluid mechanics that extends far beyond memorizing formulas. You’ll be able to:
- Analyze pressure variations in static fluids and predict how pressure changes with depth and density
- Apply Archimedes’ principle to determine buoyant forces and predict whether objects will float or sink
- Understand fluid flow dynamics including the relationship between flow rate, cross-sectional area, and fluid velocity
- Solve complex problems involving floating objects, submerged bodies, and fluid motion using both mathematical and conceptual approaches
- Design and analyze experiments that investigate fluid properties and behaviors
- Connect fluid mechanics to real-world applications in engineering, biology, and environmental science
These skills align directly with the College Board’s emphasis on scientific practices and cross-cutting concepts, preparing you not just for the AP exam but for future coursework in physics, engineering, and related fields.
The Foundation: Understanding What Makes a Fluid
Before we explore the complex behaviors of fluids, let’s establish what we mean by “fluid” in physics. A fluid is any substance that can flow and take the shape of its container – this includes both liquids like water and mercury, and gases like air and helium. What distinguishes fluids from solids is their inability to maintain a fixed shape when subjected to even small forces.
Think about pouring honey versus moving a block of wood. The honey, despite being viscous, will eventually flow and conform to whatever container you place it in. The wood, however, maintains its shape regardless of the container. This fundamental difference in molecular behavior creates all the interesting phenomena we’ll study in this unit.
Real-World Physics: The distinction between fluids and solids isn’t always clear-cut. Materials like silly putty or certain plastics can behave as solids under quick forces but flow like fluids under sustained pressure. This property, called viscoelasticity, is crucial in designing everything from car bumpers to earthquake-resistant buildings.
Pressure: The Hidden Force in Fluids
Understanding Pressure Fundamentals
Pressure represents one of the most important concepts in fluid mechanics, yet it’s often misunderstood by students. Pressure is defined as the force per unit area exerted by a fluid on any surface in contact with it:
P = F/A
Where P is pressure (measured in Pascals, Pa), F is the perpendicular force (in Newtons), and A is the area over which the force is distributed (in square meters).
The key insight here is that fluids exert pressure equally in all directions at any given point. This might seem counterintuitive – after all, we think of pressure as something that pushes “down” due to gravity. However, the molecular motion of fluid particles creates forces in every direction, not just downward.
Physics Check: A common misconception is that pressure only acts downward in fluids. In reality, fluid pressure at any point acts equally in all directions – up, down, left, right, and diagonally. This is why a balloon expands uniformly in all directions when inflated, and why fish don’t get crushed by the “weight” of water above them (though they do experience uniform pressure from all sides).
Pressure Variation with Depth
One of the most practically important relationships in fluid mechanics describes how pressure changes with depth in a static fluid. For an incompressible fluid in a gravitational field, pressure increases linearly with depth according to:
P = P₀ + ρgh
Where:
- P is the pressure at depth h
- P₀ is the pressure at the surface (often atmospheric pressure)
- ρ (rho) is the fluid density
- g is gravitational acceleration
- h is the depth below the surface
This equation tells us several important things. First, pressure increases linearly with depth – double the depth, double the additional pressure. Second, denser fluids create greater pressure increases with depth. Third, the pressure at any given depth depends only on the vertical distance below the surface, not on the shape of the container or the total volume of fluid.
Real-World Physics: This pressure-depth relationship explains why deep-sea creatures have specialized adaptations to survive extreme pressures, why submarines must be incredibly strong, and why your ears “pop” when diving to the bottom of a deep pool. At the deepest part of the ocean (about 11,000 meters), the pressure is over 1,000 times greater than at sea level!
Atmospheric Pressure and Gauge Pressure
Understanding atmospheric pressure is crucial for solving fluid problems correctly. At sea level, atmospheric pressure equals approximately 101,325 Pa (or 1 atmosphere). This pressure exists because we live at the bottom of an “ocean” of air extending dozens of kilometers above us.
In many practical situations, we measure gauge pressure – the pressure relative to atmospheric pressure rather than absolute pressure. For example, when you check your tire pressure and it reads 32 psi, that’s gauge pressure. The absolute pressure inside the tire is actually 32 psi plus atmospheric pressure (about 14.7 psi at sea level).
Problem-Solving Strategy: Always clarify whether a problem is asking for gauge pressure or absolute pressure. For problems involving open containers or objects at the surface of fluids, you’ll often need to add atmospheric pressure to your calculated pressure difference.
Pascal’s Principle: Pressure Transmission in Fluids
Pascal’s principle, discovered by French mathematician Blaise Pascal, states that pressure applied to a confined fluid is transmitted equally in all directions throughout the fluid. This principle forms the foundation for hydraulic systems that multiply force, from car brakes to industrial presses.
Mathematically, Pascal’s principle means that if you apply an additional pressure ΔP at any point in a confined fluid, every other point in the fluid experiences the same pressure increase ΔP.
Hydraulic Systems and Mechanical Advantage
The most important application of Pascal’s principle involves hydraulic systems that provide mechanical advantage. Consider a simple hydraulic lift with two pistons of different areas connected by a fluid-filled tube.
When you apply force F₁ to the smaller piston (area A₁), it creates pressure P₁ = F₁/A₁. According to Pascal’s principle, this same pressure is transmitted to the larger piston (area A₂), creating an output force F₂ = P₁ × A₂.
Since P₁ = P₂, we have:
F₁/A₁ = F₂/A₂
Rearranging: F₂ = F₁ × (A₂/A₁)
If the larger piston has 10 times the area of the smaller piston, you can lift a load 10 times heavier than the force you apply. However, energy conservation still applies – the smaller piston must move 10 times farther than the larger piston moves.

Real-World Physics: Hydraulic systems are everywhere in modern technology. Car brakes use this principle – when you press the brake pedal, a small force is multiplied through hydraulic fluid to create large forces at each wheel. Construction equipment like excavators and bulldozers rely on hydraulic systems to lift massive loads with relatively small input forces.
Buoyancy: The Force That Makes Things Float
Archimedes’ Principle Explained
Archimedes’ principle represents one of physics’ most elegant discoveries: any object partially or completely submerged in a fluid experiences an upward buoyant force equal to the weight of the fluid displaced by the object.
F_buoyant = ρ_fluid × V_displaced × g
Where:
- F_buoyant is the buoyant force (upward)
- ρ_fluid is the density of the fluid
- V_displaced is the volume of fluid displaced by the object
- g is gravitational acceleration
This principle explains not only why objects float or sink, but also why they feel lighter when submerged in fluids. The buoyant force effectively reduces the apparent weight of any submerged object.
Physics Check: A common mistake is thinking that buoyant force depends on the object’s weight or density. In reality, buoyant force depends only on the volume of fluid displaced and the density of the fluid. A steel ball and a ping-pong ball of the same size experience identical buoyant forces when fully submerged in the same fluid.
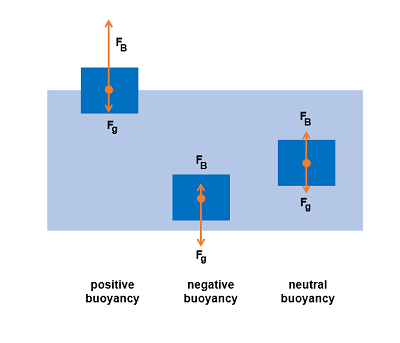
Floating, Sinking, and Neutral Buoyancy
Whether an object floats, sinks, or remains suspended depends on comparing the buoyant force to the object’s weight:
Floating: When ρ_object < ρ_fluid, the object floats with only part of it submerged. The object settles at a depth where the buoyant force equals its weight.
Sinking: When ρ_object > ρ_fluid, the object sinks because its weight exceeds the maximum possible buoyant force (which occurs when completely submerged).
Neutral Buoyancy: When ρ_object = ρ_fluid, the object neither floats nor sinks but remains suspended at any depth.
For floating objects, you can determine what fraction of the object remains submerged using:
Fraction submerged = ρ_object/ρ_fluid
This relationship explains why ice floats with about 90% of its volume underwater (since ice density ≈ 0.9 × water density), and why icebergs pose such navigation hazards with most of their mass hidden below the surface.
Analyzing Complex Buoyancy Situations
Real-world buoyancy problems often involve composite objects or changing conditions. Consider a boat carrying cargo: as you add weight to the boat, it sinks deeper into the water until the increased buoyant force balances the additional weight. If you add too much weight, the boat may sink completely.
For objects with irregular shapes or varying densities, you need to consider the average density and the total volume displaced. A hollow sphere, for example, might have a low average density despite being made of dense material, allowing it to float.
Problem-Solving Strategy: When analyzing buoyancy problems, always identify the forces acting on the object (weight downward, buoyant force upward, and any other applied forces). For floating objects in equilibrium, these forces must balance. For accelerating objects, apply Newton’s second law to find the net force and resulting motion.
Fluid Flow: Understanding How Fluids Move
The Continuity Equation and Flow Rate
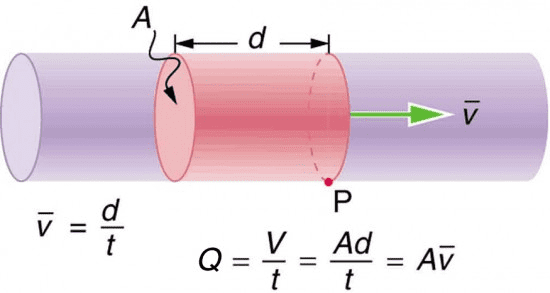
When fluids flow through pipes, channels, or around objects, they follow predictable patterns governed by conservation laws. The continuity equation represents conservation of mass for flowing fluids.
For incompressible fluids (liquids and gases at low speeds), the mass flow rate must remain constant throughout a pipe system. This leads to the continuity equation:
A₁v₁ = A₂v₂ = constant
Where A is the cross-sectional area and v is the fluid velocity at different points in the flow.
This equation tells us that fluid speeds up when flowing through constrictions and slows down when the pipe widens. Think about using your thumb to partially block the end of a garden hose – the water comes out faster through the smaller opening.
The volume flow rate Q = Av remains constant for incompressible flow, measured in cubic meters per second (m³/s) or liters per minute.
Real-World Physics: The continuity equation explains many everyday observations. When you squeeze a shampoo bottle, the liquid flows faster through the small opening. Blood flows more rapidly through the narrow capillaries than through large arteries. Rivers flow faster through narrow channels than wide ones.
Bernoulli’s Equation: Energy Conservation in Fluid Flow
Bernoulli’s equation represents conservation of mechanical energy for flowing fluids. For incompressible, non-viscous flow along a streamline:
P + ½ρv² + ρgh = constant
This equation connects three forms of energy per unit volume:
- Pressure energy (P): energy due to fluid pressure
- Kinetic energy density (½ρv²): energy due to fluid motion
- Gravitational potential energy density (ρgh): energy due to elevation
Bernoulli’s equation reveals that as fluid speed increases, pressure decreases (assuming constant elevation). This counterintuitive relationship forms the basis for understanding airplane lift, venturi meters, and many other applications.
Applications of Bernoulli’s Principle
The most famous application of Bernoulli’s principle involves airplane wing design. Air flowing over the curved upper surface of a wing travels faster than air flowing under the wing, creating lower pressure above the wing and higher pressure below. This pressure difference generates upward lift force.
However, it’s important to note that Bernoulli’s principle alone doesn’t fully explain airplane lift – wing angle and deflection of air downward also contribute significantly to lift generation.
Common Physics Mistake Alert: Many students oversimplify airplane lift as purely a Bernoulli effect. While Bernoulli’s principle contributes to lift, Newton’s third law (air deflected downward creates upward reaction force) plays an equally important role. Modern wing designs rely on both effects working together.
Other applications include:
- Venturi meters for measuring flow rates
- Carburetors mixing fuel and air in engines
- Pitot tubes measuring aircraft airspeed
- Aspirators creating suction for medical and laboratory equipment
Problem-Solving Strategies for Fluid Mechanics
Systematic Approach to Fluid Problems
Fluid mechanics problems can seem overwhelming due to their variety, but following a systematic approach helps ensure success:
- Identify the type of problem: Is it about pressure variation, buoyancy, or fluid flow?
- Draw a clear diagram showing all relevant information, forces, and dimensions
- Choose appropriate principles: Pascal’s principle, Archimedes’ principle, continuity equation, or Bernoulli’s equation
- Define your coordinate system and identify all known and unknown quantities
- Apply conservation laws and fundamental principles step by step
- Check your answer for dimensional consistency and physical reasonableness
Common Problem Types and Approaches
Pressure Problems: Usually involve applying P = P₀ + ρgh or analyzing forces on surfaces in contact with fluids. Remember that pressure acts perpendicular to surfaces and equally in all directions at any point.
Buoyancy Problems: Focus on comparing buoyant force (ρ_fluid × V_displaced × g) with object weight. For floating objects, these forces balance. For submerged objects, consider net force and acceleration.
Flow Problems: Apply continuity equation (A₁v₁ = A₂v₂) for mass conservation and Bernoulli’s equation for energy conservation. Be careful about assumptions like incompressible flow and negligible viscosity.
Estimation and Order-of-Magnitude Reasoning
Developing intuition for fluid mechanics requires practice with estimation. Can you quickly estimate:
- The pressure at the bottom of a swimming pool?
- The buoyant force on a person floating in water?
- The speed of water flowing from a garden hose?
These estimation skills help you catch calculation errors and develop physical intuition that serves you well on the AP exam.
Quick Calculation: At a depth of 10 meters in water, gauge pressure ≈ ρgh = (1000 kg/m³)(10 m/s²)(10 m) = 100,000 Pa ≈ 1 atmosphere. So water pressure doubles every 10 meters of depth!
Laboratory Investigations and Experimental Design
Key Experiments in Fluid Mechanics
Understanding fluid mechanics requires connecting theory with experimental observation. Several classic experiments help students develop deeper insights:
Pressure vs. Depth Investigation: Students can measure pressure at various depths in water using pressure sensors or simple manometers. This investigation reveals the linear relationship between pressure and depth while allowing students to determine fluid density experimentally.
Buoyancy Force Measurement: By measuring the apparent weight of objects when submerged in different fluids, students can verify Archimedes’ principle and investigate how buoyant force depends on fluid density and displaced volume.
Flow Rate and Pipe Diameter Study: Students can investigate how changing pipe diameter affects flow velocity while maintaining constant volume flow rate, providing concrete evidence for the continuity equation.
Designing Your Own Fluid Experiments
When designing fluid mechanics experiments, consider these key factors:
Variables to Control: Temperature affects fluid density and viscosity, so maintain consistent conditions. Ensure clean equipment to minimize unwanted effects from contamination or air bubbles.
Measurement Techniques: Use appropriate precision for your measurements. Pressure measurements might require sensitive gauges, while volume flow rates might be measured by timing how long it takes to fill containers of known volume.
Error Analysis: Consider systematic errors (like calibration issues) and random errors (like measurement precision limits). Understanding uncertainty helps you draw valid conclusions from experimental data.
Real-World Physics: Modern fluid mechanics research uses sophisticated techniques like particle image velocimetry (PIV) to visualize complex flow patterns, and computational fluid dynamics (CFD) to model flows too complex for analytical solutions. These tools help engineers design more efficient airplane wings, automobile bodies, and industrial processes.
Advanced Applications and Current Research
Fluid Mechanics in Biological Systems
Living organisms have evolved remarkable solutions to fluid mechanics challenges. The human circulatory system demonstrates sophisticated applications of pressure gradients, flow regulation, and energy conservation. Your heart acts as a pump creating pressure differences that drive blood flow, while the branching structure of blood vessels optimizes the balance between flow resistance and oxygen delivery.
Bird flight showcases advanced applications of Bernoulli’s principle and flow control. Birds can actively change wing shape and angle to manipulate airflow, achieving flight efficiencies that engineers still struggle to replicate in artificial systems.
Environmental and Engineering Applications
Climate science relies heavily on fluid mechanics to understand atmospheric and oceanic circulation patterns. The principles you’re learning help explain everything from local weather patterns to global climate change.
Modern engineering pushes the boundaries of fluid mechanics in designing more efficient wind turbines, reducing drag on vehicles to improve fuel economy, and developing new medical devices that work with blood flow. Microfluidics – the manipulation of tiny fluid volumes – enables new medical diagnostic devices and drug delivery systems.
Physics Check: The same principles governing large-scale flows (like rivers and atmospheric circulation) also apply to microscopic flows in biological cells and lab-on-a-chip devices. However, at very small scales, effects like surface tension and viscosity become much more important relative to inertial forces.
Common Misconceptions and How to Avoid Them
Pressure Misconceptions
Misconception: “Pressure only acts downward in fluids due to gravity.”
Reality: Pressure in fluids acts equally in all directions at any point. Gravity affects how pressure varies with depth, but doesn’t determine the direction of pressure forces.
Misconception: “Heavier objects experience greater buoyant forces.”
Reality: Buoyant force depends only on the volume of fluid displaced and the fluid density, not on the object’s weight or density.
Flow Misconceptions
Misconception: “Faster-flowing fluids always have higher pressure.”
Reality: Bernoulli’s equation shows that faster-flowing fluids often have lower pressure (at constant elevation). This counterintuitive relationship is key to understanding many applications.
Misconception: “The continuity equation means fluids speed up randomly in pipes.”
Reality: Fluids speed up only when flowing through narrower sections and slow down in wider sections, maintaining constant volume flow rate.
Problem-Solving Misconceptions
Misconception: “Fluid problems require memorizing many different formulas.”
Reality: Most fluid problems use just a few fundamental principles (pressure variation, Archimedes’ principle, continuity, and Bernoulli’s equation) applied systematically.
Practice Problems: Testing Your Understanding
Multiple Choice Practice
Problem 1: A cube with side length 0.2 m and density 800 kg/m³ floats in water (density 1000 kg/m³). What fraction of the cube is submerged?
A) 0.6
B) 0.8
C) 1.0
D) 1.2
Solution: For floating objects, fraction submerged = ρ_object/ρ_fluid = 800/1000 = 0.8. Answer: B
Problem 2: Water flows through a pipe that narrows from diameter 4 cm to diameter 2 cm. If the water speed in the wide section is 2 m/s, what is the speed in the narrow section?
A) 1 m/s
B) 2 m/s
C) 4 m/s
D) 8 m/s
Solution: Using continuity equation A₁v₁ = A₂v₂. Since area depends on diameter squared, A₁/A₂ = (4/2)² = 4. Therefore v₂ = v₁ × (A₁/A₂) = 2 × 4 = 8 m/s. Answer: D
Free Response Practice
Problem 3: A student investigates how pressure varies with depth in a fluid by lowering a pressure sensor into a tank of water. The sensor reads 101,325 Pa at the surface and 111,325 Pa at a depth of 1.0 m.
(a) Calculate the density of the fluid.
(b) Predict the pressure reading at a depth of 2.5 m.
(c) Explain what would happen to the pressure readings if the same experiment were performed in a fluid with half the density.
Solution:
(a) Using P = P₀ + ρgh: 111,325 = 101,325 + ρ(9.8)(1.0)
10,000 = ρ(9.8), so ρ = 1,020 kg/m³
(b) P = 101,325 + (1,020)(9.8)(2.5) = 101,325 + 24,990 = 126,315 Pa
(c) With half the density, pressure increases would be half as large at each depth, so the pressure readings would be between the surface pressure and the original readings.
Experimental Design Challenge
Problem 4: Design an experiment to determine whether the buoyant force on a submerged object depends on the depth of submersion. Include:
- Hypothesis
- Materials needed
- Procedure
- Expected results
- Possible sources of error
Solution Framework:
- Hypothesis: Buoyant force should not depend on depth for fully submerged objects (according to Archimedes’ principle)
- Materials: Scale, string, large container, water, test object, ruler
- Procedure: Measure apparent weight of fully submerged object at various depths
- Expected results: Constant apparent weight (same buoyant force) at all depths
- Error sources: Temperature changes affecting density, air bubbles, measurement precision
Exam Strategies for AP Physics 1 Unit 8
Multiple Choice Strategy
The AP exam tests fluid mechanics through both quantitative calculations and conceptual understanding. For multiple choice questions:
- Read carefully to distinguish between gauge and absolute pressure
- Draw diagrams even for seemingly simple problems
- Check units to catch common calculation errors
- Use process of elimination for conceptual questions
- Don’t panic if a problem seems unfamiliar – apply fundamental principles systematically
Free Response Strategy
Free response questions in fluid mechanics often involve:
- Multi-part scenarios building from simple to complex applications
- Experimental design requiring you to propose investigations or analyze data
- Graphical analysis interpreting pressure, flow, or buoyancy data
- Justification questions requiring clear explanations of physical reasoning
For free response success:
- Start with a clear diagram showing all relevant information
- State your principles explicitly (e.g., “Using Archimedes’ principle…”)
- Show all mathematical work with proper substitution and units
- Connect your answers to physical understanding, not just calculations
- Check reasonableness of numerical answers
Time Management Tips
Fluid mechanics problems can be time-consuming if you get lost in complex setups. Budget your time by:
- Spending extra time on problem setup and diagram drawing
- Using estimation to check if your answers make sense
- Moving on if you get stuck on complex calculations – return later if time allows
- Focusing on partial credit by showing clear reasoning even if calculations are incomplete
Advanced Study Strategies
Connecting Concepts Across Units
Fluid mechanics connects to many other AP Physics 1 topics:
- Forces and Newton’s Laws: Buoyant forces, pressure forces, and fluid resistance
- Energy: Gravitational and kinetic energy in Bernoulli’s equation
- Oscillations: Fluid motion in U-tubes creates simple harmonic motion
- Waves: Understanding how sound travels through fluids
Real-World Problem Solving
Practice applying fluid mechanics to authentic situations:
- Weather phenomena: Why do storm systems rotate? How do pressure differences drive wind?
- Sports applications: Why do curveballs curve? How do swimmers reduce drag?
- Technology: How do hydraulic systems work? Why are airplane wings shaped the way they are?
Mathematical Skills Development
Strengthen your mathematical foundation for fluid mechanics:
- Proportional reasoning: Understanding how changing one variable affects others
- Graphical analysis: Interpreting pressure vs. depth graphs, flow rate diagrams
- Vector analysis: Adding forces in buoyancy problems
- Algebraic manipulation: Solving for unknowns in complex fluid systems
Your Path Forward: From Understanding to Mastery
Mastering fluid mechanics requires more than memorizing equations – it demands developing physical intuition about how fluids behave and confidence in applying fundamental principles to new situations. The concepts you’ve learned in Unit 8 provide a foundation for understanding everything from weather patterns to cardiovascular function, from airplane design to environmental engineering.
As you continue your physics journey, remember that fluid mechanics demonstrates the power of fundamental physical laws to explain and predict complex natural phenomena. The same principles governing water flowing through pipes apply to blood circulation, atmospheric dynamics, and stellar formation. This universality represents one of physics’ most beautiful aspects – simple, elegant laws governing an incredibly diverse range of phenomena.
Key Physics Concepts Summary:
- Pressure acts equally in all directions and increases linearly with depth in static fluids
- Pascal’s principle enables hydraulic systems to multiply force through pressure transmission
- Archimedes’ principle determines buoyant forces based on displaced fluid volume and density
- Continuity equation ensures mass conservation in fluid flow through varying cross-sections
- Bernoulli’s equation represents energy conservation, connecting pressure, velocity, and elevation in flowing fluids
Resources for Continued Learning
Your journey with fluid mechanics doesn’t end with the AP exam. Consider exploring:
- Advanced fluid dynamics in college physics courses
- Computational fluid dynamics for engineering applications
- Biofluids studying circulation in living systems
- Environmental fluid mechanics investigating atmospheric and oceanic flows
- Experimental techniques for visualizing and measuring complex flows
The principles you’ve mastered provide a solid foundation for understanding these advanced topics and their applications to current research and technology development.
Remember, physics is ultimately about understanding the natural world around us. Every time you see water flowing from a faucet, watch an airplane overhead, or feel the resistance when swimming, you’re observing fluid mechanics in action. The equations and principles you’ve learned give you the tools to quantitatively analyze and predict these everyday phenomena – transforming casual observations into deep scientific understanding.
With thorough preparation using the strategies and concepts outlined in this guide, you’re well-equipped to excel on the AP Physics 1 exam and continue exploring the fascinating world of physics beyond the classroom. The combination of conceptual understanding, problem-solving skills, and experimental design experience you’ve developed will serve you well in whatever scientific or technical path you choose to pursue.
Recommended –


1 thought on “Master AP Physics 1 Unit 8: Fluids – The Complete Guide to Pressure, Buoyancy, and Flow”