Mastering AP Physics 1 Unit 2: Force and Translational Dynamics - Your Complete Guide to Acing the Exam

Imagine you’re watching your favorite basketball player drive to the hoop. As they leap into the air, multiple forces act on their body simultaneously – gravity pulls them down, air resistance opposes their motion, and the initial force from their legs propels them forward. This split-second athletic moment perfectly demonstrates the complex world of forces and translational dynamics that governs everything from sports to space exploration.

Welcome to AP Physics 1 Unit 2, where we’ll unravel the fundamental principles that describe how and why objects move. This unit forms the backbone of classical mechanics and connects directly to your everyday experiences, from the simple act of walking to the sophisticated engineering behind electric vehicles and spacecraft.

Learning Objectives: What You’ll Master in This Unit

By the end of this comprehensive guide, you’ll confidently tackle every aspect of force and translational dynamics on the AP Physics 1 exam. Here’s what we’ll cover, aligned with the College Board’s specific learning objectives:

Force Fundamentals: Understanding force as a vector quantity and applying Newton’s laws of motion
Free-Body Diagrams: Creating and analyzing force diagrams for complex scenarios
Contact Forces: Mastering normal force, friction, tension, and spring forces
Motion Analysis: Connecting forces to acceleration and predicting object behavior
Problem-Solving Strategies: Developing systematic approaches to dynamics problems
Real-World Applications: Applying physics principles to engineering and everyday situations

The Foundation: Understanding Force as More Than a Push or Pull

When most students first encounter the concept of force, they think of pushing a door or pulling a rope. While these are valid examples, force in physics represents something much more sophisticated and powerful.

Physics Check: Force is a vector quantity measured in Newtons (N) that describes an interaction between objects. Unlike scalars such as mass or temperature, forces have both magnitude and direction, making them fundamentally different from everyday quantities you might be familiar with.

Force isn’t just about strength – it’s about interaction. Every force involves at least two objects, and according to Newton’s Third Law, forces always come in pairs. When you push against a wall, the wall pushes back against you with equal magnitude but opposite direction. This reciprocal relationship governs everything from molecular interactions to planetary motion.

Types of Forces: The Physics Toolbox

Understanding the different categories of forces helps you identify and analyze complex situations systematically. Let’s explore the main types you’ll encounter in AP Physics 1:

Contact Forces occur when objects physically touch:

Normal Force (N): The perpendicular force exerted by surfaces on objects in contact
Friction Force (f): The parallel force that opposes relative motion between surfaces
Tension Force (T): The pulling force transmitted through strings, ropes, or cables
Applied Force (F_app): Any external force applied to an object

Field Forces act at a distance without physical contact:

Gravitational Force (F_g or W): The attractive force between masses
Electric Force: The force between charged particles (covered in later units)
Magnetic Force: The force on moving charges in magnetic fields (covered in later units)

Newton’s First Law: The Principle of Inertia

Newton’s First Law states that an object at rest stays at rest, and an object in motion stays in motion at constant velocity, unless acted upon by a net external force. This law introduces the crucial concept of inertia – an object’s resistance to changes in its state of motion.

Common Physics Mistake Alert: Many students think that constant motion requires constant force. This misconception comes from everyday experience where friction makes moving objects slow down. In reality, constant velocity requires zero net force!

Real-World Physics: Inertia in Action

Consider riding in a car that suddenly brakes. Your body continues moving forward not because of a mysterious “force,” but because of inertia – your body’s tendency to maintain its state of motion. The seatbelt provides the external force needed to change your motion and keep you safe.

Space missions provide perfect examples of Newton’s First Law in action. Once a spacecraft reaches its desired velocity in the vacuum of space, it can coast for months or years without using fuel, maintaining constant velocity in the absence of significant external forces.

Mathematical Expression and Problem-Solving

Newton’s First Law can be expressed mathematically as:

ΣF = 0 (when acceleration = 0)

This equation tells us that when the sum of all forces acting on an object equals zero, the object either remains at rest or moves with constant velocity. This condition is called equilibrium.

Problem-Solving Strategy: When dealing with First Law problems, always start by identifying all forces acting on the object, then set up equations showing that forces in each direction sum to zero.

Newton’s Second Law: The Heart of Dynamics

Newton’s Second Law provides the quantitative relationship between force, mass, and acceleration:

F_net = ma

This deceptively simple equation contains profound insights about the nature of motion. The net force on an object is directly proportional to its acceleration and inversely related to its mass.

Understanding the Components

Force (F): Measured in Newtons (N), where 1 N = 1 kg⋅m/s²
Mass (m): Measured in kilograms (kg), representing the object’s inertia
Acceleration (a): Measured in m/s², representing the rate of velocity change

The beauty of Newton’s Second Law lies in its universality. Whether you’re analyzing a falling apple, a rocket launch, or the motion of electrons in a computer chip, this same relationship governs the dynamics.

Problem-Solving with Newton’s Second Law

Let’s work through a comprehensive example that demonstrates the systematic approach to Second Law problems:

Example Problem: A 15 kg box is pushed across a horizontal floor with an applied force of 80 N at an angle of 30° above horizontal. The coefficient of kinetic friction between the box and floor is 0.25. Calculate the box’s acceleration.

Step 1: Draw a Free-Body Diagram
Identify all forces acting on the box:

Weight (W = mg) acting downward
Normal force (N) acting upward
Applied force (F_app = 80 N) at 30° above horizontal
Friction force (f_k) opposing motion

Step 2: Choose Coordinate System
Select x-axis along direction of motion, y-axis perpendicular to surface.

Step 3: Break Applied Force into Components
F_app,x = 80 cos(30°) = 80 × 0.866 = 69.3 N
F_app,y = 80 sin(30°) = 80 × 0.500 = 40.0 N

Step 4: Apply Newton’s Second Law in y-direction
Since a_y = 0 (no vertical acceleration):
ΣF_y = 0
N + F_app,y – W = 0
N = W – F_app,y = mg – 40.0 = (15)(9.8) – 40.0 = 107 N

Step 5: Calculate Friction Force
f_k = μ_k × N = 0.25 × 107 = 26.8 N

Step 6: Apply Newton’s Second Law in x-direction
ΣF_x = ma_x
F_app,x – f_k = ma_x
69.3 – 26.8 = 15a_x
a_x = 42.5/15 = 2.83 m/s²

Quick Calculation: The box accelerates at 2.83 m/s² in the positive x-direction.

Newton’s Third Law: Action-Reaction Pairs

Newton’s Third Law states that for every action, there is an equal and opposite reaction. More precisely, when object A exerts a force on object B, object B simultaneously exerts a force on object A that is equal in magnitude but opposite in direction.

Key Characteristics of Action-Reaction Pairs

Equal Magnitude: The forces have identical magnitudes
Opposite Direction: The forces point in exactly opposite directions
Same Type: Both forces are the same type (both gravitational, both normal, etc.)
Different Objects: The forces act on different objects
Simultaneous: The forces exist at the same time

Physics Check: Action-reaction pairs never cancel each other out because they act on different objects. Forces only cancel when they act on the same object.

Real-World Physics: Third Law Applications

Walking: When you walk, you push backward against the ground (action), and the ground pushes forward on you (reaction). Without sufficient friction to provide this reaction force, walking becomes impossible – think about trying to walk on ice!

Rocket Propulsion: Rockets work by expelling hot gases downward at high velocity (action). The gases push back on the rocket with equal force in the opposite direction (reaction), propelling the rocket upward. This principle works in the vacuum of space because no external medium is required.

Swimming: Swimmers push water backward with their hands and feet (action), and the water pushes the swimmer forward (reaction). The effectiveness depends on the swimmer’s technique and the water’s density.

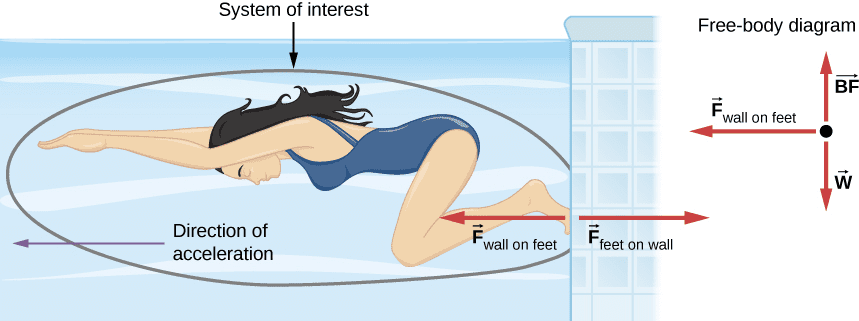
Free-Body Diagrams: Your Problem-Solving Foundation

Free-body diagrams represent the cornerstone of success in AP Physics 1 dynamics problems. These diagrams isolate the object of interest and show all forces acting on it, providing a clear visual foundation for mathematical analysis.

Creating Effective Free-Body Diagrams

Step 1: Isolate the Object
Draw a simple representation of the object (often just a dot or simple shape) separate from its surroundings.

Step 2: Identify All Forces
Systematically consider each interaction:

What surfaces contact the object? (Normal forces, friction)
What pulls on the object? (Tension, gravity)
What pushes the object? (Applied forces)

Step 3: Draw Force Vectors

Use arrows to represent forces
Length indicates relative magnitude
Direction shows force direction
Label each force clearly

Step 4: Choose Coordinate System

Align axes with motion or surface when possible
Maintain consistency throughout the problem

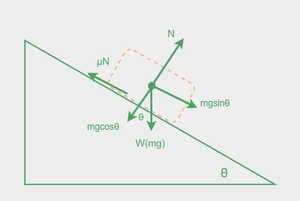
Common Free-Body Diagram Scenarios

Inclined Plane Problems
Objects on inclined planes experience forces that must be resolved into components parallel and perpendicular to the surface. The weight component parallel to the incline (mg sin θ) drives motion down the plane, while the perpendicular component (mg cos θ) determines the normal force.

Connected Objects
When multiple objects are connected by ropes or in contact, create separate free-body diagrams for each object. Remember that tension forces and contact forces follow Newton’s Third Law.

Circular Motion Preview
Although circular motion is covered in detail in Unit 3, objects moving in circles require centripetal forces directed toward the center. Free-body diagrams help identify which forces provide this centripetal acceleration.

Contact Forces: Normal Force and Its Applications

Normal force represents one of the most fundamental contact forces in mechanics. Despite its name suggesting “ordinary,” normal force exhibits complex behavior that often surprises students.

Understanding Normal Force

Normal force is the perpendicular contact force exerted by surfaces on objects. The word “normal” means perpendicular in geometry, not “ordinary” or “typical.” This force adjusts automatically to prevent objects from penetrating surfaces.

Key Normal Force Principles:

Always perpendicular to the contact surface
Magnitude adjusts to maintain contact (within limits)
Cannot pull – only pushes away from surfaces
Varies with surface orientation and other forces

Normal Force in Different Situations

Horizontal Surfaces
On horizontal surfaces, normal force typically equals the object’s weight:
N = mg (when no vertical acceleration exists)

However, normal force can differ from weight when:

Other vertical forces act on the object
The object accelerates vertically
The surface itself accelerates

Inclined Surfaces
On inclined planes, normal force equals the component of weight perpendicular to the surface:
N = mg cos θ

This relationship explains why objects feel “lighter” on steep inclines and why friction decreases on slippery slopes.

Physics Check: Normal force is not always equal to weight! This common misconception leads to errors in problems involving vertical forces or accelerating reference frames.

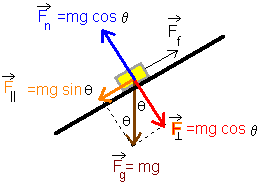
Friction: The Force That Makes Motion Possible

Friction might seem like an obstacle to motion, but it’s actually essential for most everyday activities. Without friction, you couldn’t walk, cars couldn’t turn, and fasteners wouldn’t hold objects together.

Types of Friction

Static Friction (f_s): Prevents motion between stationary surfaces

Acts to oppose potential motion
Magnitude adjusts up to maximum value: f_s,max = μ_s N
Direction opposes the applied force trying to cause motion

Kinetic Friction (f_k): Opposes motion between sliding surfaces

Constant magnitude: f_k = μ_k N
Direction opposes actual motion
Typically less than maximum static friction: μ_k < μ_s

Friction Coefficients and Surface Properties

Friction coefficients (μ) are dimensionless quantities that depend on surface materials and conditions:

μ_s: Coefficient of static friction
μ_k: Coefficient of kinetic friction

Common coefficient ranges:

Rubber on concrete: μ_s ≈ 1.0, μ_k ≈ 0.7
Steel on steel: μ_s ≈ 0.6, μ_k ≈ 0.4
Ice on ice: μ_s ≈ 0.1, μ_k ≈ 0.03

Real-World Physics: Anti-lock braking systems (ABS) in cars work by preventing wheels from locking up and sliding. Static friction between tires and road provides much greater stopping force than kinetic friction, which occurs when wheels slide.

Problem-Solving with Friction

Friction problems require careful analysis of motion state:

Static Situation: Object not moving

f_s ≤ μ_s N (friction adjusts to maintain equilibrium)
Check if applied force exceeds f_s,max

Kinetic Situation: Object sliding

f_k = μ_k N (constant friction force)
Apply Newton’s Second Law with known friction

Example Problem: A 25 kg crate sits on a horizontal floor with μ_s = 0.4 and μ_k = 0.3. What horizontal force is needed to:
a) Just start the crate moving?
b) Keep it moving at constant velocity?

Solution:
a) To start motion: F_app = f_s,max = μ_s N = μ_s mg = 0.4 × 25 × 9.8 = 98 N
b) For constant velocity: F_app = f_k = μ_k N = μ_k mg = 0.3 × 25 × 9.8 = 73.5 N

Tension Force: Connecting Objects Through Strings and Ropes

Tension force transmits forces through flexible connectors like strings, ropes, and cables. Understanding tension is crucial for analyzing systems with pulleys, hanging objects, and connected masses.

Properties of Tension Force

Direction: Always pulls along the string/rope direction
Magnitude: Uniform throughout ideal strings (massless, inextensible)
Transmission: Efficiently transfers forces over distances
Constraints: Creates motion constraints between connected objects

Analyzing Tension in Different Systems

Single Hanging Object
For an object hanging vertically in equilibrium:
T = mg (tension equals weight)

Angled Support Systems
When strings support objects at angles, resolve tensions into components and apply equilibrium conditions.

Connected Objects on Surfaces
Objects connected by strings over pulleys create systems where tensions provide coupling forces between the objects.

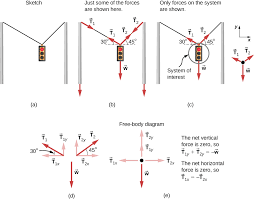
Advanced Tension Analysis: Pulley Systems

Pulley systems redirect tension forces and can provide mechanical advantage. For ideal pulleys (massless, frictionless):

Tension is constant throughout the rope
Acceleration magnitudes are related by rope constraints
Multiple pulleys can multiply forces

Problem-Solving Strategy: For pulley problems, draw separate free-body diagrams for each mass, identify tension forces, establish acceleration relationships, and solve the resulting system of equations.

Springs and Elastic Forces: Hooke’s Law in Action

Spring forces demonstrate how materials respond elastically to deformation. Hooke’s Law provides the mathematical relationship governing these forces and connects directly to oscillatory motion covered in later units.

Hooke’s Law Fundamentals

F_spring = -kx

Where:

F_spring: Spring force (N)
k: Spring constant (N/m)
x: Displacement from equilibrium position (m)
Negative sign indicates restoring force direction

Understanding Spring Constants

The spring constant k characterizes a spring’s stiffness:

Large k: Stiff spring (requires more force for same displacement)
Small k: Soft spring (requires less force for same displacement)
Units: N/m (force per unit displacement)

Spring constants depend on:

Material properties (Young’s modulus)
Wire diameter and coil geometry
Number of active coils

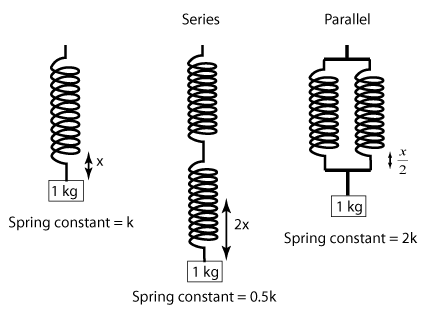
Springs in Series and Parallel

Series Configuration (springs end-to-end):

Same force through each spring
Displacements add: x_total = x_1 + x_2
Equivalent spring constant: 1/k_eq = 1/k_1 + 1/k_2

Parallel Configuration (springs side-by-side):

Same displacement for each spring
Forces add: F_total = F_1 + F_2
Equivalent spring constant: k_eq = k_1 + k_2

Physics Check: Springs in series become softer (smaller k_eq), while springs in parallel become stiffer (larger k_eq). This is opposite to electrical resistors!

Applying Newton’s Laws: Systematic Problem-Solving Approach

Success in AP Physics 1 dynamics problems requires a systematic methodology that ensures you don’t miss crucial steps or make computational errors.

The Universal Problem-Solving Method

Step 1: Understand the Problem

Read carefully and identify what’s given and what’s asked
Visualize the physical situation
Identify the objects and interactions involved

Step 2: Draw and Label Diagrams

Create clear free-body diagrams for each object
Include coordinate systems
Label all forces with appropriate symbols

Step 3: Apply Physics Principles

Write Newton’s laws in component form
Include constraint equations (ropes, contact conditions)
Apply conservation principles when applicable

Step 4: Solve Mathematically

Set up equation systems
Solve algebraically before substituting numbers
Check dimensional consistency

Step 5: Evaluate and Interpret

Check if answers make physical sense
Consider limiting cases
Relate back to the original question

Common Problem Categories and Strategies

Equilibrium Problems

ΣF = 0 in all directions
Often involve multiple objects and constraint forces
Systematic component analysis essential

Constant Acceleration Problems

Apply F_net = ma along with kinematic equations
Consider initial conditions and time dependence
Connect forces to resulting motion

Connected Objects Problems

Separate free-body diagrams for each object
Identify constraint relationships
Solve coupled equation systems

Inclined Plane Problems

Choose coordinate system aligned with incline
Resolve weight into parallel and perpendicular components
Consider friction effects carefully

Real-World Applications: Engineering and Technology Connections

Understanding force and dynamics principles enables innovation in countless technological applications. Let’s explore how these concepts drive modern engineering solutions.

Transportation Technology

Automotive Safety Systems
Modern cars incorporate numerous physics principles for safety:

Crumple zones extend collision time, reducing peak forces (F = Δp/Δt)
Airbags increase contact area and time, distributing forces
Seat belts provide constraint forces during sudden deceleration

Aerospace Engineering
Spacecraft design requires careful force analysis:

Launch vehicles overcome gravitational forces through thrust
Orbital mechanics balance gravitational and centripetal forces
Re-entry systems manage extreme deceleration forces

Sports Science and Human Performance

Athletic Performance Analysis
Physics principles explain and optimize athletic performance:

Jumping mechanics: Ground reaction forces determine jump height
Running efficiency: Friction forces enable forward propulsion
Equipment design: Materials science creates better sporting goods

Biomechanics Applications
Understanding forces in biological systems:

Joint forces during movement affect injury risk
Muscle force production determines strength capabilities
Prosthetic design must replicate natural force transmission

Advanced Topics: Preview of Future Concepts

Unit 2 provides the foundation for more advanced physics concepts you’ll encounter later in AP Physics 1 and beyond.

Circular Motion Connection

The force concepts learned here directly apply to circular motion analysis:

Centripetal force requirements for circular paths
Banking angle optimization for vehicle turns
Satellite orbital mechanics combining gravitational and centripetal forces

Energy and Momentum Links

Forces connect directly to energy and momentum concepts:

Work-energy theorem relates forces to energy changes
Impulse-momentum theorem connects forces to momentum changes
Conservation principles emerge from Newton’s laws

Wave and Oscillation Foundations

Spring forces introduce oscillatory motion concepts:

Simple harmonic motion governed by restoring forces
Resonance phenomena in mechanical systems
Wave propagation through elastic media

Practice Problems: AP Exam Preparation

Let’s work through representative problems that demonstrate the types of questions you’ll encounter on the AP Physics 1 exam.

Multiple Choice Practice

Question 1: A 5.0 kg block is pulled across a horizontal surface by a force of 20 N applied at 37° above horizontal. If the coefficient of kinetic friction is 0.30, what is the magnitude of the acceleration?

A) 1.2 m/s² B) 2.4 m/s² C) 3.2 m/s² D) 4.0 m/s²

Solution Approach:

Draw free-body diagram with all forces
Resolve applied force: F_x = 20 cos(37°) = 16 N, F_y = 20 sin(37°) = 12 N
Find normal force: N = mg – F_y = 49 – 12 = 37 N
Calculate friction: f_k = 0.30 × 37 = 11.1 N
Apply Newton’s second law: ma = F_x – f_k = 16 – 11.1 = 4.9 N
Find acceleration: a = 4.9/5.0 = 0.98 ≈ 1.0 m/s²

Answer: A) 1.2 m/s² (closest to calculated value)

Free Response Practice

Question 2: A system consists of two blocks connected by a light string over a massless, frictionless pulley. Block A (mass m_A = 3.0 kg) rests on a horizontal surface with coefficient of kinetic friction μ_k = 0.25. Block B (mass m_B = 2.0 kg) hangs vertically.

a) Draw free-body diagrams for both blocks
b) Determine the acceleration of the system
c) Calculate the tension in the string
d) If the string breaks, describe the subsequent motion of each block

Solution:

Part a: Free-body diagrams

Block A: Weight (down), Normal force (up), Tension (right), Friction (left)
Block B: Weight (down), Tension (up)

Part b: System acceleration
For Block A: T – f_k = m_A a, where f_k = μ_k m_A g = 0.25 × 3.0 × 9.8 = 7.35 N
For Block B: m_B g – T = m_B a

Combining equations: m_B g – μ_k m_A g = (m_A + m_B)a
a = (2.0 × 9.8 – 7.35)/(3.0 + 2.0) = 12.25/5.0 = 2.45 m/s²

Part c: String tension
T = m_B g – m_B a = 2.0 × 9.8 – 2.0 × 2.45 = 19.6 – 4.9 = 14.7 N

Part d: Motion after string breaks

Block A: Decelerates due to friction at a = -μ_k g = -2.45 m/s²
Block B: Falls freely with acceleration g = 9.8 m/s²

Experimental Design Question

Question 3: Design an experiment to determine the coefficient of static friction between a wooden block and various surfaces.

Required Elements:

Equipment list and setup diagram
Procedure with specific measurements
Data analysis method
Sources of uncertainty and error minimization

Sample Response:

Equipment: Wooden block, digital scale, various surface materials, protractor, adjustable inclined plane

Setup: Place surface material on adjustable incline, position block on surface

Procedure:

Measure block mass using digital scale
Gradually increase incline angle until block just begins to slide
Record critical angle θ_c for each surface material
Repeat measurements 5 times for each surface
Calculate average critical angle for each surface

Data Analysis:
At the critical angle: mg sin θ_c = μ_s mg cos θ_c
Therefore: μ_s = tan θ_c

Uncertainty Considerations:

Angle measurement precision (±0.5°)
Consistent starting conditions
Observer reaction time for motion detection
Surface contamination effects

[INSERT DIAGRAM: Experimental setup showing inclined plane with protractor, block positioning, and measurement points clearly labeled]

Common Mistakes and How to Avoid Them

Learning from typical student errors accelerates your mastery of dynamics concepts and improves exam performance.

Conceptual Mistakes

Mistake 1: Confusing mass and weight

Error: Using mass and weight interchangeably
Correction: Weight is force (W = mg), mass is property (measured in kg)
Prevention: Always use correct units and distinguish between m and mg

Mistake 2: Misapplying Newton’s Third Law

Error: Thinking action-reaction pairs cancel each other
Correction: Action-reaction pairs act on different objects
Prevention: Identify which object each force acts upon

Mistake 3: Assuming normal force equals weight

Error: Writing N = mg in all situations
Correction: N = mg only on horizontal surfaces with no vertical acceleration
Prevention: Always analyze vertical force equilibrium

Mathematical Mistakes

Mistake 4: Incorrect vector component resolution

Error: Using wrong trigonometric functions for components
Correction: Adjacent side uses cosine, opposite side uses sine
Prevention: Draw clear diagrams with angle definitions

Mistake 5: Sign errors in equations

Error: Inconsistent positive/negative direction conventions
Correction: Define coordinate system clearly and stick to it
Prevention: Check that accelerations and forces have consistent signs

Mistake 6: Unit confusion

Error: Mixing different unit systems (pounds with kilograms)
Correction: Convert all quantities to consistent SI units
Prevention: Include units in all calculations and check dimensional analysis

Common Physics Mistake Alert: Always check if your numerical answer makes physical sense. If you calculate that a person can jump 50 meters high, reconsider your approach!

Memory Techniques and Study Strategies

Effective physics learning requires both conceptual understanding and practical problem-solving skills. Here are proven strategies for mastering dynamics.

Conceptual Memory Aids

Newton’s Laws Mnemonics:

First Law: “Inertia = I Never Eat Rapidly, Thus I Always Stay”
Second Law: “Force Makes Acceleration” (F = ma)
Third Law: “Actions Always React” (equal and opposite)

Force Type Categories:

Contact: “Can Touch” (Normal, Friction, Tension, Applied)
Field: “Far Away” (Gravitational, Electric, Magnetic)

Problem-Solving Memory Techniques

Free-Body Diagram Checklist:

Isolate the object
Draw all forces
Establish coordinates
Apply Newton’s laws
Remember: “I.D.E.A.”

Equation Organization:
Create formula sheets organized by situation type:

Equilibrium problems: ΣF = 0
Constant acceleration: F_net = ma
Friction problems: f ≤ μN
Spring problems: F = -kx

Exam Strategies and Test-Taking Tips

AP Physics 1 success requires both content mastery and strategic test-taking approaches.

Multiple Choice Strategy

Time Management: Allocate approximately 1.5 minutes per question

Quick conceptual questions: 30-45 seconds
Calculation problems: 2-3 minutes
Complex scenarios: 3-4 minutes

Elimination Techniques:

Check units for dimensional consistency
Use limiting cases to eliminate unreasonable answers
Consider physical reasonableness of numerical values

Common Trap Avoidance:

Read questions carefully for key words like “magnitude,” “direction,” “maximum”
Don’t confuse similar-looking equations (F = ma vs. a = F/m)
Watch for vector vs. scalar distinctions

Free Response Strategy

Organization: Use clear section headings and logical flow

Part (a): Show setup and initial analysis
Part (b): Present calculations with units
Part (c): Interpret results physically

Partial Credit Maximization:

Show all work even for incorrect final answers
Include free-body diagrams when relevant
Explain reasoning in words, not just equations

Time Allocation: Budget approximately 20-25 minutes per free response question

5 minutes: Reading and planning
15 minutes: Solving and writing
5 minutes: Checking and finalizing

Calculator and Formula Sheet Usage

Effective Calculator Use:

Store intermediate results to avoid rounding errors
Use scientific notation for very large or small numbers
Double-check entries for calculation-heavy problems

Formula Sheet Strategy:

Familiarize yourself with provided equations before the exam
Know which equations apply to specific situations
Remember that derivations may be required for unlisted relationships

Connections to Other AP Physics 1 Units

Understanding how Unit 2 connects to other course content strengthens your overall physics comprehension and exam performance.

Unit 1 (Kinematics) Integration

Force and motion are intimately connected through Newton’s Second Law:

Acceleration from kinematics becomes the link to forces
Motion graphs help predict force requirements
Projectile motion involves gravitational force throughout flight

Quick Calculation: If you know acceleration from kinematics analysis, you can find net force using F_net = ma. If you know forces, you can predict acceleration and use kinematic equations to find motion details.

Unit 3 (Circular Motion) Foundation

The force concepts developed here directly enable circular motion analysis:

Centripetal force emerges from Newton’s Second Law applied to circular paths
Banking problems combine normal force, weight, and friction
Satellite motion balances gravitational force with centripetal force requirements

Unit 4 (Energy) Relationships

Forces and energy connect through the work-energy theorem:

Conservative forces (gravity, springs) store potential energy
Non-conservative forces (friction) dissipate mechanical energy
Power relates force, velocity, and energy transfer rates

Unit 5 (Momentum) Links

Newton’s laws provide the foundation for momentum concepts:

Impulse-momentum theorem derives from F = ma and kinematics
Conservation of momentum emerges from Newton’s Third Law
Collision analysis requires force understanding during brief interactions

Technology Integration and Modern Applications

Contemporary technology provides fascinating applications of dynamics principles and offers new ways to explore physics concepts.

Simulation and Modeling Tools

PhET Simulations: Interactive online tools for visualizing forces and motion

Forces and Motion: Basics: Explore applied forces, friction, and motion
The Ramp: Investigate inclined plane dynamics with adjustable parameters
Masses and Springs: Study Hooke’s Law and oscillatory behavior

Video Analysis Software: Tools like Logger Pro or Tracker enable analysis of real motion

Record sports activities and analyze forces
Study collision dynamics frame by frame
Measure acceleration and compare to theoretical predictions

Modern Engineering Applications

Autonomous Vehicles: Self-driving cars use dynamics principles for:

Path planning: Calculating required forces for safe turns
Collision avoidance: Predicting stopping distances based on friction
Stability control: Managing forces during emergency maneuvers

Robotics: Industrial and consumer robots apply force control for:

Precise manipulation: Controlling grip forces on delicate objects
Dynamic balance: Maintaining stability during rapid movements
Force feedback: Sensing interaction forces with environment

Space Technology: Modern spacecraft missions showcase dynamics principles:

Ion propulsion: Low-force, high-efficiency propulsion systems
Gravity assists: Using planetary gravity for trajectory changes
Station keeping: Maintaining orbital positions through small force adjustments

Assessment and Self-Evaluation

Regular self-assessment helps identify strengths and areas needing improvement throughout your Unit 2 studies.

Conclusion: Mastering Force and Dynamics for AP Success

You’ve now explored the comprehensive world of force and translational dynamics that forms the foundation of classical mechanics. From Newton’s fundamental laws to complex multi-object systems, these concepts govern everything from the simple act of walking to the sophisticated engineering behind space exploration.

The key to success in AP Physics 1 Unit 2 lies in developing both conceptual understanding and systematic problem-solving skills. Remember that physics is not about memorizing formulas – it’s about understanding the fundamental principles that describe how our universe works and applying these principles to solve real-world problems.

Final Physics Wisdom

Remember that physics is fundamentally about curiosity and understanding. Every time you see a sports highlight, experience a car ride, or watch a rocket launch, you’re witnessing the principles you’ve learned in action. This connection between abstract concepts and tangible experiences makes physics both challenging and remarkably rewarding.

The systematic problem-solving approach you’ve developed here will serve you well throughout the AP Physics 1 course and beyond. Whether you pursue engineering, medicine, research, or any other field, the analytical thinking skills and physical intuition you’ve gained will prove invaluable.

Keep practicing, stay curious, and remember that every physics expert was once a beginner working through their first free-body diagram. You now have the tools and knowledge to tackle any dynamics problem with confidence and precision.

Physics Check: The journey of mastering physics is like learning to see the hidden machinery that makes our world work. Once you understand forces and motion, you’ll never look at moving objects the same way again.

Good luck with your AP Physics 1 studies, and remember – the force is now with you to succeed on exam day and beyond!

This comprehensive guide represents hundreds of hours of teaching experience and has been crafted specifically for AP Physics 1 students. Keep this resource handy throughout your studies, and return to specific sections as needed while working through problems and preparing for assessments.

Recommended –