Picture this: You’re watching your favorite basketball player launch a perfect three-pointer. The ball traces a beautiful arc through the air, defying gravity for a moment before swishing through the net. Or maybe you’re riding in a car, watching the speedometer climb as you merge onto the highway, feeling your body press back into the seat. These everyday experiences aren’t just random events – they’re perfect examples of kinematics, the branch of physics that describes motion without worrying about what causes it.
As an AP Physics 1 student, Unit 1: Kinematics is your gateway into the world of physics. This isn’t just about memorizing equations or drawing graphs – it’s about developing a physicist’s way of thinking about motion. Whether you’re analyzing a sprinter’s acceleration out of the blocks or understanding why GPS satellites need relativistic corrections, the concepts you master in kinematics will form the foundation for everything else you’ll learn in physics.
Many students find kinematics challenging because it requires a new way of thinking about familiar experiences. You’ve been moving your entire life, but now you need to describe that motion mathematically and graphically. Don’t worry – by the end of this guide, you’ll not only understand kinematics but also develop the problem-solving skills that will serve you throughout AP Physics 1 and beyond.
What You Need to Master
By the end of Unit 1, you should confidently demonstrate understanding of these College Board learning objectives:
LO 3.A.1: Express the motion of an object using narrative, mathematical, and graphical representations
LO 3.A.2: Analyze experimental data describing the motion of an object and express the results using narrative, mathematical, and graphical representations
LO 3.A.3: Predict the motion of an object subject to various types of forces using kinematic equations
LO 3.A.4: Analyze scenarios and make predictions about the motion of an object that experiences forces over a time interval using the impulse-momentum theorem
Essential Knowledge Areas:
- Position, velocity, and acceleration as vector quantities
- Graphical analysis of motion
- Kinematic equations for constant acceleration
- Free fall and projectile motion
- Relative motion concepts
Chapter 1: Understanding Motion – From Intuition to Physics
When you walk to class, your brain automatically calculates dozens of motion-related decisions. You adjust your speed to avoid collisions, predict where moving objects will be, and coordinate complex movements without conscious thought. Physics takes this intuitive understanding and makes it precise and predictable.
What is Kinematics?
Kinematics is the mathematical description of motion without considering the forces that cause it. Think of it as the “what” of motion rather than the “why.” We describe motion using three fundamental quantities: position, velocity, and acceleration.
The Power of Mathematical Description
Why do we need math to describe something as simple as walking? Because precise mathematical descriptions allow us to make accurate predictions. NASA doesn’t launch rockets based on “it looks about right” – they use kinematic equations to calculate exact trajectories.
Real-World Physics: Modern smartphones use accelerometers and gyroscopes to track motion for everything from fitness apps to augmented reality games. These devices rely on the same kinematic principles you’re learning to provide accurate motion sensing.
Coordinate Systems and Reference Frames
Before we can describe motion, we need to establish a reference frame – a coordinate system from which we measure position and motion. This choice is crucial because motion is always relative to something else.
Key Physics Concepts:
- Motion is always described relative to a chosen reference frame
- Coordinate systems provide the mathematical framework for describing position
- The choice of reference frame can simplify or complicate problem-solving
- Vector quantities have both magnitude and direction
Chapter 2: Position, Displacement, and Distance – Where Are You Going?
Understanding the difference between position, displacement, and distance is crucial for kinematics success. These concepts seem simple but contain subtleties that often trip up students on the AP exam.
Position (x)
Position tells you where an object is located relative to your chosen origin. It’s a vector quantity, meaning it has both magnitude and direction. On a number line, position can be positive or negative depending on which side of the origin you’re on.
Displacement (Δx)
Displacement is the change in position – it’s where you end up minus where you started:
Δx = x_final – x_initial
Displacement is also a vector quantity. If you walk 10 meters east, then 6 meters west, your displacement is 4 meters east, not 16 meters.
Distance
Distance is the total path length traveled, regardless of direction. It’s always positive and is a scalar quantity. In the example above, you traveled a total distance of 16 meters.

Common Physics Mistake Alert: Students often confuse distance and displacement. Remember: displacement is the shortest path between two points (straight line), while distance is the actual path traveled. For motion problems, displacement is usually more important because it’s what appears in kinematic equations.
Mathematical Relationships
For motion in one dimension:
- Average position: x_avg = (x_initial + x_final)/2
- Displacement: Δx = x_final – x_initial
- Distance ≥ |displacement| (distance is always greater than or equal to the magnitude of displacement)
Physics Check: A student walks 5 m north, then 3 m south, then 2 m north. What are the total distance and displacement?
Answer: Total distance = 5 + 3 + 2 = 10 m; Displacement = 5 – 3 + 2 = 4 m north
Key Physics Concepts:
- Position is location relative to an origin
- Displacement is change in position (vector quantity)
- Distance is total path length (scalar quantity)
- Displacement appears in kinematic equations, not distance
Chapter 3: Velocity – How Fast and Which Way?
Velocity is one of the most important concepts in kinematics, yet it’s frequently misunderstood. Many students think velocity and speed are the same thing – they’re not, and this distinction is crucial for AP Physics 1 success.
Average Velocity
Average velocity is displacement divided by time interval:
v_avg = Δx/Δt = (x_final – x_initial)/(t_final – t_initial)
Notice that we use displacement, not distance. This means average velocity can be zero even if you’ve been moving the entire time. If you drive around the block and return to your starting point, your average velocity is zero regardless of how fast you drove.
Instantaneous Velocity
Instantaneous velocity is the velocity at a specific moment in time. Mathematically, it’s the limit of average velocity as the time interval approaches zero:
v = lim(Δt→0) Δx/Δt = dx/dt
Don’t worry if you haven’t learned calculus yet – for AP Physics 1, you can think of instantaneous velocity as the slope of a position-time graph at any point.
Speed vs. Velocity
Speed is the magnitude of velocity – it tells you how fast something is moving but not which direction. Velocity includes both speed and direction information.
Speed = |velocity| (speed is always positive)
Velocity = speed with direction (velocity can be positive or negative)
Real-World Physics: Car speedometers show speed, not velocity. GPS navigation systems, however, need to track velocity (speed and direction) to provide accurate directions and arrival time estimates.
Vector Nature of Velocity
In one dimension, we represent direction using positive and negative signs:
- Positive velocity: motion in the positive direction
- Negative velocity: motion in the negative direction
- Zero velocity: object is at rest (momentarily)
Problem-Solving Strategy: Velocity Calculations
- Identify initial and final positions
- Calculate displacement (Δx = x_final – x_initial)
- Identify time interval (Δt = t_final – t_initial)
- Apply average velocity formula: v_avg = Δx/Δt
- Check units and sign (direction)
Physics Check: A car travels from position x = 20 m to x = -10 m in 5 seconds. What is its average velocity?
Answer: v_avg = (-10 – 20)/(5 – 0) = -30/5 = -6 m/s (negative indicates motion in negative direction)
Key Physics Concepts:
- Average velocity = displacement/time (not distance/time)
- Instantaneous velocity is the slope of position-time graphs
- Velocity is a vector; speed is a scalar
- Velocity can be negative, zero, or positive
Chapter 4: Acceleration – The Rate of Change of Motion
Acceleration is where many students start to struggle with kinematics, partly because our everyday understanding of acceleration doesn’t match the physics definition. In physics, acceleration occurs whenever velocity changes – whether that’s speeding up, slowing down, or changing direction.
Average Acceleration
Average acceleration is the change in velocity divided by the time interval:
a_avg = Δv/Δt = (v_final – v_initial)/(t_final – t_initial)
Instantaneous Acceleration
Instantaneous acceleration is the acceleration at a specific moment, mathematically defined as:
a = lim(Δt→0) Δv/Δt = dv/dt
For AP Physics 1, think of instantaneous acceleration as the slope of a velocity-time graph.
Types of Acceleration
- Positive acceleration: Velocity becoming more positive (could be speeding up in positive direction or slowing down in negative direction)
- Negative acceleration: Velocity becoming more negative (could be slowing down in positive direction or speeding up in negative direction)
- Zero acceleration: Constant velocity (could be at rest or moving at constant speed)
Common Physics Mistake Alert: “Negative acceleration” doesn’t always mean “slowing down,” and “positive acceleration” doesn’t always mean “speeding up.” The sign of acceleration tells you about the direction of acceleration relative to your coordinate system, not whether the object is speeding up or slowing down.
Determining if an Object is Speeding Up or Slowing Down
- Speeding up: Velocity and acceleration have the same sign
- Slowing down: Velocity and acceleration have opposite signs
Examples:
- v = +10 m/s, a = +3 m/s²: Speeding up (both positive)
- v = +10 m/s, a = -3 m/s²: Slowing down (opposite signs)
- v = -10 m/s, a = -3 m/s²: Speeding up (both negative)
- v = -10 m/s, a = +3 m/s²: Slowing down (opposite signs)
Units and Dimensional Analysis
Acceleration has units of m/s², which means “meters per second per second.” This tells you how many m/s the velocity changes each second.
Problem-Solving Strategy: Acceleration Problems
- Identify initial and final velocities
- Identify time interval
- Apply acceleration formula: a = Δv/Δt
- Check units (should be m/s²)
- Interpret the sign (direction of acceleration)
- Determine if object is speeding up or slowing down
Physics Check: A car’s velocity changes from +15 m/s to +5 m/s in 2 seconds. What is its acceleration?
Answer: a = (5 – 15)/(2 – 0) = -10/2 = -5 m/s²
The negative acceleration means the car is slowing down (velocity and acceleration have opposite signs).
Key Physics Concepts:
- Acceleration is change in velocity over time
- Acceleration can be positive, negative, or zero
- The sign of acceleration indicates direction, not speeding up/slowing down
- Objects speed up when velocity and acceleration have the same sign
Chapter 5: Motion Graphs – The Visual Language of Physics
Graphs are the visual language of physics, and mastering motion graphs is essential for AP Physics 1 success. These graphs don’t just display data – they tell stories about motion and allow you to extract quantitative information through mathematical analysis.
Position-Time Graphs
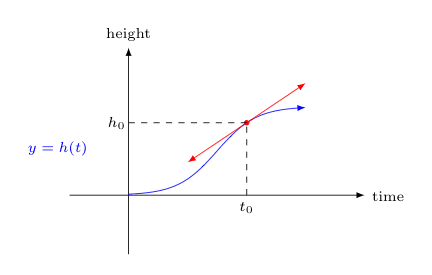
Position-time graphs show how an object’s position changes over time. The key insight is that the slope of a position-time graph gives you velocity.
Reading Position-Time Graphs:
- Slope = velocity: Steeper slope means higher speed
- Positive slope: Motion in positive direction
- Negative slope: Motion in negative direction
- Zero slope: Object at rest
- Curved line: Changing velocity (acceleration present)
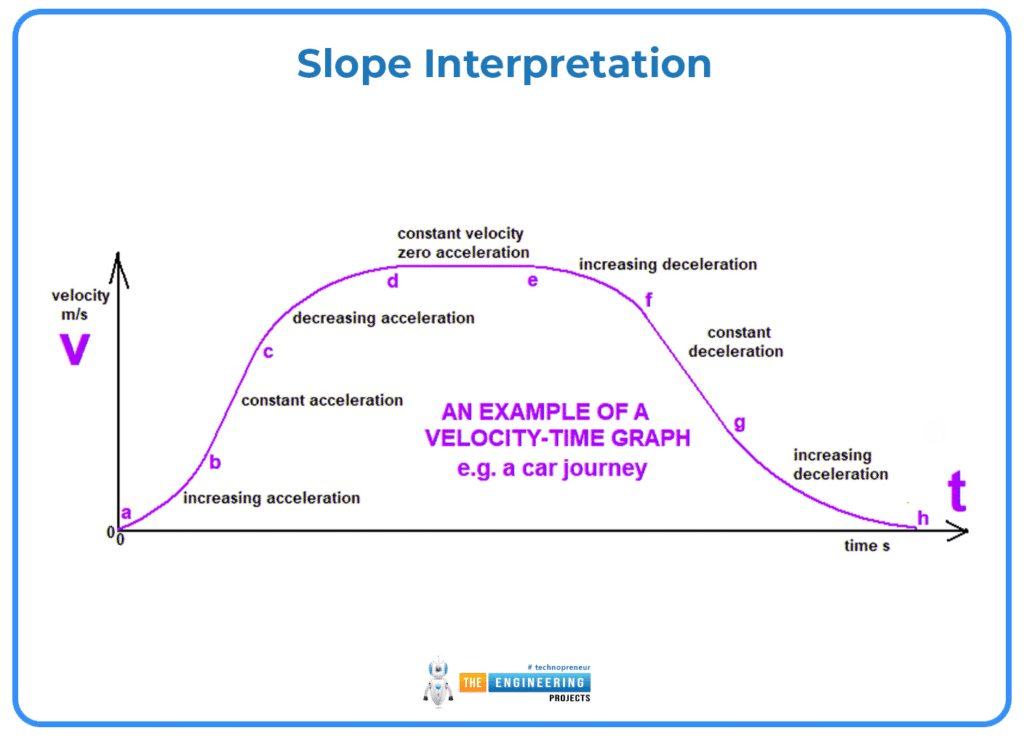
Velocity-Time Graphs
Velocity-time graphs show how velocity changes over time. Two crucial relationships:
- Slope = acceleration
- Area under the curve = displacement
Reading Velocity-Time Graphs:
- Horizontal line: Constant velocity (zero acceleration)
- Positive slope: Positive acceleration
- Negative slope: Negative acceleration
- Area above time axis: Positive displacement
- Area below time axis: Negative displacement
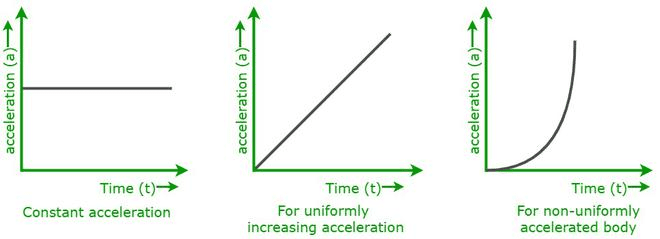
Acceleration-Time Graphs
Acceleration-time graphs show how acceleration changes over time. The area under an acceleration-time curve gives you the change in velocity.
Real-World Physics: Modern cars use accelerometers to detect crashes and deploy airbags. These sensors create real-time acceleration-time graphs, and when the acceleration exceeds certain thresholds, safety systems activate.
Graph Analysis Strategies
- Identify what each axis represents (position, velocity, or acceleration vs. time)
- Look for patterns: straight lines (constant rate) vs. curves (changing rate)
- Calculate slopes and areas to extract quantitative information
- Connect graphs: if you have position vs. time, you can construct velocity vs. time
Problem-Solving Strategy: Graph Analysis
- Identify the type of graph (x-t, v-t, or a-t)
- Determine what information you need (position, velocity, acceleration, displacement)
- Use appropriate relationship (slope or area)
- Calculate numerical values
- Include proper units and signs
Physics Check: On a velocity-time graph, what does the area between t = 2s and t = 5s represent if the velocity is constant at 8 m/s?
Answer: Area = base × height = (5-2) s × 8 m/s = 24 m. This represents the displacement during that time interval.
Common Graph Mistakes to Avoid:
- Confusing slope and area calculations
- Forgetting that area below the time axis is negative
- Mixing up which type of graph you’re analyzing
- Not including proper units in calculations
Key Physics Concepts:
- Position-time graph slope = velocity
- Velocity-time graph slope = acceleration
- Velocity-time graph area = displacement
- Acceleration-time graph area = change in velocity
The Kinematic Equations – Your Problem-Solving Toolkit
The kinematic equations are your most powerful tools for solving motion problems with constant acceleration. These equations aren’t just formulas to memorize – they’re mathematical relationships that describe how position, velocity, acceleration, and time are connected.
The Big Four Kinematic Equations
For motion with constant acceleration, we have four fundamental equations:
- v = v₀ + at (velocity as a function of time)
- x = x₀ + v₀t + ½at² (position as a function of time)
- v² = v₀² + 2a(x – x₀) (velocity-position relationship)
- x = x₀ + ½(v₀ + v)t (average velocity relationship)
Understanding Each Equation
Equation 1: v = v₀ + at
This equation tells you how velocity changes with time under constant acceleration. If acceleration is zero, velocity remains constant. If acceleration is positive, velocity increases linearly with time.
Equation 2: x = x₀ + v₀t + ½at²
This is the “master equation” for position. It accounts for initial position, motion due to initial velocity, and additional displacement due to acceleration. The ½at² term represents the extra distance covered due to acceleration.
Equation 3: v² = v₀² + 2a(x – x₀)
This equation is invaluable when you don’t know time. It directly relates velocity to position and acceleration. Notice that it involves velocity squared, which is why speeds can’t exceed certain limits in many physical situations.
Equation 4: x = x₀ + ½(v₀ + v)t
This equation uses the average velocity concept. Since velocity changes linearly with constant acceleration, the average velocity is simply (v₀ + v)/2.
Choosing the Right Equation
The key to success is identifying which variables you know and which you need to find:
- Know a, v₀, t; need v: Use equation 1
- Know v₀, a, t; need x: Use equation 2
- Know v₀, v, a; need x: Use equation 3
- Know v₀, v, t; need x: Use equation 4
Problem-Solving Strategy: Kinematic Problems
- Draw a diagram showing the situation
- Choose a coordinate system and clearly define positive direction
- List known values with proper signs and units
- Identify what you need to find
- Select the appropriate kinematic equation
- Substitute values and solve
- Check your answer for reasonableness
Sample Problem: The Accelerating Car
A car starts from rest and accelerates at 3.0 m/s² for 5.0 seconds. How far does it travel?
Solution:
- Given: v₀ = 0 m/s, a = 3.0 m/s², t = 5.0 s
- Find: x (displacement)
- Choose equation 2: x = x₀ + v₀t + ½at²
- Assuming x₀ = 0: x = 0 + (0)(5.0) + ½(3.0)(5.0)²
- x = 0 + 0 + ½(3.0)(25) = 37.5 m
Real-World Physics: These same equations govern the motion of everything from electrons in particle accelerators to spacecraft traveling to Mars. NASA mission planners use kinematic equations to calculate precise trajectories for interplanetary missions.
Physics Check: A ball is thrown upward with an initial velocity of 20 m/s. How high does it go? (Use g = 10 m/s²)
Answer: At maximum height, v = 0. Using v² = v₀² + 2a(x – x₀):
0² = 20² + 2(-10)(x – 0)
0 = 400 – 20x
x = 20 m
Key Physics Concepts:
- Kinematic equations apply only to constant acceleration
- Choose equations based on known and unknown variables
- Always include signs (directions) in your calculations
- Check answers for physical reasonableness
Free Fall – When Gravity Takes Over
Free fall is one of the most important applications of kinematics, and it’s frequently tested on the AP Physics 1 exam. Understanding free fall helps you master both the mathematical and conceptual aspects of accelerated motion.
What is Free Fall?
Free fall occurs when the only force acting on an object is gravity. In this idealized situation, all objects experience the same acceleration regardless of their mass – a profound insight that revolutionized our understanding of motion.
The Acceleration Due to Gravity
Near Earth’s surface, the acceleration due to gravity is approximately:
g = 9.8 m/s² (or 10 m/s² for simplified calculations)
This acceleration is always directed toward the center of the Earth (downward in everyday terms).
Sign Conventions for Free Fall
Choosing your coordinate system is crucial for free fall problems:
Option 1: Up is positive
- g = -9.8 m/s² (acceleration is downward)
- Upward velocities are positive
- Downward velocities are negative
Option 2: Down is positive
- g = +9.8 m/s² (acceleration is downward)
- Downward velocities are positive
- Upward velocities are negative
Both conventions work – just be consistent throughout each problem!
Key Insights About Free Fall
Time Symmetry: For an object thrown straight up, the time to reach maximum height equals the time to fall back to the starting level.
Speed Symmetry: An object returns to its starting height with the same speed it had initially (but opposite direction).
Independence of Mass: In the absence of air resistance, all objects fall with the same acceleration regardless of their mass.
Sample Problem: The Thrown Ball
A ball is thrown straight up with an initial velocity of 15 m/s from a height of 2.0 m. How long does it take to hit the ground?
Solution:
Using the coordinate system where up is positive:
- v₀ = +15 m/s
- a = g = -9.8 m/s²
- x₀ = +2.0 m
- x = 0 m (ground level)
Using x = x₀ + v₀t + ½at²:
0 = 2.0 + 15t + ½(-9.8)t²
0 = 2.0 + 15t – 4.9t²
4.9t² – 15t – 2.0 = 0
Using the quadratic formula:
t = [15 ± √(225 + 39.2)]/9.8 = [15 ± 16.25]/9.8
Taking the positive solution: t = 3.19 s
Common Physics Mistake Alert: Students often forget that objects in free fall continue to accelerate even after they reach maximum height. The acceleration is always -g (if up is positive), whether the object is moving up, at rest at the peak, or moving down.
Real-World Applications
- Skydiving and parachute design
- Spacecraft reentry calculations
- Sports analysis (basketball shots, high jump)
- Safety engineering (airbag timing, construction site safety)
Physics Check: A stone is dropped from rest. After 3 seconds, what is its velocity and how far has it fallen?
Answer: v = v₀ + gt = 0 + (9.8)(3) = 29.4 m/s downward
x = ½gt² = ½(9.8)(3)² = 44.1 m
Key Physics Concepts:
- All objects in free fall have acceleration g = 9.8 m/s²
- Mass doesn’t affect free fall motion (ignoring air resistance)
- Free fall problems use standard kinematic equations with a = ±g
- Sign conventions must be consistent throughout problems
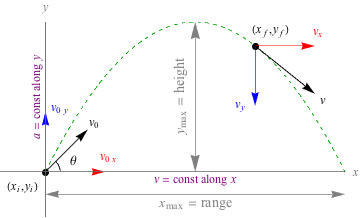
Projectile Motion – Motion in Two Dimensions
Projectile motion combines everything you’ve learned about one-dimensional kinematics and extends it to two dimensions. This topic is heavily tested on the AP Physics 1 exam and provides excellent practice for vector analysis.
Key Principle: Independence of Motion
The horizontal and vertical components of projectile motion are independent of each other. This means you can analyze them separately using one-dimensional kinematics principles.
Horizontal Motion:
- No acceleration (assuming no air resistance)
- Constant velocity: vₓ = v₀ₓ = v₀ cos θ
- Position: x = x₀ + v₀ₓt
Vertical Motion:
- Constant acceleration due to gravity: aᵧ = -g
- Initial velocity: v₀ᵧ = v₀ sin θ
- Velocity: vᵧ = v₀ᵧ – gt
- Position: y = y₀ + v₀ᵧt – ½gt²
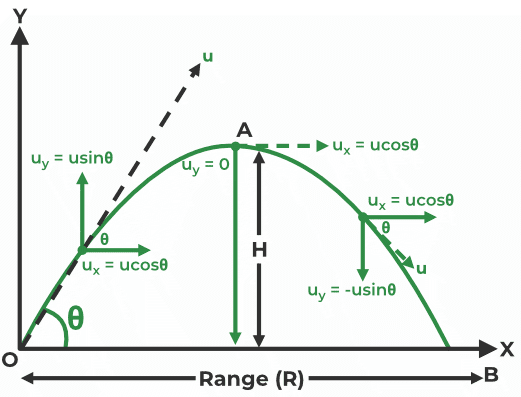
Analyzing Projectile Motion
Launch Angle and Initial Velocity Components
For a projectile launched at angle θ with initial speed v₀:
- v₀ₓ = v₀ cos θ (horizontal component)
- v₀ᵧ = v₀ sin θ (vertical component)
Key Projectile Motion Equations
- Time of flight: t = 2v₀ sin θ/g (for level ground)
- Maximum height: H = (v₀ sin θ)²/(2g)
- Range: R = v₀² sin(2θ)/g (for level ground)
Problem-Solving Strategy: Projectile Motion
- Identify the motion type (projectile motion)
- Set up coordinate system (usually x horizontal, y vertical with up positive)
- Find initial velocity components (v₀ₓ and v₀ᵧ)
- Analyze horizontal and vertical motions separately
- Use kinematic equations for each dimension
- Combine results as needed
Sample Problem: The Cannon Ball
A cannon fires a ball at 45° with an initial speed of 50 m/s. Find the maximum height and range.
Solution:
Initial velocity components:
- v₀ₓ = 50 cos(45°) = 50(0.707) = 35.4 m/s
- v₀ᵧ = 50 sin(45°) = 50(0.707) = 35.4 m/s
Maximum height (when vᵧ = 0):
Using v² = v₀² + 2aΔy:
0² = (35.4)² + 2(-9.8)H
H = (35.4)²/(2 × 9.8) = 64.0 m
Time of flight:
t = 2v₀ᵧ/g = 2(35.4)/9.8 = 7.22 s
Range:
R = v₀ₓ × t = 35.4 × 7.22 = 256 m
Real-World Physics: Video game physics engines use projectile motion equations to create realistic ballistics. Whether you’re playing basketball games or combat simulations, the trajectories you see are calculated using the same physics you’re learning.
Special Cases in Projectile Motion
Horizontal Launch: When θ = 0°
- v₀ₓ = v₀, v₀ᵧ = 0
- Time depends only on height: t = √(2h/g)
- Range: R = v₀√(2h/g)
Maximum Range: Occurs at θ = 45° for level ground
- This angle gives equal horizontal and vertical velocity components
- Range formula simplifies to R = v₀²/g
Physics Check: A ball is thrown horizontally from a 20 m high cliff with speed 15 m/s. How far from the base of the cliff does it land?
Answer: Time to fall: t = √(2h/g) = √(2×20/9.8) = 2.02 s
Horizontal distance: x = v₀ₓt = 15 × 2.02 = 30.3 m
Key Physics Concepts:
- Horizontal and vertical motions are independent
- Horizontal motion has constant velocity (no acceleration)
- Vertical motion has constant acceleration (gravity)
- Maximum range occurs at 45° launch angle
Relative Motion – It’s All About Perspective
Relative motion is a concept that challenges our everyday intuitions about motion. The velocity you measure for an object depends entirely on your reference frame – your perspective from which you’re observing the motion.
The Principle of Relativity
All motion is relative to a chosen reference frame. There’s no such thing as absolute motion – only motion relative to something else. This principle, first clearly articulated by Galileo, revolutionized our understanding of motion and laid the groundwork for Einstein’s theory of relativity.
Relative Velocity
If object A moves with velocity vₐ relative to reference frame C, and object B moves with velocity vᵦ relative to the same frame C, then the velocity of A relative to B is:
vₐᵦ = vₐ – vᵦ
This equation works in one dimension with proper attention to signs.

Vector Addition for Relative Motion
In two dimensions, relative velocities add as vectors:
v⃗ₐc = v⃗ₐᵦ + v⃗ᵦc
Where:
- v⃗ₐc is velocity of A relative to C
- v⃗ₐᵦ is velocity of A relative to B
- v⃗ᵦc is velocity of B relative to C
Common Relative Motion Scenarios
River Crossing Problems
A boat crossing a river must account for the river’s current. The boat’s velocity relative to the ground is the vector sum of its velocity relative to the water and the water’s velocity relative to the ground.
Moving Walkway Problems
When you walk on a moving walkway, your velocity relative to the ground is the sum of your walking velocity relative to the walkway and the walkway’s velocity relative to the ground.
Sample Problem: The River Crossing
A boat can travel at 5.0 m/s in still water. It attempts to cross a river that flows at 3.0 m/s. If the boat heads directly across the river, what is its actual velocity relative to the shore?
Solution:
The boat’s velocity has two components:
- Across the river: 5.0 m/s
- Downstream (due to current): 3.0 m/s
The resultant velocity magnitude:
|v| = √[(5.0)² + (3.0)²] = √[25 + 9] = √34 = 5.83 m/s
Direction: θ = tan⁻¹(3.0/5.0) = 31° downstream from straight across
Real-World Physics: GPS systems must account for relative motion between satellites, Earth’s rotation, and your movement to provide accurate position information. Air traffic control systems constantly calculate relative velocities to maintain safe aircraft separation.
Problem-Solving Strategy: Relative Motion
- Identify all reference frames involved in the problem
- Choose a primary reference frame (usually ground or lab frame)
- Draw vector diagrams showing all velocities
- Apply vector addition/subtraction as appropriate
- Calculate magnitude and direction of resultant vectors
Physics Check: Car A travels east at 60 km/h and Car B travels west at 40 km/h. What is the velocity of Car A relative to Car B?
Answer: Choosing east as positive: vₐ = +60 km/h, vᵦ = -40 km/h
vₐᵦ = vₐ – vᵦ = 60 – (-40) = 100 km/h east
Key Physics Concepts:
- All motion is relative to a chosen reference frame
- Relative velocities add/subtract as vectors
- The observer’s motion affects measured velocities
- Vector addition is essential for two-dimensional relative motion
Practice Problems and Exam Strategies
Now let’s test your understanding with problems that mirror the AP Physics 1 exam format and difficulty level.
Multiple Choice Questions
Question 1: A ball is thrown straight up with an initial velocity of 20 m/s. What is its velocity when it returns to its starting height?
A) 0 m/s
B) 10 m/s downward
C) 20 m/s downward
D) 20 m/s upward
Answer: C) 20 m/s downward
Explanation: Due to energy conservation and symmetry in free fall, the ball returns to its starting height with the same speed but opposite direction.
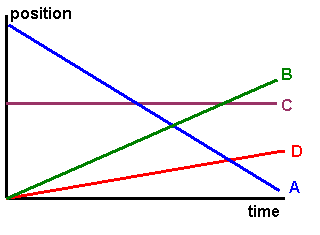
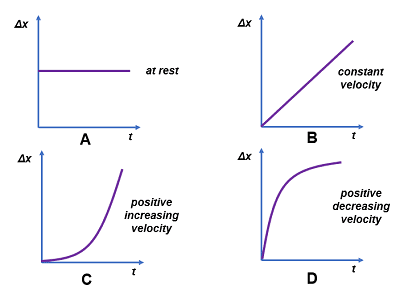
Question 2: Which of the following graphs best represents the motion of an object with constant positive acceleration?
[THIS IS FIGURE: Four velocity-time graphs labeled A-D showing different relationships]
Answer: The graph showing a straight line with positive slope
Explanation: Constant acceleration produces a linear relationship between velocity and time, with the slope equal to the acceleration value.
Question 3: A projectile is launched at 30° above horizontal with speed v₀. Which expression gives the time to reach maximum height?
A) v₀/(g sin 30°)
B) (v₀ sin 30°)/g
C) v₀/(g cos 30°)
D) (v₀ cos 30°)/g
Answer: B) (v₀ sin 30°)/g
Explanation: At maximum height, vertical velocity is zero. Using v = v₀ + at: 0 = v₀ sin 30° – gt, so t = (v₀ sin 30°)/g.
Free Response Questions
Question 4: A car accelerates from rest at a constant rate of 2.0 m/s² for 8.0 seconds, then maintains constant velocity for 6.0 seconds, then decelerates at -3.0 m/s² until it stops.
(a) Draw velocity-time and acceleration-time graphs for the entire motion.
(b) Calculate the total distance traveled.
(c) Find the total time for the motion.
Sample Solution:
(a) [INSERT DIAGRAM: Two graphs – velocity-time showing three phases (acceleration, constant velocity, deceleration) and acceleration-time showing corresponding constant acceleration values]
(b) Distance calculation:
- Phase 1 (acceleration): v = at = 2.0 × 8.0 = 16 m/s
Distance: x₁ = ½at² = ½(2.0)(8.0)² = 64 m - Phase 2 (constant velocity): x₂ = vt = 16 × 6.0 = 96 m
- Phase 3 (deceleration): Time to stop: t = v/|a| = 16/3.0 = 5.33 s
Distance: x₃ = vt – ½at² = 16(5.33) – ½(3.0)(5.33)² = 42.7 m - Total distance: 64 + 96 + 42.7 = 203 m
(c) Total time: 8.0 + 6.0 + 5.33 = 19.3 s
Data Analysis Questions
Question 5: The following data was collected for a ball rolling down a ramp:
| Time (s) | Position (m) |
|---|---|
| 0.0 | 0.0 |
| 1.0 | 1.2 |
| 2.0 | 4.8 |
| 3.0 | 10.8 |
| 4.0 | 19.2 |
(a) Determine if the motion has constant acceleration.
(b) Calculate the acceleration.
(c) Predict the position at t = 5.0 s.
Solution:
(a) For constant acceleration, position should follow x = ½at². Let’s check if x/t² is constant:
- t = 1.0 s: x/t² = 1.2/1.0 = 1.2
- t = 2.0 s: x/t² = 4.8/4.0 = 1.2
- t = 3.0 s: x/t² = 10.8/9.0 = 1.2
- t = 4.0 s: x/t² = 19.2/16.0 = 1.2
Since x/t² is constant, the motion has constant acceleration.
(b) From x = ½at², we get a = 2x/t². Using any data point:
a = 2(1.2)/1.0² = 2.4 m/s²
(c) At t = 5.0 s: x = ½(2.4)(5.0)² = 30.0 m
Experimental Design Questions
Question 6: Design an experiment to measure the acceleration due to gravity using a simple pendulum or falling object setup.
Sample Response Framework:
- Hypothesis: Objects in free fall experience constant acceleration g ≈ 9.8 m/s²
- Materials: Stopwatch, meter stick, small dense object, release mechanism
- Procedure: Drop object from known heights, measure fall times, repeat for multiple heights
- Data Collection: Record height and time for each trial
- Analysis: Plot h vs. t² graph; slope should equal ½g
- Sources of Error: Air resistance, reaction time, measurement precision
- Improvements: Use photogate timers, vacuum chamber, multiple trials
Study Strategies and Exam Tips
Formula Sheet and Reference Materials
Essential Kinematic Equations:
- v = v₀ + at
- x = x₀ + v₀t + ½at²
- v² = v₀² + 2a(x – x₀)
- x = x₀ + ½(v₀ + v)t
Key Relationships:
- Average velocity = Δx/Δt
- Average acceleration = Δv/Δt
- Slope of x-t graph = velocity
- Slope of v-t graph = acceleration
- Area under v-t graph = displacement
Constants:
- g = 9.8 m/s² (acceleration due to gravity)
Final Thoughts and Next Steps
Mastering kinematics requires both conceptual understanding and mathematical problem-solving skills. The motion concepts you’ve learned here appear throughout physics and engineering, from analyzing car crashes to designing spacecraft trajectories.
Immediate Action Items:
- Complete all practice problems in this guide
- Create summary sheets for each major topic
- Form study groups to discuss challenging concepts
- Take timed practice tests to build exam confidence
Long-Term Success Strategies:
- Review kinematic concepts before starting each new unit
- Connect new physics topics back to motion principles
- Practice FRQ writing using kinematic examples
- Seek additional help if you’re struggling with any concepts
Remember that physics is ultimately about understanding how the natural world works. Every time you see motion – from a bouncing ball to a soaring airplane – you now have the mathematical tools to describe and predict that motion precisely.
The problem-solving skills and analytical thinking you develop in kinematics will serve you well beyond AP Physics 1. Whether you pursue engineering, medicine, research, or any technical field, the ability to analyze complex problems systematically is invaluable.
Keep practicing, stay curious about the world around you, and remember that mastering physics takes time and persistence. You’re building skills that will last a lifetime!
Recommended –


3 thoughts on “AP Physics 1 Unit 1: Kinematics – The Complete Student Guide to Motion (2025)”