Introduction to Chemical Kinetics
Have you ever wondered why some chemical reactions happen in milliseconds while others take years? Why does milk spoil faster at room temperature than in the refrigerator? Or how enzymes in your body can speed up reactions by millions of times? Welcome to the fascinating world of chemical kinetics – the study of reaction rates and the factors that influence them.
AP Chemistry Unit 5: Kinetics represents approximately 7-9% of your AP exam and is arguably one of the most practical units in the entire course. Unlike thermodynamics (which tells us if a reaction will occur), kinetics tells us how fast it will happen and how it happens at the molecular level.
Why Kinetics Matters
Understanding chemical kinetics is crucial for:
- Industrial chemistry: Optimizing reaction conditions for maximum efficiency
- Environmental science: Understanding pollution degradation rates
- Medicine: Drug metabolism and effectiveness
- Food science: Preservation and spoilage prevention
- Materials science: Polymer formation and degradation
This comprehensive guide will take you from basic rate concepts to advanced reaction mechanisms, preparing you not just for the AP exam but for a deeper understanding of how chemical reactions actually work.
Quick Reference Guide
At-a-Glance Information
Unit Weight: 7-9% of AP Chemistry Exam
Key Topics: 11 major topics (5.1-5.11)
Essential Skills: Graph analysis, mathematical relationships, mechanism interpretation
Common Question Types: Rate law determination, graph interpretation, mechanism analysis
Must-Know Formulas
| Concept | Formula | Variables |
|---|---|---|
| Rate Expression | Rate = -Δ[A]/Δt = +Δ[B]/Δt | [A] = concentration, t = time |
| Rate Law | Rate = k[A]^m[B]^n | k = rate constant, m,n = orders |
| First-Order | ln[A] = ln[A]₀ – kt | [A]₀ = initial concentration |
| Second-Order | 1/[A] = 1/[A]₀ + kt | k = rate constant |
| Half-Life (1st order) | t₁/₂ = 0.693/k | Independent of concentration |
| Arrhenius | k = Ae^(-Ea/RT) | A = frequency factor, Ea = activation energy |
Key Graphs to Recognize
- Zero Order: [A] vs t → linear
- First Order: ln[A] vs t → linear
- Second Order: 1/[A] vs t → linear
- Energy Profile: Energy vs reaction coordinate
Reaction Rates Fundamentals
Defining Reaction Rate
The rate of a chemical reaction is defined as the change in concentration of a reactant or product per unit time. For a general reaction:
aA + bB → cC + dDThe rate can be expressed as:
Rate = -1/a × Δ[A]/Δt = -1/b × Δ[B]/Δt = +1/c × Δ[C]/Δt = +1/d × Δ[D]/ΔtKey Points:
- Negative sign for reactants (concentrations decrease)
- Positive sign for products (concentrations increase)
- Stoichiometric coefficients ensure all expressions give the same rate
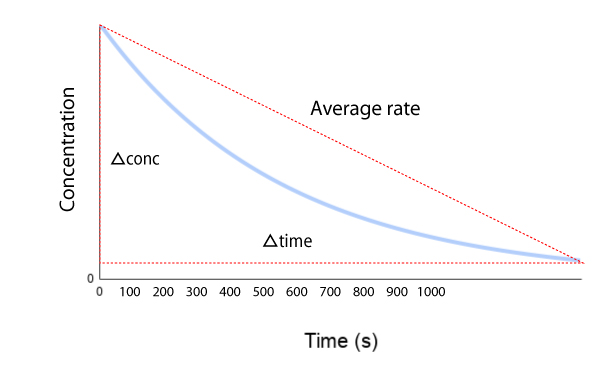
Types of Reaction Rates
- Average Rate: Change over a finite time interval
Average Rate = Δ[A]/Δt- Instantaneous Rate: Rate at a specific moment (slope of tangent)
Instantaneous Rate = d[A]/dt- Initial Rate: Instantaneous rate at t = 0
- Most commonly used in experiments
- Avoids complications from reverse reactions
Factors Affecting Reaction Rate
Understanding what influences reaction rates is crucial for both theoretical knowledge and practical applications.
1. Concentration
- Higher concentration → More particles → More collisions → Faster rate
- This relationship is quantified in the rate law
2. Temperature
- Higher temperature → More kinetic energy → More effective collisions → Faster rate
- Rule of thumb: 10°C increase often doubles reaction rate
3. Surface Area
- Greater surface area → More contact between reactants → Faster rate
- Particularly important for heterogeneous reactions
4. Catalysts
- Catalysts provide alternative pathways with lower activation energy
- Increase rate without being consumed
5. Nature of Reactants
- Bond strength and molecular complexity affect reaction rates
- Ionic reactions generally faster than covalent bond breaking/forming
Rate Laws and Reaction Order
Understanding Rate Laws
The rate law expresses the relationship between reaction rate and reactant concentrations:
Rate = k[A]^m[B]^nWhere:
- k = rate constant (temperature dependent)
- m, n = reaction orders (must be determined experimentally)
- m + n = overall reaction order
Determining Reaction Order
Method 1: Initial Rates Method
Compare experiments where only one concentration changes:
Analysis:
- Experiments 1 & 2: [A] doubles, rate increases 4× → Order in A = 2
- Experiments 1 & 3: [B] doubles, rate doubles → Order in B = 1
- Rate law: Rate = k[A]²[B]
Method 2: Graphical Analysis
Using integrated rate laws to determine order from concentration vs. time data.
Rate Constant Units
The units of k depend on the overall reaction order:
| Overall Order | Units of k |
|---|---|
| 0 | M·s⁻¹ |
| 1 | s⁻¹ |
| 2 | M⁻¹·s⁻¹ |
| 3 | M⁻²·s⁻¹ |
| n | M¹⁻ⁿ·s⁻¹ |
Integrated Rate Laws and Graphs
The Power of Integrated Rate Laws
While differential rate laws tell us the rate at any moment, integrated rate laws relate concentration to time, allowing us to:
- Predict concentrations at any time
- Determine reaction order from experimental data
- Calculate half-lives
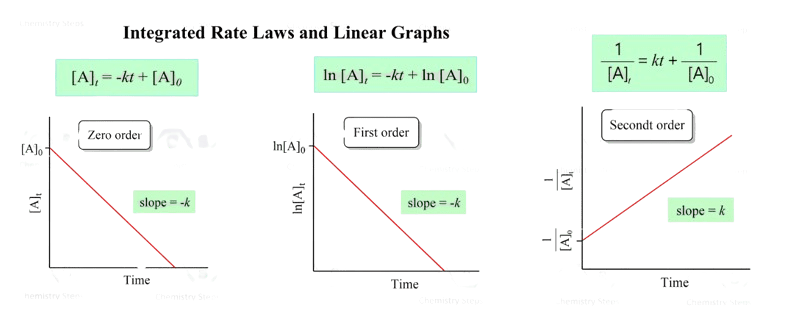
Zero-Order Reactions
Integrated Rate Law: [A] = [A]₀ – kt
Characteristics:
- Constant rate regardless of concentration
- Linear plot: [A] vs t
- Half-life: t₁/₂ = [A]₀/2k (depends on initial concentration)
- Example: Surface catalyzed reactions when surface is saturated
Key Point: Zero-order kinetics often observed when reaction rate is limited by factors other than reactant concentration (e.g., enzyme saturation).
First-Order Reactions
Integrated Rate Law: ln[A] = ln[A]₀ – kt
Characteristics:
- Rate proportional to concentration: Rate = k[A]
- Linear plot: ln[A] vs t (slope = -k)
- Half-life: t₁/₂ = 0.693/k (constant, independent of concentration)
- Examples: Radioactive decay, many decomposition reactions
Half-Life Derivation:
At t₁/₂: [A] = [A]₀/2
ln([A]₀/2) = ln[A]₀ - kt₁/₂
ln(1/2) = -kt₁/₂
t₁/₂ = ln(2)/k = 0.693/kSecond-Order Reactions
Integrated Rate Law: 1/[A] = 1/[A]₀ + kt
Characteristics:
- Rate proportional to concentration squared: Rate = k[A]²
- Linear plot: 1/[A] vs t (slope = k)
- Half-life: t₁/₂ = 1/(k[A]₀) (depends on initial concentration)
- Examples: Bimolecular elementary reactions
Graphical Method for Order Determination
To determine reaction order from concentration-time data:
- Plot [A] vs t: If linear → zero order
- Plot ln[A] vs t: If linear → first order
- Plot 1/[A] vs t: If linear → second order
Pro Tip: The plot that gives the best linear relationship (highest R²) indicates the correct order.
Elementary Reactions and Collision Theory
Elementary Reactions
An elementary reaction occurs in a single step at the molecular level. For elementary reactions, the rate law can be written directly from the stoichiometry:
Elementary: A + B → Products
Rate Law: Rate = k[A][B]Important Distinction:
- Elementary reactions: Rate law matches stoichiometry
- Overall reactions: Rate law must be determined experimentally
Molecularity
Molecularity is the number of molecules that participate in an elementary reaction:
- Unimolecular: A → Products (e.g., radioactive decay)
- Bimolecular: A + B → Products or 2A → Products
- Termolecular: A + B + C → Products (very rare)
Why are termolecular reactions rare? The probability of three molecules colliding simultaneously with proper orientation and sufficient energy is extremely low.
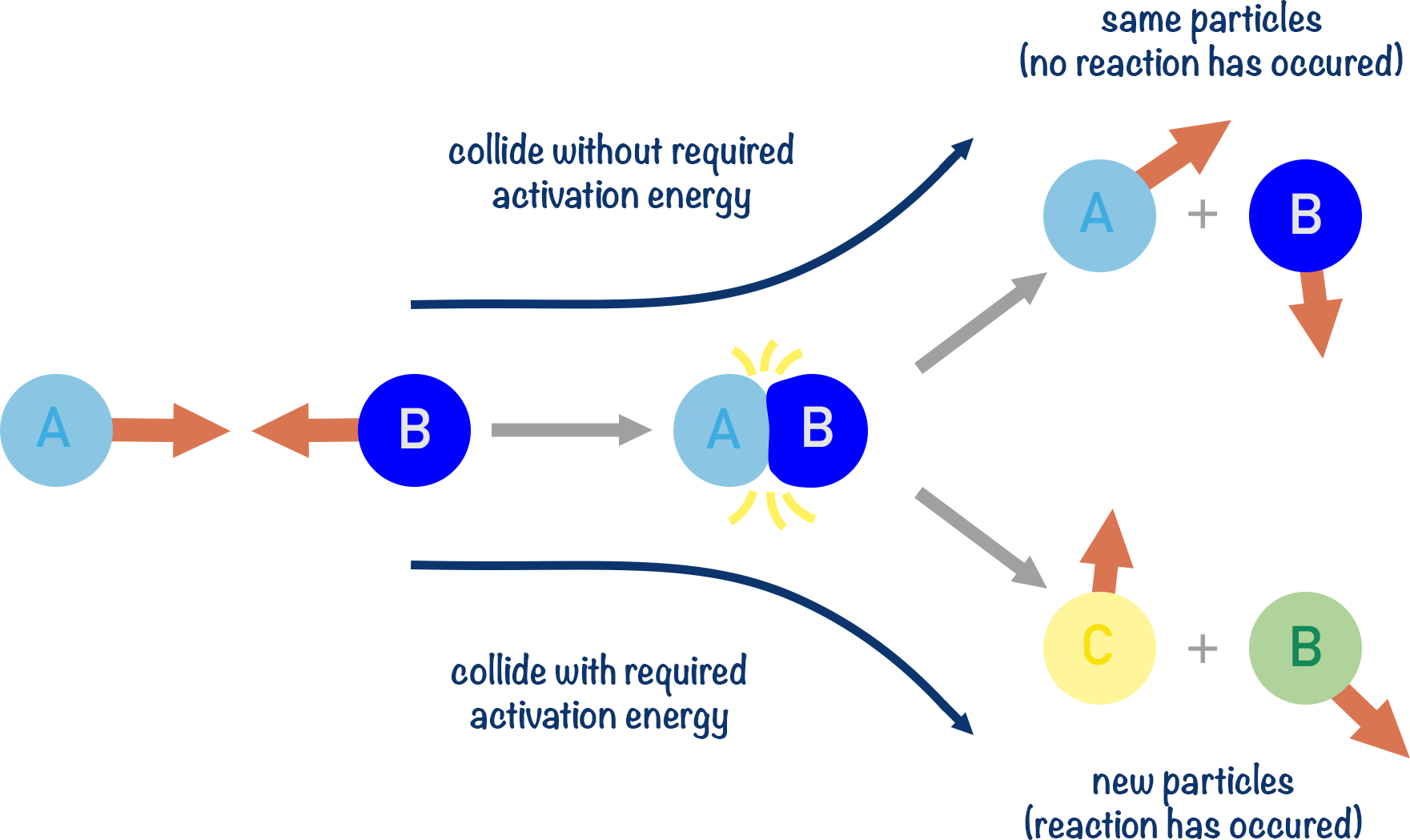
Collision Theory
For a reaction to occur, molecules must:
- Collide with sufficient energy
- Collide with proper orientation
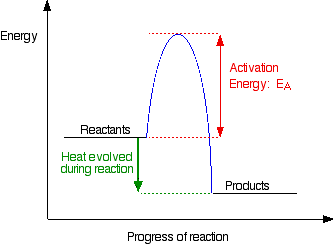
Activation Energy (Ea)
Activation energy is the minimum energy required for a reaction to occur. It represents the energy barrier that must be overcome.
Key Relationships:
- Higher Ea → Slower reaction
- Lower Ea → Faster reaction
- Temperature affects the fraction of molecules with E ≥ Ea
Maxwell-Boltzmann Distribution
The Maxwell-Boltzmann distribution shows how molecular energies are distributed at a given temperature:
Temperature Effects:
- Higher T → More molecules have E ≥ Ea
- Higher T → Faster reaction rates
- Curve shifts to higher energies but maintains same area
Reaction Energy Profiles
Understanding Energy Diagrams
Reaction energy profiles (or reaction coordinate diagrams) show how potential energy changes as reactants transform into products.
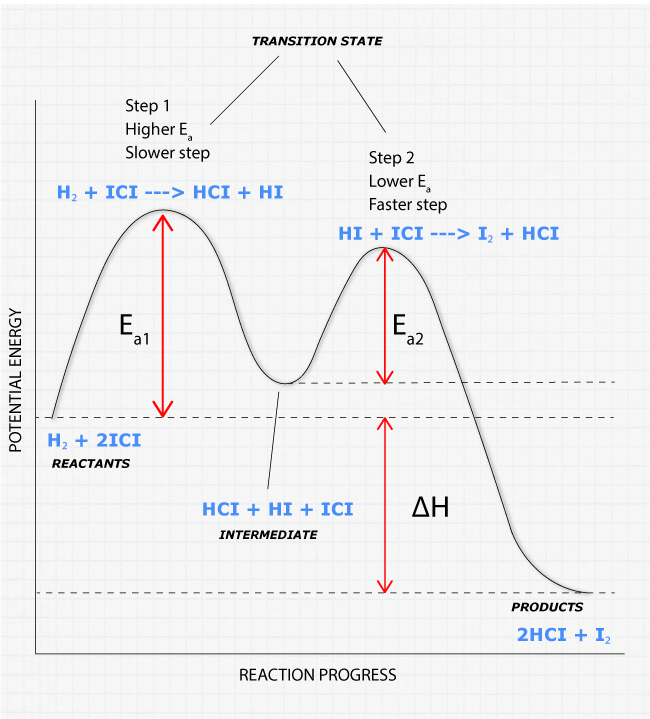
Key Features of Energy Profiles
- Reactants: Starting materials (left side)
- Products: Final materials (right side)
- Transition State: Highest energy point along reaction path
- Activation Energy (Ea): Energy difference between reactants and transition state
- ΔH: Overall energy change (products – reactants)
Exothermic vs Endothermic Reactions
Exothermic Reactions (ΔH < 0):
- Products lower in energy than reactants
- Energy is released
- Generally favorable
Endothermic Reactions (ΔH > 0):
- Products higher in energy than reactants
- Energy must be supplied
- Less favorable thermodynamically
Arrhenius Equation (Qualitative Understanding)
The Arrhenius equation relates rate constant to temperature:
k = Ae^(-Ea/RT)Qualitative Interpretation:
- Higher temperature → Higher k → Faster reaction
- Higher Ea → Lower k → Slower reaction
- A (frequency factor) relates to collision frequency and geometry
Note: Quantitative calculations with the Arrhenius equation are not required on the AP exam, but understanding the relationships is essential.
Reaction Mechanisms
What is a Reaction Mechanism?
A reaction mechanism is a sequence of elementary steps that shows how reactants transform into products at the molecular level.
Example Mechanism:
Step 1 (slow): A + B → I (rate-determining step)
Step 2 (fast): I + C → P
Overall: A + B + C → PComponents of Mechanisms
- Elementary Steps: Individual molecular events
- Intermediates: Species produced in one step and consumed in another
- Rate-Determining Step: Slowest step that controls overall rate
- Catalysts: Species that appear in mechanism but not overall equation
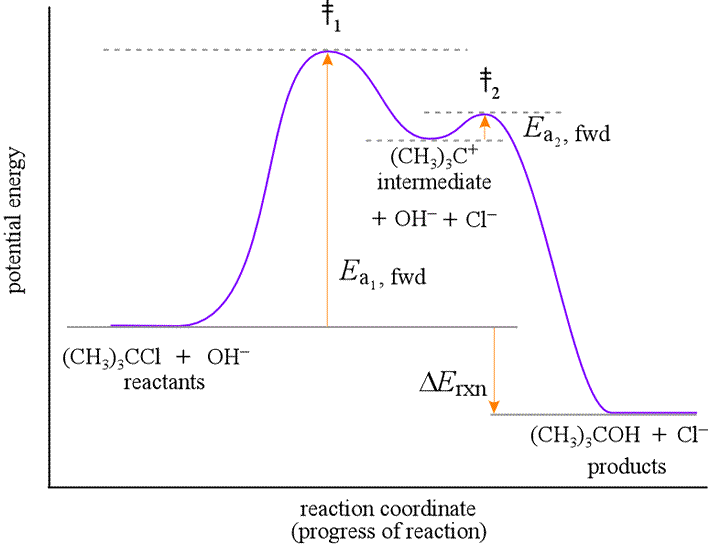
Characteristics of Valid Mechanisms
- Elementary steps must sum to overall reaction
- Rate law derived from mechanism must match experimental rate law
- All intermediates must be consumed
- Mechanism must be chemically reasonable
Rate Laws from Mechanisms
Case 1: First Step is Rate-Determining
Step 1 (slow): A + B → I
Step 2 (fast): I + C → PRate law is determined by slowest step: Rate = k[A][B]
Case 2: First Step Not Rate-Determining (Pre-equilibrium)
Step 1 (fast equilibrium): A ⇌ I
Step 2 (slow): I + B → PMore complex analysis required using pre-equilibrium approximation (details not required for AP exam).
Identifying Intermediates and Catalysts
Intermediates:
- Produced in one step, consumed in another
- Do not appear in overall equation
- Can sometimes be detected experimentally
Catalysts:
- Consumed in one step, regenerated in another
- Appear in both reactants and products of overall equation
- Net concentration unchanged
Catalysis and Activation Energy
How Catalysts Work
Catalysts increase reaction rates by providing alternative pathways with lower activation energy. They do not change the thermodynamics (ΔH) of the reaction.

Types of Catalysts
Homogeneous Catalysts
- Same phase as reactants
- Often involve formation of intermediate complexes
- Example: Acid catalysis in esterification
Mechanism:
Step 1: H⁺ + RCOOH ⇌ RCOOH₂⁺
Step 2: RCOOH₂⁺ + R'OH → RCOOR' + H₂O + H⁺Heterogeneous Catalysts
- Different phase from reactants (usually solid catalyst, gas/liquid reactants)
- Reaction occurs on catalyst surface
- Example: Pt in catalytic converters
Enzyme Catalysis
- Biological catalysts with extreme specificity
- Can increase rates by factors of 10⁶ to 10¹²
- Work by stabilizing transition states
Surface Catalysis Mechanism
Step 1: A(g) + Surface → A-Surface (adsorption)
Step 2: B(g) + Surface → B-Surface (adsorption)
Step 3: A-Surface + B-Surface → AB-Surface (reaction)
Step 4: AB-Surface → AB(g) + Surface (desorption)Key Point: Surface area is crucial – nanoparticles are highly effective due to high surface area to volume ratio.
Problem-Solving Mastery
Strategy for Kinetics Problems
- Identify what’s being asked: Rate law, order, mechanism, etc.
- Organize given data: Make tables for clarity
- Choose appropriate method: Initial rates, graphical, etc.
- Apply mathematical relationships: Use correct equations
- Check units and reasonableness: Ensure answers make sense
Common Problem Types
Type 1: Determining Rate Law from Initial Rates
Example Problem:
For the reaction A + B → C, initial rate data:
Solution:
- Compare experiments 1 & 2: [A] doubles, rate increases 4× → order in A = 2
- Compare experiments 1 & 3: [B] triples, rate unchanged → order in B = 0
- Rate law: Rate = k[A]²
- Calculate k: k = Rate/[A]² = (1.2 × 10⁻³)/(0.10)² = 0.12 M⁻¹s⁻¹
Type 2: Using Integrated Rate Laws
Example Problem:
For a first-order reaction with k = 0.693 s⁻¹, if [A]₀ = 1.0 M, find [A] after 2.0 s.
Solution:
- Use first-order integrated rate law: ln[A] = ln[A]₀ – kt
- Substitute: ln[A] = ln(1.0) – (0.693)(2.0) = 0 – 1.386 = -1.386
- Solve: [A] = e⁻¹·³⁸⁶ = 0.25 M
Type 3: Half-Life Calculations
Example Problem:
A first-order reaction has a half-life of 10.0 minutes. What fraction remains after 30.0 minutes?
Solution:
- Number of half-lives = 30.0/10.0 = 3
- After 3 half-lives: Fraction remaining = (1/2)³ = 1/8 = 0.125
Multiple Choice Practice Questions
Questions 1-10: Rate Laws and Orders
1. For the reaction A + B → C, doubling [A] doubles the rate, while doubling [B] has no effect. The rate law is:
- A) Rate = k[A][B]
- B) Rate = k[A]²[B]
- C) Rate = k[A]
- D) Rate = k[B]
Answer: C – Since doubling [A] doubles the rate, order in A = 1. Since [B] has no effect, order in B = 0.
2. Which plot would be linear for a second-order reaction?
- A) [A] vs t
- B) ln[A] vs t
- C) 1/[A] vs t
- D) [A]² vs t
Answer: C – Second-order integrated rate law: 1/[A] = 1/[A]₀ + kt gives linear plot of 1/[A] vs t.
3. The half-life of a first-order reaction is 20 minutes. The rate constant is:
- A) 0.0347 min⁻¹
- B) 0.693 min⁻¹
- C) 20 min⁻¹
- D) 40 min⁻¹
Answer: A – For first-order: k = 0.693/t₁/₂ = 0.693/20 = 0.0347 min⁻¹
4. At higher temperature, reaction rates increase primarily because:
- A) Molecules move faster
- B) More molecules have sufficient activation energy
- C) Activation energy decreases
- D) Concentration increases
Answer: B – Higher temperature shifts Maxwell-Boltzmann distribution, increasing fraction of molecules with E ≥ Ea.
5. For elementary reaction 2A → Products, the rate law is:
- A) Rate = k[A]
- B) Rate = k[A]²
- C) Rate = k[A]²[Products]
- D) Cannot be determined
Answer: B – For elementary reactions, rate law matches stoichiometry: Rate = k[A]².
6. Which factor does NOT affect reaction rate?
- A) Temperature
- B) Concentration
- C) ΔH of reaction
- D) Presence of catalyst
Answer: C – ΔH (enthalpy change) affects thermodynamics but not kinetics. Rate depends on activation energy, not overall energy change.
7. A catalyst increases reaction rate by:
- A) Increasing collision frequency
- B) Lowering activation energy
- C) Changing the equilibrium position
- D) Increasing reactant concentration
Answer: B – Catalysts provide alternative pathways with lower Ea, allowing more molecules to react.
8. For reaction A → B, if ln[A] vs t gives slope = -0.25 s⁻¹, the reaction is:
- A) Zero order, k = 0.25 s⁻¹
- B) First order, k = 0.25 s⁻¹
- C) Second order, k = 0.25 s⁻¹
- D) Cannot determine order
Answer: B – Linear ln[A] vs t indicates first-order with slope = -k, so k = 0.25 s⁻¹.
9. In a mechanism, an intermediate:
- A) Appears in the overall equation
- B) Is consumed in one step and produced in another
- C) Is produced in one step and consumed in another
- D) Catalyzes the reaction
Answer: C – Intermediates are produced in early steps and consumed in later steps.
10. The rate-determining step in a mechanism is:
- A) The first step
- B) The last step
- C) The slowest step
- D) The step with highest activation energy
Answer: C – The slowest step controls the overall reaction rate.
Questions 11-20: Advanced Concepts
11. For the mechanism:
Step 1: A ⇌ B (fast equilibrium)
Step 2: B + C → D (slow)
The rate law is:
- A) Rate = k[A][C]
- B) Rate = k[B][C]
- C) Rate = k[A]²[C]
- D) Cannot be determined without equilibrium constant
Answer: A – Using pre-equilibrium approximation, [B] ∝ [A], so Rate = k'[A][C].
12. If activation energy increases, the rate constant:
- A) Increases
- B) Decreases
- C) Stays the same
- D) Depends on temperature
Answer: B – From Arrhenius equation, higher Ea leads to smaller k.
13. A reaction has rate law Rate = k[A]²[B]. If [A] triples and [B] doubles, the rate:
- A) Increases 6×
- B) Increases 12×
- C) Increases 18×
- D) Increases 36×
Answer: C – Rate factor = (3)² × (2) = 9 × 2 = 18×
14. Which statement about catalysts is FALSE?
- A) They lower activation energy
- B) They are regenerated in the reaction
- C) They change the reaction mechanism
- D) They change the equilibrium constant
Answer: D – Catalysts affect kinetics but not thermodynamic equilibrium.
15. For radioactive decay following first-order kinetics, after 3 half-lives:
- A) 12.5% remains
- B) 25% remains
- C) 33% remains
- D) 50% remains
Answer: A – After n half-lives: fraction = (1/2)ⁿ = (1/2)³ = 1/8 = 12.5%
16. The units of the rate constant for a third-order reaction are:
- A) s⁻¹
- B) M⁻¹s⁻¹
- C) M⁻²s⁻¹
- D) M²s⁻¹
Answer: C – For nth order: units = M¹⁻ⁿs⁻¹ = M¹⁻³s⁻¹ = M⁻²s⁻¹
17. In collision theory, increasing temperature increases rate because:
- A) Molecules collide more frequently
- B) Molecules have better orientation
- C) More collisions have sufficient energy
- D) Activation energy decreases
Answer: C – Higher T increases fraction of molecules with E ≥ Ea.
18. Which reaction coordinate diagram shows the effect of a catalyst?
[This would show two curves – one higher (uncatalyzed) and one lower (catalyzed) with same start/end points]
Answer: The diagram showing lower activation energy with unchanged ΔH
19. For elementary reaction A + 2B → Products:
- A) Rate = k[A][B]
- B) Rate = k[A][B]²
- C) Rate = k[A]²[B]²
- D) Rate law cannot be predicted
Answer: B – Elementary rate law matches stoichiometry: Rate = k[A][B]²
20. A second-order reaction has k = 0.10 M⁻¹s⁻¹. If [A]₀ = 1.0 M, the half-life is:
- A) 5.0 s
- B) 6.9 s
- C) 10 s
- D) 20 s
Answer: C – For second-order: t₁/₂ = 1/(k[A]₀) = 1/(0.10 × 1.0) = 10 s
Free Response Problems
Problem 1: Rate Law Determination (15 points)
The decomposition of hydrogen peroxide in aqueous solution follows the reaction:
2 H₂O₂(aq) → 2 H₂O(l) + O₂(g)The following initial rate data were collected at 298 K:
| Experiment | H₂O₂ | I⁻ | Initial Rate (M/s) |
|---|---|---|---|
| 1 | 0.10 | 0.010 | 1.8 × 10⁻⁵ |
| 2 | 0.20 | 0.010 | 3.6 × 10⁻⁵ |
| 3 | 0.10 | 0.020 | 3.6 × 10⁻⁵ |
| 4 | 0.30 | 0.030 | 1.6 × 10⁻⁴ |
Note: I⁻ acts as a catalyst
(a) Determine the rate law for this reaction. Show your work. (4 points)
(b) Calculate the rate constant and specify its units. (3 points)
(c) Predict the initial rate when [H₂O₂] = 0.25 M and [I⁻] = 0.015 M. (2 points)
(d) Explain why I⁻ appears in the rate law even though it’s not in the balanced equation. (3 points)
(e) Sketch a reaction energy diagram showing the catalyzed and uncatalyzed pathways. Label activation energies and explain how the catalyst affects the reaction. (3 points)
Solution:
(a) Determining Rate Law (4 points)
Assume rate law: Rate = k[H₂O₂]^m[I⁻]^n
Finding order in H₂O₂ (m):
Compare experiments 1 and 2 (constant [I⁻]):
- [H₂O₂] ratio: 0.20/0.10 = 2
- Rate ratio: (3.6 × 10⁻⁵)/(1.8 × 10⁻⁵) = 2
- 2^m = 2, therefore m = 1
Finding order in I⁻ (n):
Compare experiments 1 and 3 (constant [H₂O₂]):
- [I⁻] ratio: 0.020/0.010 = 2
- Rate ratio: (3.6 × 10⁻⁵)/(1.8 × 10⁻⁵) = 2
- 2^n = 2, therefore n = 1
Rate law: Rate = k[H₂O₂][I⁻]
(b) Rate Constant Calculation (3 points)
Using experiment 1:
1.8 × 10⁻⁵ = k(0.10)(0.010)
k = (1.8 × 10⁻⁵)/(1.0 × 10⁻³) = 1.8 × 10⁻² M⁻¹s⁻¹Verification with experiment 4:
Rate = (1.8 × 10⁻²)(0.30)(0.030) = 1.6 × 10⁻⁴ M/s ✓k = 1.8 × 10⁻² M⁻¹s⁻¹
(c) Rate Prediction (2 points)
Rate = k[H₂O₂][I⁻]
Rate = (1.8 × 10⁻²)(0.25)(0.015) = 6.8 × 10⁻⁵ M/s(d) Catalyst Explanation (3 points)
I⁻ appears in the rate law because it participates in the reaction mechanism as a catalyst. Although catalysts are not consumed overall, they:
- React with H₂O₂ in the rate-determining step
- Are regenerated in a subsequent fast step
- Provide an alternative pathway with lower activation energy
- Their concentration affects the rate of the slow step
(e) Energy Diagram (3 points)
[Diagram would show two curves with same reactant/product levels but different activation barriers, with the catalyzed path having lower Ea]
The catalyst lowers the activation energy by providing an alternative mechanism. The overall energy change (ΔH) remains the same, but more molecules have sufficient energy to react via the catalyzed pathway.
Problem 2: Integrated Rate Laws (12 points)
The thermal decomposition of SO₂Cl₂ follows first-order kinetics:
SO₂Cl₂(g) → SO₂(g) + Cl₂(g)At 593 K, the following data were collected:
| Time (s) | SO₂Cl₂ |
|---|---|
| 0 | 0.200 |
| 100 | 0.162 |
| 200 | 0.131 |
| 300 | 0.106 |
| 400 | 0.086 |
(a) Verify that this reaction follows first-order kinetics by plotting the appropriate graph. (3 points)
(b) Determine the rate constant from your graph. (2 points)
(c) Calculate the half-life of this reaction. (2 points)
(d) Predict the concentration after 600 seconds. (2 points)
(e) How long will it take for 90% of the SO₂Cl₂ to decompose? (3 points)
Solution:
(a) First-Order Verification (3 points)
For first-order kinetics, plot ln[SO₂Cl₂] vs time should be linear.
| Time (s) | SO₂Cl₂ | ln[SO₂Cl₂] |
|---|---|---|
| 0 | 0.200 | -1.609 |
| 100 | 0.162 | -1.820 |
| 200 | 0.131 | -2.032 |
| 300 | 0.106 | -2.244 |
| 400 | 0.086 | -2.453 |
The plot is linear, confirming first-order kinetics.
(b) Rate Constant (2 points)
From the slope of ln[A] vs t:
slope = Δ(ln[SO₂Cl₂])/Δt = (-2.453 – (-1.609))/(400 – 0) = -0.844/400 = -2.11 × 10⁻³ s⁻¹
Since slope = -k: k = 2.11 × 10⁻³ s⁻¹
(c) Half-Life (2 points)
For first-order reactions:
t₁/₂ = 0.693/k = 0.693/(2.11 × 10⁻³) = 328 s(d) Concentration at 600 s (2 points)
Using ln[A] = ln[A]₀ – kt:
ln[SO₂Cl₂] = ln(0.200) - (2.11 × 10⁻³)(600)
ln[SO₂Cl₂] = -1.609 - 1.266 = -2.875
[SO₂Cl₂] = e⁻²·⁸⁷⁵ = 0.056 M(e) Time for 90% Decomposition (3 points)
90% decomposition means 10% remains: [A] = 0.10[A]₀ = 0.020 M
ln(0.020) = ln(0.200) - (2.11 × 10⁻³)t
-3.912 = -1.609 - (2.11 × 10⁻³)t
-2.303 = -(2.11 × 10⁻³)t
t = 1091 sProblem 3: Reaction Mechanisms (10 points)
Consider the following proposed mechanism for the reaction:
Overall: 2 A + B → C + DMechanism:
Step 1: A + B ⇌ I (fast equilibrium)
Step 2: A + I → C + D (slow)(a) Identify any intermediates in this mechanism. (1 point)
(b) Derive the rate law for the overall reaction using the pre-equilibrium approximation. (4 points)
(c) If the experimental rate law is Rate = k[A]²[B], is this mechanism consistent? Explain. (2 points)
(d) Sketch a reaction energy diagram for this two-step mechanism, labeling all species and energy barriers. (3 points)
Solution:
(a) Intermediates (1 point)
I is the only intermediate (produced in step 1, consumed in step 2).
(b) Rate Law Derivation (4 points)
Since step 2 is slow (rate-determining):
Rate = k₂[A][I]
For fast pre-equilibrium in step 1:
K₁ = [I]/([A][B])
Therefore: [I] = K₁[A][B]Substituting into rate expression:
Rate = k₂[A](K₁[A][B]) = k₂K₁[A]²[B]Overall rate law: Rate = k'[A]²[B] where k’ = k₂K₁
(c) Mechanism Consistency (2 points)
Yes, the mechanism is consistent. The derived rate law (Rate = k'[A]²[B]) matches the experimental rate law (Rate = k[A]²[B]). The observed rate constant k equals k₂K₁.
(d) Energy Diagram (3 points)
[Diagram would show: Reactants (2A + B) → Transition State 1 → Intermediate (A + I) → Transition State 2 (higher) → Products (C + D)]
The diagram shows two activation barriers, with the second being higher (rate-determining step).
Study Strategies and Exam Tips
Effective Study Techniques
1. Master the Mathematics
- Practice rate law calculations daily
- Memorize integrated rate law forms
- Work with logarithms and exponentials
- Use dimensional analysis for unit consistency
2. Visual Learning Strategies
- Create reaction energy diagrams
- Draw concentration vs. time graphs
- Use molecular models for collision theory
- Sketch mechanisms step-by-step
3. Conceptual Understanding
- Connect kinetics to everyday examples
- Explain why catalysts work
- Relate temperature effects to molecular behavior
- Understand difference between thermodynamics and kinetics
Memory Techniques
Rate Law Acronyms
“King Carl Ate Many Nachos” = k, concentration, activation, molecular, nature (factors affecting rate)
Graph Recognition
- Zero order: Zero slope decline (linear [A] vs t)
- First order: Falling exponentially (linear ln[A] vs t)
- Second order: Steep curve (linear 1/[A] vs t)
Half-Life Memory
- First-order: t₁/₂ = 0.693/k (constant)
- Zero-order: t₁/₂ = [A]₀/2k (depends on concentration)
- Second-order: t₁/₂ = 1/k[A]₀ (depends on concentration)
Time Management for Exam Day
Multiple Choice Strategy (90 minutes, 60 questions)
- 1.5 minutes per question maximum
- Skip difficult calculations initially
- Return to computational problems after easier questions
- Use process of elimination
Free Response Strategy (105 minutes, 7 questions)
- 15 minutes per question average
- Read all questions first
- Start with strongest topics
- Show all work clearly
- Use proper significant figures
Common Error Prevention
Mathematical Errors
- Check units consistently
- Use correct logarithm properties
- Apply stoichiometry properly in rate expressions
- Avoid mixing up ln and log₁₀
- Don’t forget negative signs in integrated rate laws
Conceptual Errors
- Distinguish elementary vs. overall reactions
- Identify intermediates vs. catalysts correctly
- Remember catalysts don’t change ΔH
- Don’t confuse reaction order with stoichiometry
- Don’t assume rate laws from balanced equations
Real-World Applications
Industrial Chemistry
Catalytic Processes
Haber Process (NH₃ production):
N₂ + 3H₂ ⇌ 2NH₃- Uses Fe catalyst to lower activation energy
- Temperature optimization balances rate vs. equilibrium
- Feeds global food production through fertilizers
Catalytic Converters:
2CO + 2NO → 2CO₂ + N₂- Pt/Pd/Rh catalysts enable rapid conversion
- Surface area maximized through honeycomb structure
- Reduces automotive emissions significantly
Pharmaceutical Industry
Drug Development:
- Reaction kinetics determine synthesis efficiency
- Catalyst selection affects production costs
- Understanding mechanisms enables drug design
Drug Metabolism:
- Most drugs follow first-order elimination kinetics
- Half-life determines dosing intervals
- Enzyme kinetics govern drug effectiveness
Environmental Science
Atmospheric Chemistry
Ozone Depletion:
Cl + O₃ → ClO + O₂ (fast)
ClO + O → Cl + O₂ (regeneration)- Cl acts as catalyst, destroying thousands of O₃ molecules
- Understanding mechanisms led to CFC ban
- Kinetic studies predict atmospheric recovery times
Greenhouse Gas Reactions:
- CH₄ oxidation rates affect global warming potential
- CO₂ dissolution kinetics impact ocean acidification
- Reaction rates determine atmospheric lifetimes
Pollution Remediation
Groundwater Treatment:
- Zero-order kinetics in saturated enzyme systems
- First-order kinetics for natural biodegradation
- Rate constants determine cleanup timeframes
Food Science
Food Preservation
Arrhenius Applications:
- Temperature reduction slows spoilage reactions
- Q₁₀ rule: 10°C decrease often halves reaction rate
- Kinetic studies optimize storage conditions
Enzymatic Browning:
Phenol + O₂ → Quinone → Brown polymers- Understanding mechanism enables prevention strategies
- Antioxidants act as inhibitors
- pH affects enzyme kinetics
Materials Science
Polymer Chemistry
Polymerization Kinetics:
- Chain growth follows complex kinetic schemes
- Catalyst choice affects polymer properties
- Rate constants determine molecular weight distributions
Degradation Studies:
- UV degradation follows first-order kinetics
- Activation energy predicts material lifetimes
- Stabilizers act as reaction inhibitors
FAQs and Common Mistakes
Frequently Asked Questions
Q1: How do I know if a reaction is elementary?
A: Elementary reactions are explicitly stated as single-step processes. For multi-step overall reactions, rate laws must be determined experimentally. Elementary reactions are rare except for simple processes like radioactive decay.
Q2: Why can’t I determine rate law from balanced equations?
A: Balanced equations show overall stoichiometry but not mechanism. Rate laws reflect the actual pathway (mechanism) which may involve multiple steps. Only elementary reactions have rate laws matching stoichiometry.
Q3: What’s the difference between reaction order and molecularity?
A:
- Order: Experimental quantity (can be fractional, negative, or zero)
- Molecularity: Number of molecules in elementary step (always positive integer)
Q4: How do catalysts appear in mechanisms?
A: Catalysts are consumed in early steps and regenerated in later steps. They appear in intermediate steps but cancel out in the overall equation. Their concentration affects the rate law.
Q5: Why is the Arrhenius equation not required for calculations?
A: The AP exam focuses on qualitative understanding of temperature-rate relationships. You should understand that higher temperature and lower activation energy increase rates, but quantitative Arrhenius calculations are beyond the scope.
Q6: How do I identify the rate-determining step?
A: The rate-determining step is explicitly stated as “slow” in mechanisms. It controls the overall rate and determines the rate law for simple mechanisms where it’s the first step.
Q7: What makes a good catalyst?
A: Effective catalysts:
- Lower activation energy significantly
- Are chemically stable under reaction conditions
- Have high surface area (for heterogeneous catalysis)
- Are selective for desired products
- Are economically feasible
Common Mistakes and How to Avoid Them
Mistake 1: Confusing Rate and Rate Law
Wrong: “The rate is k[A]²”
Correct: “The rate law is Rate = k[A]², and the rate at this moment is…”
Fix: Always specify units and distinguish between the expression (rate law) and the calculated value (rate).
Mistake 2: Using Stoichiometry for Rate Laws
Wrong: For 2A + B → C, assuming Rate = k[A]²[B]
Correct: Rate law must be determined experimentally
Fix: Remember that balanced equations don’t reveal mechanisms. Only use stoichiometry for elementary reactions.
Mistake 3: Incorrect Graph Identification
Wrong: Thinking any decreasing curve is first-order
Correct: Recognizing specific linear relationships
Fix: Practice plotting all three forms (concentration, ln, and reciprocal) and memorize which gives straight lines for each order.
Mistake 4: Half-Life Confusion
Wrong: Using t₁/₂ = 0.693/k for all reactions
Correct: This only applies to first-order reactions
Fix: Memorize that only first-order half-lives are concentration-independent.
Mistake 5: Catalyst Misconceptions
Wrong: “Catalysts change equilibrium position”
Correct: “Catalysts change the pathway but not thermodynamics”
Fix: Remember catalysts affect kinetics only – they change how fast equilibrium is reached, not where it lies.
Mistake 6: Intermediate vs. Product Confusion
Wrong: Calling products “intermediates”
Correct: Intermediates are consumed during the reaction
Fix: Intermediates appear and disappear within the mechanism – they’re temporary species.
Mistake 7: Unit Analysis Errors
Wrong: Getting rate constants with incorrect units
Correct: Units must be consistent with M^(1-n)s^(-1)
Fix: Always check that units work out properly in rate equations.
Conclusion and Next Steps
Mastery Summary
Congratulations on completing this comprehensive guide to AP Chemistry Unit 5: Kinetics! You’ve now developed a thorough understanding of:
✅ Rate laws and reaction orders – How to determine and use them
✅ Integrated rate laws – Mathematical relationships connecting concentration and time
✅ Collision theory – Molecular-level understanding of reaction rates
✅ Energy profiles – Visual representation of reaction pathways
✅ Reaction mechanisms – Step-by-step molecular processes
✅ Catalysis – How catalysts accelerate reactions without being consumed
✅ Problem-solving strategies – Systematic approaches to kinetics problems
Key Takeaways for AP Success
- Kinetics is about “how fast” not “how far” – Don’t confuse with thermodynamics
- Rate laws come from experiments, not balanced equations – Except for elementary reactions
- Graphs are your friends – Linear relationships reveal reaction orders
- Mechanisms tell the real story – Overall equations hide the molecular details
- Temperature and catalysts are rate game-changers – Understand their molecular effects
Connecting to Other Units
Unit 5 Kinetics connects strongly to:
- Unit 4 (Chemical Reactions): Provides the reactions that kinetics studies
- Unit 6 (Thermochemistry): Energy changes related to activation energy
- Unit 7 (Equilibrium): Rate concepts help understand equilibrium achievement
- Unit 8 (Acids and Bases): Catalysis by H⁺ and OH⁻ ions
- Unit 9 (Applications): Real-world kinetic applications
Next Steps for Continued Learning
Immediate Actions
- Complete practice exams focusing on kinetics problems
- Review and rework any problems you found challenging
- Create summary cards with key formulas and concepts
- Form study groups to discuss mechanisms and energy diagrams
Advanced Study (For Future Chemistry Courses)
- Enzyme kinetics – Michaelis-Menten equations
- Complex reaction mechanisms – Pre-equilibrium and steady-state approximations
- Advanced catalysis – Homogeneous and heterogeneous catalyst design
- Computational chemistry – Modeling reaction pathways and transition states
Resources for Continued Practice
College Board Resources:
- AP Chemistry Course and Exam Description
- AP Classroom practice problems
- Previous AP exam questions with scoring guidelines
Additional Practice:
- Khan Academy AP Chemistry Unit 5
- ChemTalk kinetics problems
- University general chemistry textbooks
Experimental Connections:
- Try simple rate experiments at home (catalase with hydrogen peroxide)
- Observe temperature effects on reaction rates
- Research industrial catalytic processes
Final Motivation
Chemical kinetics is one of the most practically relevant topics in chemistry. From the food you eat to the medicines that heal you, from the catalytic converters in cars to the enzymes in your body – kinetics is everywhere. The concepts you’ve mastered here aren’t just for passing an exam; they’re tools for understanding and improving the world around you.
Every great chemist, from Nobel Prize winners to industrial researchers, has used these same fundamental principles to:
- Design life-saving drugs
- Develop clean energy technologies
- Create new materials with amazing properties
- Solve environmental challenges
You now possess these same powerful tools. Whether you pursue chemistry professionally or apply these concepts in other fields, you have the foundation to understand and predict how reactions behave – a skill that will serve you well in any scientific endeavor.
Success Strategies for Test Day
The Night Before:
- Light review of key formulas
- Get adequate sleep (your brain needs rest!)
- Prepare materials and documents
- Stay positive and confident
Test Day Morning:
- Eat a good breakfast
- Arrive early but not too early
- Bring backup calculators and pencils
- Trust your preparation
During the Exam:
- Read questions carefully
- Manage your time wisely
- Show all work clearly
- Don’t panic if something seems unfamiliar
Remember: You’ve put in the work, understood the concepts, and practiced extensively. Trust in your preparation and let your knowledge shine through!
Good luck with your AP Chemistry exam, and remember – kinetics is the key to understanding how our chemical world actually works!
This comprehensive guide covers all essential concepts in AP Chemistry Unit 5: Kinetics. For personalized help and additional practice problems, consider working with a qualified AP Chemistry tutor or joining a Solvefy AI . Remember, mastering kinetics opens doors to understanding countless chemical processes that shape our world every day.
Also Read –


2 thoughts on “AP Chemistry Unit 5: Kinetics – Complete Mastery Guide for Chemical Reaction Rates”