Picture this: You’re watching your favorite NFL running back burst through the defensive line, carrying 250-pound linebackers on his back as he powers toward the end zone. What makes this incredible display of physics possible? The answer lies in one of the most fundamental concepts in physics – linear momentum. Whether it’s a quarterback throwing a perfect spiral, a car crash that triggers airbags in milliseconds, or a rocket launching into space, momentum governs the motion of everything around us.
Welcome to your comprehensive guide to AP Physics 1 Unit 4: Linear Momentum. This unit builds beautifully on everything you’ve learned about forces and Newton’s laws, transforming those concepts into powerful conservation principles that help us understand collisions, explosions, and the fundamental nature of motion itself.
Learning Objectives: What You’ll Master by the End
By the time you complete this unit, you’ll have developed a deep understanding of momentum that goes far beyond memorizing formulas. You’ll be able to:
- Conceptually understand momentum as both a vector quantity and a measure of an object’s “quantity of motion”
- Apply the impulse-momentum theorem to analyze how forces change an object’s momentum over time
- Master conservation of momentum in both one and two-dimensional collision scenarios
- Distinguish between elastic and inelastic collisions and predict their outcomes
- Solve complex multi-object systems using momentum conservation principles
- Connect momentum concepts to real-world applications from automotive safety to space exploration
- Approach AP exam problems with confidence using systematic problem-solving strategies
This unit typically represents 10-15% of the AP Physics 1 exam, making it a high-yield topic that deserves your focused attention. More importantly, momentum concepts provide the foundation for understanding energy conservation and rotational motion in later units.
Understanding Linear Momentum: More Than Just “Mass Times Velocity”
Let’s start with the fundamental question: What exactly is momentum? While the mathematical definition is straightforward (p = mv), the conceptual understanding runs much deeper.
Physics Check: Momentum is a vector quantity that measures an object’s “quantity of motion” – combining both how much stuff is moving (mass) and how fast it’s moving (velocity).
Think about momentum this way: imagine you’re standing on ice wearing roller skates. If a tennis ball flying at 30 m/s hits you, you’ll barely budge. But if a bowling ball moving at just 3 m/s hits you, you’ll go sliding across the ice. The bowling ball has much more momentum because its greater mass more than compensates for its slower speed.
The Vector Nature of Momentum
Unlike speed or kinetic energy, momentum has both magnitude and direction. This vector property becomes crucial when analyzing collisions and explosions in two dimensions. The momentum vector always points in the same direction as the velocity vector, but its magnitude depends on both mass and speed.
For an object with mass m moving with velocity v, the momentum p is:
p = mv
The SI unit for momentum is kg⋅m/s, though you’ll sometimes see it written as N⋅s (Newton-seconds), which comes from the impulse-momentum theorem we’ll explore shortly.
Real-World Physics: Why do large trucks have much longer stopping distances than cars? Even when traveling at the same speed, a fully loaded semi-truck has roughly 20 times more momentum than a typical car due to its massive mass. This enormous momentum requires much larger forces or much longer times to change – hence the extended stopping distances and runaway truck ramps on steep mountain highways.
Momentum in One Dimension vs. Two Dimensions
In one-dimensional problems, momentum calculations are relatively straightforward since we only need to worry about positive and negative directions. However, real-world collisions often occur in two or three dimensions, requiring vector addition and trigonometry.
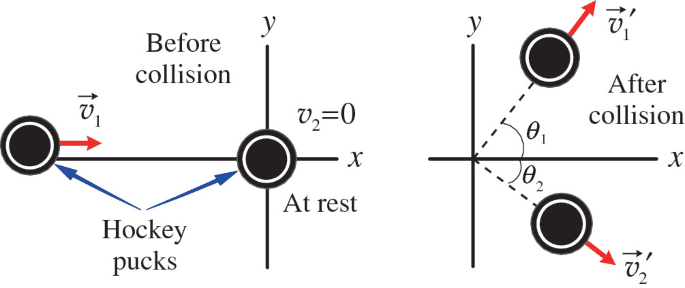
Consider a hockey puck sliding across ice. Its momentum vector points exactly in its direction of travel. But when it collides with another puck at an angle, both pucks’ momentum vectors change direction and magnitude, creating a two-dimensional momentum conservation problem.
The Impulse-Momentum Theorem: Connecting Force and Time
One of the most elegant relationships in physics connects the concepts of force, time, and momentum through the impulse-momentum theorem. This principle explains everything from why airbags save lives to how rocket engines propel spacecraft through the vacuum of space.
Deriving the Impulse-Momentum Theorem
Starting with Newton’s second law in its most fundamental form:
F = dp/dt
Rearranging and integrating over time:
∫F dt = Δp = p_final – p_initial
The left side of this equation (∫F dt) is called impulse, represented by the symbol J. The impulse-momentum theorem states:
J = Δp
In words: The impulse delivered to an object equals the change in that object’s momentum.
Understanding Impulse Graphically
When force remains constant over time interval Δt, impulse simply equals F⋅Δt. But when force varies with time, impulse equals the area under the force-versus-time graph.
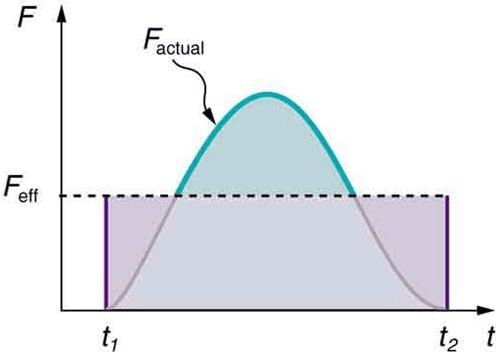
This graphical interpretation helps explain many real-world phenomena. For example, during a car crash, the force between car and barrier isn’t constant – it starts small, builds to a maximum, then decreases as the car crumples and comes to rest.
Applications of the Impulse-Momentum Theorem
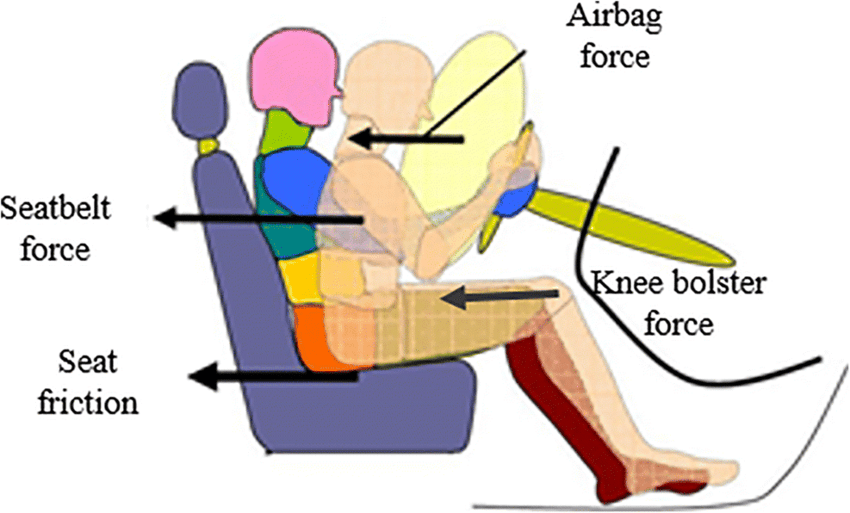
Automotive Safety Systems
Modern cars incorporate numerous safety features based on impulse-momentum principles. Airbags, crumple zones, and seat belts all work by extending the collision time, thereby reducing the force experienced by passengers.
Consider a 70-kg passenger traveling at 25 m/s (about 56 mph) who must come to a complete stop during a collision:
- Initial momentum: p = (70 kg)(25 m/s) = 1,750 kg⋅m/s
- Final momentum: p = 0 kg⋅m/s
- Change in momentum: Δp = -1,750 kg⋅m/s
Without safety systems, this passenger might stop in just 0.1 seconds, requiring an average force of:
F = Δp/Δt = 1,750 kg⋅m/s ÷ 0.1 s = 17,500 N
That’s equivalent to about 2.5 times the person’s weight – likely fatal.
With airbags and crumple zones extending the collision time to 0.5 seconds:
F = 1,750 kg⋅m/s ÷ 0.5 s = 3,500 N
While still significant, this reduced force is much more survivable.
Common Physics Mistake Alert: Students often confuse impulse with impact. Remember that impulse depends on both force AND time. A small force acting for a long time can produce the same impulse as a large force acting for a short time.
Conservation of Momentum: The Universal Principle
The law of conservation of momentum stands as one of physics’ most fundamental principles. Unlike energy, which can change forms, the total momentum of an isolated system remains absolutely constant, regardless of what happens within that system.
The Theoretical Foundation
Conservation of momentum emerges directly from Newton’s third law. When two objects interact, they exert equal and opposite forces on each other. By the impulse-momentum theorem, these forces create equal and opposite changes in momentum, keeping the total momentum constant.
For a system of objects with no external forces:
p_total_initial = p_total_final
Σm_iv_i_initial = Σm_iv_i_final
This principle holds true whether we’re analyzing atomic particles in a collider or galaxies moving through space.
Problem-Solving Strategy for Momentum Conservation
- Define your system: Identify all objects whose momentum you need to consider
- Check for external forces: Ensure the system is isolated or external forces are negligible
- Choose coordinate system: Pick directions that simplify your calculations
- Write conservation equations: Set initial total momentum equal to final total momentum
- Solve systematically: Use algebra to find unknowns, checking units and reasonableness
Physics Check: A system has conserved momentum if the net external force is zero. Internal forces between objects in the system don’t affect total momentum – they only redistribute it among the objects.
One-Dimensional Momentum Conservation Examples
Let’s work through a classic collision problem step by step.
Example Problem 1: A 1,200-kg car traveling east at 20 m/s collides head-on with a 1,500-kg truck traveling west at 15 m/s. After the collision, the vehicles stick together. Find their velocity immediately after impact.
Solution:
- Define system: car + truck (isolated during collision)
- Choose coordinates: east = positive direction
- Initial momentum:
- Car: p₁ = (1,200 kg)(+20 m/s) = +24,000 kg⋅m/s
- Truck: p₂ = (1,500 kg)(-15 m/s) = -22,500 kg⋅m/s
- Total: p_initial = 24,000 – 22,500 = +1,500 kg⋅m/s
- Final momentum:
- Combined mass: m_total = 1,200 + 1,500 = 2,700 kg
- p_final = (2,700 kg)(v_final)
- Conservation equation:
1,500 kg⋅m/s = (2,700 kg)(v_final)
v_final = +0.56 m/s (eastward)
Two-Dimensional Momentum Conservation
Real-world collisions often involve objects moving at angles to each other. In these cases, we must apply momentum conservation separately to each coordinate direction.
Example Problem 2: A 0.5-kg ball moving north at 8 m/s collides with a 0.3-kg ball moving east at 10 m/s. After collision, the first ball moves at 6 m/s at 30° east of north. Find the velocity of the second ball after collision.

Solution:
Using coordinate system where north = +y, east = +x:
Initial momentum components:
- Ball 1: p₁ₓ = 0, p₁ᵧ = (0.5)(8) = 4.0 kg⋅m/s
- Ball 2: p₂ₓ = (0.3)(10) = 3.0 kg⋅m/s, p₂ᵧ = 0
- Total: pₓ = 3.0 kg⋅m/s, pᵧ = 4.0 kg⋅m/s
Final momentum of ball 1:
- p₁ₓ’ = (0.5)(6)sin(30°) = 1.5 kg⋅m/s
- p₁ᵧ’ = (0.5)(6)cos(30°) = 2.6 kg⋅m/s
Conservation equations:
- x-direction: 3.0 = 1.5 + (0.3)v₂ₓ’ → v₂ₓ’ = 5.0 m/s
- y-direction: 4.0 = 2.6 + (0.3)v₂ᵧ’ → v₂ᵧ’ = 4.7 m/s
Final velocity of ball 2:
- Magnitude: v₂’ = √[(5.0)² + (4.7)²] = 6.9 m/s
- Direction: θ = tan⁻¹(4.7/5.0) = 43° north of east
Elastic vs. Inelastic Collisions: Energy and Momentum Together
While momentum is always conserved in collisions (assuming no external forces), the same isn’t true for kinetic energy. This distinction leads us to classify collisions into different categories based on what happens to the system’s kinetic energy.
Perfectly Elastic Collisions
In a perfectly elastic collision, both momentum and kinetic energy are conserved. These collisions are somewhat rare in everyday life but provide excellent theoretical examples and occur frequently at the atomic level.
For two objects in a one-dimensional elastic collision:
- Momentum conservation: m₁v₁ᵢ + m₂v₂ᵢ = m₁v₁f + m₂v₂f
- Energy conservation: ½m₁v₁ᵢ² + ½m₂v₂ᵢ² = ½m₁v₁f² + ½m₂v₂f²
Real-World Physics: While no macroscopic collisions are perfectly elastic, some come very close. Steel ball bearings bouncing off each other can have coefficients of restitution near 0.95, meaning they retain 95% of their kinetic energy. Pool balls, properly struck, can achieve coefficients around 0.85-0.95.
Perfectly Inelastic Collisions
At the opposite extreme, perfectly inelastic collisions occur when the colliding objects stick together after impact. These collisions conserve momentum but lose the maximum possible kinetic energy while still satisfying momentum conservation.
The classic example is our earlier car-truck collision where both vehicles remained together after impact. Let’s calculate how much kinetic energy was lost:
Initial kinetic energy:
- Car: KE₁ = ½(1,200)(20)² = 240,000 J
- Truck: KE₂ = ½(1,500)(15)² = 168,750 J
- Total: KE_initial = 408,750 J
Final kinetic energy:
- Combined: KE_final = ½(2,700)(0.56)² = 424 J
Energy lost: 408,750 – 424 = 408,326 J (over 99% of the initial kinetic energy!)
This enormous energy loss explains why car crashes are so destructive – most of the vehicles’ kinetic energy converts to deformation, heat, and sound.
Partially Elastic Collisions
Most real-world collisions fall between perfectly elastic and perfectly inelastic. We characterize these using the coefficient of restitution (e):
e = -(v₁f – v₂f)/(v₁ᵢ – v₂ᵢ)
Where:
- e = 1: perfectly elastic collision
- e = 0: perfectly inelastic collision
- 0 < e < 1: partially elastic collision
Quick Calculation Box:
For a ball dropped from height h that bounces to height h’, the coefficient of restitution is e = √(h’/h). A basketball that bounces to 80% of its drop height has e = √(0.80) = 0.89.
Advanced Problem-Solving Techniques
As you encounter more complex momentum problems on the AP exam, certain strategies will help you approach them systematically and avoid common pitfalls.
Multi-Step Collision Problems
Some problems involve a series of collisions or interactions. The key is treating each collision separately while tracking momentum throughout the entire sequence.
Example Problem 3: A 0.2-kg ball moving at 10 m/s strikes a 0.5-kg ball at rest. After the collision, the first ball rebounds at 2 m/s in the opposite direction. The second ball then collides with a 0.3-kg ball at rest and sticks to it. Find the final velocity of the combined second and third balls.
Solution:
Step 1: First collision (balls 1 and 2)
- Initial: p = (0.2)(10) + (0.5)(0) = 2.0 kg⋅m/s
- Final: p = (0.2)(-2) + (0.5)(v₂)
- Conservation: 2.0 = -0.4 + 0.5v₂ → v₂ = 4.8 m/s
Step 2: Second collision (balls 2 and 3)
- Initial: p = (0.5)(4.8) + (0.3)(0) = 2.4 kg⋅m/s
- Final: p = (0.5 + 0.3)(v_final) = 0.8v_final
- Conservation: 2.4 = 0.8v_final → v_final = 3.0 m/s
Center of Mass and System Analysis
For complex systems, the center of mass concept provides powerful insights. The center of mass of an isolated system moves with constant velocity, regardless of internal interactions.
The center of mass position is:
x_cm = (m₁x₁ + m₂x₂ + … + mₙxₙ)/(m₁ + m₂ + … + mₙ)
And its velocity:
v_cm = (m₁v₁ + m₂v₂ + … + mₙvₙ)/(m₁ + m₂ + … + mₙ) = p_total/m_total
Physics Check: In any collision or explosion, the center of mass of the system continues to move with the same velocity it had before the interaction. This provides a quick check on your momentum conservation calculations.
Explosion Problems
Explosions are essentially collisions running in reverse – a single object breaks apart into multiple pieces. The same conservation principles apply, but now we start with zero momentum and end with multiple moving objects.
Example Problem 4: A 60-kg astronaut floating in space throws a 5-kg tool eastward at 8 m/s. What’s the astronaut’s recoil velocity?
Solution:
- Initial momentum: p_initial = 0 (both at rest)
- Final momentum: p_final = (5)(8) + (60)(v_astronaut)
- Conservation: 0 = 40 + 60v_astronaut
- Result: v_astronaut = -0.67 m/s (westward)
Connections to Other Physics Units
Momentum doesn’t exist in isolation – it connects beautifully to concepts throughout AP Physics 1, creating a coherent understanding of mechanical systems.
Relationship to Newton’s Laws (Unit 2)
Newton’s second law in its most general form is F = dp/dt, not F = ma. The familiar F = ma only holds when mass remains constant. For systems with changing mass (like rockets), the momentum form becomes essential.
Newton’s third law directly leads to momentum conservation. When object A exerts force F_AB on object B, object B exerts force F_BA = -F_AB on object A. These equal and opposite forces create equal and opposite momentum changes, keeping total momentum constant.
Connection to Energy (Unit 5)
The relationship between momentum and kinetic energy appears in many contexts:
For a single object: KE = p²/(2m)
This relationship helps explain why momentum is conserved in all collisions while kinetic energy isn’t. The momentum-energy relationship becomes particularly important when analyzing elastic collisions and particle physics interactions.
Links to Rotational Motion (Units 6-7)
Linear momentum has a rotational analog called angular momentum (L = rp sin θ). Just as linear momentum is conserved in the absence of external forces, angular momentum is conserved in the absence of external torques. This principle explains everything from figure skaters pulling in their arms to the formation of galaxies.
Real-World Applications and Modern Physics
Understanding momentum opens doors to comprehending cutting-edge technology and natural phenomena across multiple scales.
Rocket Propulsion and Space Exploration
Rockets operate entirely on momentum conservation principles. By ejecting mass (propellant) at high velocity in one direction, rockets gain momentum in the opposite direction. The rocket equation, derived from momentum conservation, governs everything from launching satellites to planning Mars missions:
Δv = v_exhaust × ln(m_initial/m_final)
Real-World Physics: The SpaceX Falcon Heavy rocket must eject approximately 95% of its initial mass to achieve orbital velocity. This dramatic mass ratio demonstrates why rocket design remains so challenging – you need enormous amounts of propellant to accelerate relatively small payloads.
Particle Physics and Quantum Mechanics
In the subatomic world, momentum conservation helps physicists discover new particles and understand fundamental interactions. When high-energy particles collide in accelerators like the Large Hadron Collider, physicists use momentum conservation to identify the products of these collisions and infer the existence of particles that decay too quickly to detect directly.
Biomechanics and Sports Science
Athletes intuitively understand momentum principles, even if they don’t realize it. Gymnasts change their body configuration to alter their moment of inertia and rotation rate. Baseball pitchers and batters optimize the momentum transfer between ball and bat to maximize performance.
A typical baseball (mass ≈ 0.145 kg) leaving a bat at 45 m/s carries momentum of about 6.5 kg⋅m/s. The bat must impart this momentum through impulse during the roughly 0.001-second contact time, requiring average forces of several thousand Newtons.
Traffic Safety and Vehicle Design
Modern vehicle safety systems rely heavily on momentum and impulse principles. Adaptive cruise control systems calculate the momentum of approaching vehicles to prevent collisions. When crashes do occur, sophisticated sensor systems measure the momentum changes to deploy appropriate safety responses.
Common Mistakes and How to Avoid Them
Even advanced students make predictable errors when working with momentum. Recognizing these patterns will help you avoid similar mistakes on the AP exam.
Mistake 1: Forgetting Vector Nature
Wrong approach: Adding momentum magnitudes arithmetically in multi-dimensional problems
Correct approach: Always break momentum into components and add vectorially
When two objects collide at an angle, you cannot simply add their momentum magnitudes. You must consider both the x and y components of each momentum vector.
Mistake 2: Applying Conservation Incorrectly
Wrong approach: Using momentum conservation when significant external forces act on the system
Correct approach: Check that external forces are negligible or the time interval is very short
If a collision occurs on a rough surface with significant friction, you cannot ignore the friction force when applying momentum conservation.
Mistake 3: Confusing Elastic vs. Inelastic
Wrong approach: Assuming kinetic energy is conserved in all collisions
Correct approach: Check whether the collision is specified as elastic before using energy conservation
Unless explicitly stated or physically justified (like atomic collisions), assume collisions are inelastic and use only momentum conservation.
Mistake 4: Sign Errors in One-Dimensional Problems
Wrong approach: Using positive values for all velocities regardless of direction
Correct approach: Choose a coordinate system and stick to it consistently
Always define positive and negative directions clearly and maintain that convention throughout your solution.
Problem-Solving Strategy Box:
- Draw a diagram showing before and after
- Define your coordinate system clearly
- List known and unknown quantities
- Check whether the collision is elastic
- Write conservation equations
- Solve algebraically, then substitute numbers
- Check units and reasonableness of answer
Practice Problems for AP Exam Success
To master momentum concepts, you need to practice a variety of problem types that mirror those found on the AP Physics 1 exam. Here are representative problems with detailed solutions.
Multiple Choice Questions
Question 1: A 2-kg object moving at 6 m/s collides elastically with a 4-kg object at rest. After the collision, the 2-kg object moves at -2 m/s. What is the velocity of the 4-kg object after collision?
(A) 2 m/s
(B) 4 m/s
(C) 6 m/s
(D) 8 m/s
Solution:
Using momentum conservation:
Initial: (2)(6) + (4)(0) = 12 kg⋅m/s
Final: (2)(-2) + (4)(v₂) = -4 + 4v₂
Conservation: 12 = -4 + 4v₂ → v₂ = 4 m/s
Answer: (B) 4 m/s
Question 2: Which of the following best describes what happens to the center of mass of a system during an explosion?
(A) It accelerates in the direction of the largest fragment
(B) It remains stationary
(C) It moves with constant velocity
(D) It accelerates unpredictably
Solution: During an explosion, no external forces act on the system, so momentum is conserved. This means the center of mass continues to move with whatever velocity it had before the explosion.
Answer: (C) It moves with constant velocity
Free Response Questions
Question 3: A 1,000-kg car traveling north at 25 m/s collides with a 1,500-kg truck traveling east at 20 m/s. The vehicles stick together after the collision.
(a) Calculate the velocity (magnitude and direction) of the combined vehicles immediately after collision.
(b) Calculate the kinetic energy lost in the collision.
(c) Explain physically where this energy went.
Solution:
(a) Velocity after collision:
Using component form with north = +y, east = +x:
Initial momentum components:
- Car: pₓ = 0, pᵧ = (1,000)(25) = 25,000 kg⋅m/s
- Truck: pₓ = (1,500)(20) = 30,000 kg⋅m/s, pᵧ = 0
- Total: pₓ = 30,000 kg⋅m/s, pᵧ = 25,000 kg⋅m/s
Final momentum:
Combined mass = 2,500 kg
- pₓ = (2,500)vₓ = 30,000 → vₓ = 12 m/s
- pᵧ = (2,500)vᵧ = 25,000 → vᵧ = 10 m/s
Magnitude: v = √[(12)² + (10)²] = √244 = 15.6 m/s
Direction: θ = tan⁻¹(10/12) = 39.8° north of east
(b) Kinetic energy lost:
Initial KE:
- Car: ½(1,000)(25)² = 312,500 J
- Truck: ½(1,500)(20)² = 300,000 J
- Total: 612,500 J
Final KE: ½(2,500)(15.6)² = 304,200 J
Energy lost: 612,500 – 304,200 = 308,300 J
(c) Physical explanation:
The lost kinetic energy was converted to other forms during the collision: deformation of the vehicle bodies (plastic deformation work), heat generated by friction and compression, sound waves produced by the impact, and vibrations throughout both vehicles. This energy transformation explains why collisions cause damage even when momentum is perfectly conserved.
Advanced Topics: Beyond the AP Exam
While these topics exceed AP Physics 1 requirements, understanding them deepens your appreciation for momentum’s fundamental role in physics.
Relativistic Momentum
At very high speeds (approaching the speed of light), the classical momentum formula p = mv must be modified:
p = γmv = mv/√(1 – v²/c²)
This relativistic correction becomes significant when v > 0.1c (about 30,000 km/s). Even at these extreme speeds, momentum is still conserved, but its calculation requires Einstein’s special relativity.
Quantum Momentum
In quantum mechanics, momentum and position are related through Heisenberg’s uncertainty principle: Δx Δp ≥ ħ/2. This fundamental limit means we cannot simultaneously know both the exact position and momentum of a particle with perfect precision.
Conservation Laws and Symmetries
Emmy Noether’s theorem connects conservation laws to symmetries in nature. Momentum conservation emerges from the homogeneity of space – physics is the same everywhere in the universe. This deep connection between symmetry and conservation represents one of physics’ most beautiful insights.
Experimental Design and Laboratory Applications
The AP Physics 1 exam often includes questions about designing experiments to investigate momentum conservation. Understanding common experimental approaches will prepare you for these questions.
Classic Momentum Experiments
Air Track Collisions: Linear air tracks minimize friction, allowing nearly perfect momentum conservation studies. Students can verify conservation laws using photogates to measure velocities before and after collisions.
Ballistic Pendulum: This classic apparatus measures projectile velocity by observing how high a pendulum swings after being struck. The analysis combines momentum conservation (during collision) with energy conservation (during pendulum swing).
Two-Dimensional Collision Table: Pucks on air hockey tables allow investigation of momentum conservation in two dimensions. Video analysis software can track puck positions and calculate velocities throughout the collision process.
Data Analysis Considerations
Real experimental data never perfectly obeys theoretical predictions due to:
- Measurement uncertainty: Timer resolution, ruler precision, and human reaction time
- Systematic errors: Friction, air resistance, and equipment calibration
- Random errors: Statistical variations in repeated measurements
When designing momentum experiments, consider these sources of uncertainty and plan multiple trials with statistical analysis.

Error Analysis in Momentum Experiments
Percent error calculations help evaluate experimental success:
Percent Error = |Experimental Value – Theoretical Value|/Theoretical Value × 100%
For momentum conservation experiments, errors below 5% typically indicate successful verification of the conservation law, while larger errors suggest significant systematic problems.
Study Strategies and Exam Preparation
Mastering momentum concepts requires both conceptual understanding and problem-solving practice. Here’s how to structure your preparation for maximum effectiveness.
Conceptual Mastery Checklist
Before diving into complex problems, ensure you understand these fundamental concepts:
- [ ] Momentum is a vector quantity with both magnitude and direction
- [ ] Impulse equals the change in momentum (J = Δp = FΔt)
- [ ] Momentum is conserved when net external force is zero
- [ ] Kinetic energy is conserved only in elastic collisions
- [ ] The center of mass moves with constant velocity in isolated systems
- [ ] Internal forces cannot change the total momentum of a system
Problem-Solving Progression
Level 1: One-dimensional collisions with given masses and velocities
Level 2: Two-dimensional collisions requiring vector analysis
Level 3: Multi-step problems with several collisions or explosions
Level 4: Problems combining momentum with energy conservation
Level 5: Experimental design and data analysis questions
Work through problems systematically, focusing on understanding rather than memorization. Each solution should tell a complete physical story.
Mathematical Skills Review
Momentum problems require confident use of:
- Vector addition: Components and magnitude/direction calculations
- Trigonometry: Finding angles and components in 2D problems
- Algebra: Solving systems of equations with multiple unknowns
- Graphical analysis: Interpreting force vs. time graphs to find impulse
Practice these mathematical techniques in physics contexts rather than abstract math problems.
Common AP Exam Question Types
Type 1: Quantitative collision problems (25% of momentum questions)
- Given: masses and initial velocities
- Find: final velocities or momentum changes
- Skills: Vector analysis, conservation laws
Type 2: Conceptual reasoning (30% of momentum questions)
- Ranking tasks comparing momentum or impulse
- Explaining physical phenomena using momentum principles
- Identifying when conservation laws apply
Type 3: Experimental design (20% of momentum questions)
- Planning investigations of momentum conservation
- Analyzing data from collision experiments
- Identifying sources of experimental error
Type 4: Graphical analysis (15% of momentum questions)
- Interpreting force vs. time graphs to find impulse
- Using position or velocity graphs to calculate momentum changes
- Creating graphs to represent collision data
Type 5: Multi-concept problems (10% of momentum questions)
- Combining momentum with energy conservation
- Connecting momentum to rotational motion
- Applying momentum principles to complex systems
Quick Calculation Formulas:
- Momentum: p = mv
- Impulse: J = FΔt = Δp
- Conservation: Σp_initial = Σp_final
- Elastic collision: KE conserved
- Center of mass velocity: v_cm = p_total/m_total
Advanced Problem-Solving Strategies
For the most challenging AP exam problems, these advanced strategies will give you an edge.
The “Momentum Accounting” Method
For complex multi-object systems, create a “momentum ledger” tracking each object’s momentum before and after interactions:
| Object | Mass | v_initial | p_initial | v_final | p_final |
|---|---|---|---|---|---|
| 1 | m₁ | v₁ᵢ | m₁v₁ᵢ | v₁f | m₁v₁f |
| 2 | m₂ | v₂ᵢ | m₂v₂ᵢ | v₂f | m₂v₂f |
| Total | — | — | Σpᵢ | — | Σpf |
This systematic approach prevents errors and makes complex problems manageable.
Dimensional Analysis as a Check
Always verify that your momentum calculations have correct units:
- Momentum: [kg⋅m/s] or [N⋅s]
- Impulse: [N⋅s] or [kg⋅m/s]
- Force: [N] or [kg⋅m/s²]
Dimensional inconsistencies immediately reveal algebraic errors.
Limiting Case Analysis
Test your solutions by considering extreme cases:
- What happens if one mass becomes very large?
- What if one object is initially at rest?
- What if the collision is perfectly elastic vs. perfectly inelastic?
Your mathematical solutions should behave sensibly in these limits.
Conclusion: Momentum as a Gateway to Advanced Physics
As you complete your study of linear momentum, you’re not just mastering another AP Physics 1 topic -you’re developing intuition for one of nature’s most fundamental principles. The conservation of momentum, along with energy conservation, governs everything from atomic interactions to the motion of galaxies.
The problem-solving skills you’ve developed – systematic analysis, vector thinking, and conservation reasoning – will serve you well in advanced physics courses and scientific careers. Whether you’re planning to study engineering, medicine, or pure physics, the momentum concepts you’ve mastered form part of the essential foundation for understanding our physical world.
Your Next Steps
Final Exam Success Tips
Time Management: Momentum problems often require multiple steps. Practice working efficiently while maintaining accuracy. Don’t spend too much time on any single calculation.
Partial Credit Strategy: Even if you can’t complete a solution, show your understanding by:
- Drawing clear diagrams
- Writing conservation equations
- Explaining your reasoning in words
- Setting up the problem correctly even if arithmetic becomes complex
Common Trap Avoidance:
- Always check whether collisions are elastic or inelastic
- Remember that momentum conservation applies to each coordinate direction independently
- Don’t forget about the vector nature of momentum in 2D problems
- Verify that your final answers have reasonable magnitudes and directions
The principles you’ve learned in this unit represent some of humanity’s greatest intellectual achievements – the recognition that certain quantities remain constant even as the world changes around them. This insight has revolutionized our understanding of everything from atomic structure to stellar evolution.
As you continue your physics journey, remember that momentum conservation isn’t just a formula to memorize – it’s a window into the deep symmetries and patterns that govern our universe. Master these concepts not just for the exam, but for the profound understanding they provide about the nature of motion, force, and change itself.
Your thorough preparation in momentum will pay dividends not only on the AP exam but throughout your scientific education. The analytical thinking, mathematical problem-solving, and physical intuition you’ve developed here form the foundation for advanced topics in physics, engineering, and related fields.
Good luck with your continued studies, and remember: in physics, as in life, momentum matters!
Recommended –


1 thought on “AP Physics 1 Unit 4: Linear Momentum – The Ultimate Guide to Mastering Conservation Laws”