Class 12 Physics Chapter 13 Nuclei – NCERT Solutions: Complete Guide on Nuclear Physics, Radioactivity & Reactions

The Hidden World of Nuclear Physics Around You

Have you ever wondered what makes the sun shine continuously for billions of years? Or how doctors can see inside your body using radioactive tracers? The answer lies in the fascinating world of nuclear physics – specifically, in understanding the nucleus of an atom. Every moment of your life, you’re surrounded by nuclear phenomena. The carbon in your body contains radioactive carbon-14 that scientists use for dating, smoke detectors in your home use americium-241, and the energy powering nuclear plants comes from the same processes happening in stellar cores.

Chapter 13 of CBSE Class 12 Physics takes you deep into this microscopic realm where tremendous forces operate and where Einstein’s famous equation E=mc² becomes a practical reality. You’ll discover why some nuclei are stable while others spontaneously decay, releasing energy in the process. This chapter isn’t just about memorizing equations – it’s about understanding the fundamental forces that shape our universe and power the technologies that define modern civilization.

From medical imaging to carbon dating, from nuclear power plants to stellar nucleosynthesis, nuclear physics bridges the gap between the atomic world and cosmic phenomena. As you master these concepts, you’ll gain insights into both the smallest and largest scales of our universe.

Learning Objectives

By the end of this comprehensive study guide, you will be able to:

• Understand the composition and properties of atomic nuclei including size, mass, and density
• Analyze nuclear binding energy calculations and their significance in nuclear stability
• Master the concepts of mass-energy equivalence and mass defect in nuclear processes
• Explain different types of radioactive decay (alpha, beta, and gamma) with their characteristics
• Apply radioactive decay laws and calculate half-life, decay constant, and activity
• Solve problems involving nuclear reactions, Q-values, and conservation laws
• Understand nuclear fission and fusion processes with their energy calculations
• Connect nuclear physics concepts to real-world applications and technologies
• Develop problem-solving strategies specific to nuclear physics calculations
• Prepare effectively for CBSE Board examinations with confidence

1: Nuclear Fundamentals – Inside the Atom’s Core

Understanding Nuclear Structure

The nucleus sits at the heart of every atom, containing nearly all the atom’s mass in an incredibly tiny volume. Think of it this way: if an atom were the size of a football stadium, the nucleus would be smaller than a marble at the center. Yet this tiny region determines an element’s identity and governs its chemical properties.

The nucleus consists of two types of particles collectively called nucleons:

• Protons: Positively charged particles with charge +e (1.6 × 10^-19 C)
• Neutrons: Electrically neutral particles with nearly the same mass as protons

[EQUATION: Nuclear Notation: ᴬ_Z X where A = mass number, Z = atomic number, X = element symbol]

The atomic number Z represents the number of protons, which defines the element. The mass number A represents the total number of nucleons (protons + neutrons). The number of neutrons N = A – Z.

Nuclear Size and Density

Nuclear radius follows an empirical relationship that might surprise you. Unlike atomic orbitals, nuclear size increases with the number of nucleons:

[EQUATION: Nuclear Radius: R = R₀A^(1/3) where R₀ = 1.2 × 10^-15 m]

This cube-root relationship tells us something profound: nuclear density remains approximately constant regardless of nuclear size. It’s as if nucleons are incompressible spheres packed together.

Physics Check:
Quick Verification: Calculate the radius of ¹²C nucleus. Using the formula: R = 1.2 × 10^-15 × (12)^(1/3) = 1.2 × 10^-15 × 2.29 = 2.75 × 10^-15 m. Notice how incredibly small this is compared to the atomic radius of about 10^-10 m!

Nuclear Density Calculations

The nuclear density is remarkably uniform across all nuclei:

[EQUATION: Nuclear Density: ρ = M/V = A × u / (4/3)πR₀³A = 3u/(4πR₀³)]

Where u = 1.66 × 10^-27 kg (atomic mass unit)

This gives ρ ≈ 2.3 × 10^17 kg/m³ – about 100 trillion times denser than water! This incredible density explains why neutron stars, composed entirely of nuclear matter, can contain more mass than our sun in a sphere just 20 kilometers across.

Real-World Physics Box:
Neutron Star Connection: The matter in atomic nuclei has the same density as neutron star material. A teaspoon of neutron star matter would weigh about 6 billion tons – as much as Mount Everest!

2: Mass-Energy Equivalence and Nuclear Binding Energy

Einstein’s Revolutionary Insight

Einstein’s mass-energy equivalence fundamentally changed our understanding of nuclear processes. In nuclear physics, this isn’t just a theoretical concept – it’s a measurable, practical reality that explains nuclear stability and energy release.

[EQUATION: Mass-Energy Equivalence: E = mc² where c = 3 × 10⁸ m/s]

In nuclear calculations, we often use the convenient conversion:
[EQUATION: Energy Unit Conversion: 1 u = 931.5 MeV/c² = 931.5 MeV]

Mass Defect – The Missing Mass Mystery

Here’s something that initially puzzled scientists: when you carefully measure the mass of a nucleus, it’s always less than the sum of its constituent nucleons’ masses. This “missing mass” called mass defect (Δm) hasn’t vanished – it’s been converted to binding energy that holds the nucleus together.

[EQUATION: Mass Defect: Δm = Z×mₚ + N×mₙ – M_nucleus]

Where:

• mₚ = proton mass = 1.007276 u
• mₙ = neutron mass = 1.008665 u
• M_nucleus = actual nuclear mass

Binding Energy – Nature’s Nuclear Glue

The binding energy represents the energy required to completely separate all nucleons in a nucleus. Alternatively, it’s the energy released when free nucleons combine to form the nucleus.

[EQUATION: Binding Energy: BE = Δm × c² = Δm × 931.5 MeV]

Problem-Solving Strategy Box:
*Step-by-Step Binding Energy Calculation:

1. Identify Z, N, and A for the nucleus
2. Calculate theoretical mass = Z×mₚ + N×mₙ
3. Find actual nuclear mass (given or from tables)
4. Calculate mass defect = theoretical – actual
5. Convert to binding energy using BE = Δm × 931.5 MeV*

Binding Energy per Nucleon – The Stability Indicator

The binding energy per nucleon (BE/A) is crucial for understanding nuclear stability. This quantity varies with mass number in a characteristic curve that explains why certain nuclear processes release energy.

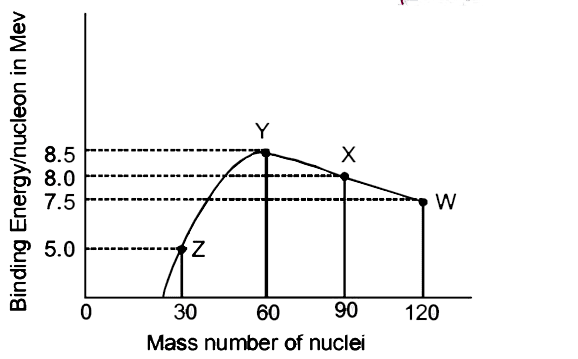
Key observations from the BE/A curve:

• Maximum occurs around A = 56 (Iron-56), making it the most stable nucleus
• Light nuclei (A < 20) can gain stability through fusion
• Heavy nuclei (A > 200) can gain stability through fission
• The curve explains why both fusion and fission release energy

Historical Context:
The binding energy curve was crucial in understanding stellar nucleosynthesis. Hans Bethe’s work on stellar fusion processes, guided by these energy considerations, earned him the 1967 Nobel Prize in Physics.

3: Radioactive Decay – Nature’s Nuclear Clock

The Phenomenon of Radioactivity

Radioactivity is nature’s way of transforming unstable nuclei into more stable configurations. Unlike chemical reactions that involve electrons, radioactive decay is a nuclear process that cannot be influenced by external conditions like temperature, pressure, or chemical environment.

Types of Radioactive Decay

Alpha Decay (α-decay)
In alpha decay, the nucleus emits an alpha particle (helium-4 nucleus: ²He⁴ or α).

[EQUATION: Alpha Decay: ᴬZ X → ᴬ⁻⁴{Z-2} Y + ²He⁴ + Q]

Alpha particles have:

• High ionizing power due to +2 charge
• Low penetrating power (stopped by paper or skin)
• Energy typically 4-7 MeV

Beta Decay (β-decay)
Two types exist:

Beta-minus decay (β⁻):
[EQUATION: β⁻ Decay: ᴬZ X → ᴬ{Z+1} Y + e⁻ + ν̄ₑ + Q]

Beta-plus decay (β⁺):
[EQUATION: β⁺ Decay: ᴬZ X → ᴬ{Z-1} Y + e⁺ + νₑ + Q]

The neutrino (ν) and antineutrino (ν̄) were postulated to conserve energy and momentum in beta decay.

Gamma Decay (γ-decay)
Gamma rays are high-energy electromagnetic radiation emitted when a nucleus transitions from an excited state to a lower energy state.

[EQUATION: Gamma Decay: ᴬ_Z X* → ᴬ_Z X + γ + Q]

Gamma rays have:

• No charge or mass
• Highest penetrating power
• Energy determined by nuclear energy level differences

Common Error Alert:
*Students often confuse the changes in atomic number for different decay types. Remember:

• α-decay: Z decreases by 2, A decreases by 4
• β⁻-decay: Z increases by 1, A unchanged
• β⁺-decay: Z decreases by 1, A unchanged
• γ-decay: No change in Z or A*

Radioactive Decay Law

Radioactive decay follows a statistical law – we cannot predict when a specific nucleus will decay, but we can predict the behavior of large numbers of nuclei with remarkable precision.

[EQUATION: Decay Law: N(t) = N₀e^(-λt)]

Where:

• N(t) = number of nuclei at time t
• N₀ = initial number of nuclei
• λ = decay constant (characteristic of the isotope)
• t = time elapsed

Activity and Half-Life

Activity (A) represents the rate of decay:
[EQUATION: Activity: A(t) = λN(t) = λN₀e^(-λt) = A₀e^(-λt)]

Unit: Becquerel (Bq) = 1 decay/second
Also used: Curie (Ci) = 3.7 × 10¹⁰ Bq

Half-life (t₁/₂) is the time required for half the nuclei to decay:
[EQUATION: Half-life: t₁/₂ = ln(2)/λ = 0.693/λ]

Physics Check Box:
Half-Life Verification: After one half-life, N = N₀/2. After two half-lives, N = N₀/4. After three half-lives, N = N₀/8. Notice the pattern: N(t) = N₀/2^(t/t₁/₂)

Mean Life and Relationships

The mean life (τ) represents the average lifetime of a nucleus:
[EQUATION: Mean Life: τ = 1/λ = t₁/₂/ln(2) = 1.44 × t₁/₂]

Real-World Physics:
Carbon Dating Application: Carbon-14 has a half-life of 5,730 years. Living organisms maintain a constant C-14/C-12 ratio through metabolism. After death, C-14 decays without replenishment, allowing archaeologists to determine the age of organic artifacts up to about 50,000 years old.

4: Nuclear Reactions and Q-Value Calculations

Understanding Nuclear Reactions

Nuclear reactions involve the transformation of atomic nuclei, differing fundamentally from chemical reactions. In nuclear reactions, the identity of elements changes, and the energy scales involved are millions of times larger than chemical processes.

[EQUATION: General Nuclear Reaction: A + a → B + b + Q]

Where A and a are reactants, B and b are products, and Q is the reaction energy.

Conservation Laws in Nuclear Reactions

Four fundamental conservation laws govern all nuclear reactions:

1. Conservation of Mass-Energy: Total mass-energy before = Total mass-energy after
2. Conservation of Electric Charge: Total charge before = Total charge after
3. Conservation of Mass Number: Total mass number before = Total mass number after
4. Conservation of Momentum: Total momentum before = Total momentum after

Q-Value Calculations

The Q-value represents the energy released (Q > 0) or absorbed (Q < 0) in a nuclear reaction:

[EQUATION: Q-Value: Q = (Mass of reactants – Mass of products) × c²]
[EQUATION: Q = (mₐ + mₐ – mᵦ – m_b) × 931.5 MeV]

Problem-Solving Strategy:
*Q-Value Calculation Steps:

1. Write the balanced nuclear equation
2. List masses of all reactants and products
3. Calculate total mass before and after reaction
4. Find mass difference: Δm = mass before – mass after
5. Convert to energy: Q = Δm × 931.5 MeV
6. Interpret result: Q > 0 (exothermic), Q < 0 (endothermic)*

Threshold Energy

For endothermic reactions (Q < 0), a minimum kinetic energy called threshold energy is required:

[EQUATION: Threshold Energy: Eₜₕ = -Q × (mₐ + mₐ + mᵦ + m_b)/(2mₐ)]

This accounts for momentum conservation requirements.

Types of Nuclear Reactions

Transmutation: Converting one element to another
Example: ¹⁴N + α → ¹⁷O + p (First artificial transmutation by Rutherford)

Neutron-Induced Reactions: Often have large cross-sections
Example: ²³⁵U + n → Fission products + neutrons + energy

Particle Bombardment: Using accelerated particles
Example: ²⁷Al + α → ³⁰P + n

5: Nuclear Fission – Splitting the Atom

The Discovery and Mechanism

Nuclear fission was discovered in 1938 by Otto Hahn and Fritz Strassmann, with theoretical explanation by Lise Meitner and Otto Frisch. Fission involves splitting a heavy nucleus into two or more lighter nuclei, typically releasing enormous energy.

[EQUATION: Typical U-235 Fission: ²³⁵U + n → ¹⁴¹Ba + ⁹²Kr + 3n + 200 MeV]

Why Fission Releases Energy

The binding energy per nucleon curve explains fission energy release. Heavy nuclei (A > 200) have lower BE/A than medium-mass nuclei (A ≈ 100). When a heavy nucleus splits into two medium-mass fragments, the total binding energy increases, releasing energy equal to the binding energy difference.

Chain Reaction and Critical Mass

Fission becomes self-sustaining when each fission event produces neutrons that cause additional fissions. The multiplication factor k determines the reaction behavior:

• k < 1: Subcritical (reaction dies out)
• k = 1: Critical (steady reaction rate)
• k > 1: Supercritical (exponentially increasing reaction rate)

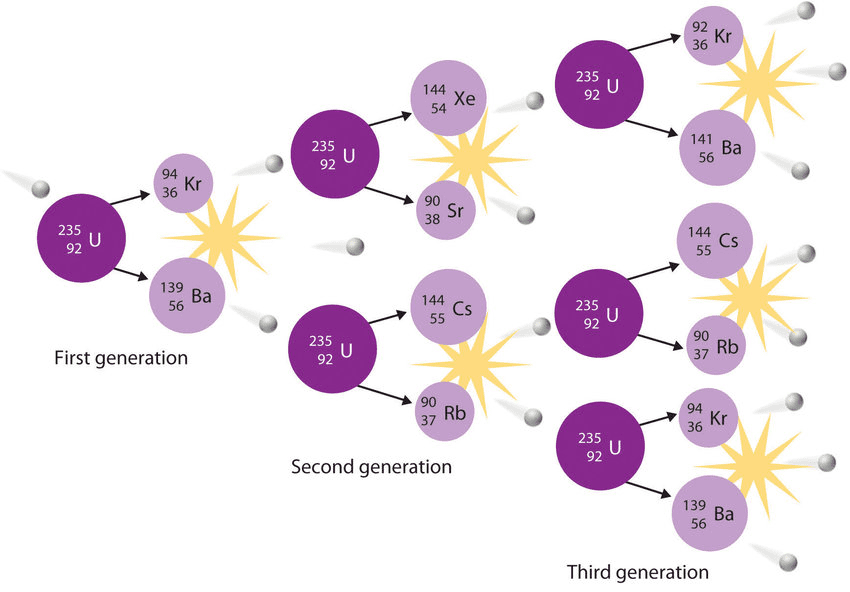
Critical mass is the minimum amount of fissile material needed to sustain a chain reaction, depending on:

• Material purity and isotopic composition
• Geometry (spherical shape minimizes neutron escape)
• Presence of neutron moderators or reflectors

Controlled vs. Uncontrolled Fission

Nuclear Reactors (controlled fission):

• Use control rods to absorb excess neutrons
• Maintain k ≈ 1 for steady power output
• Include coolant systems to remove heat
• Convert nuclear energy to electricity

Nuclear Weapons (uncontrolled fission):

• Achieve k >> 1 for explosive energy release
• Use sophisticated timing and compression techniques
• Release enormous energy in microseconds

Real-World Physics:
Nuclear Power Statistics: A single uranium pellet the size of a fingertip contains as much energy as a ton of coal. France generates about 70% of its electricity from nuclear power, demonstrating the practical application of controlled fission.

6: Nuclear Fusion – The Power of Stars

Fusion Fundamentals

Nuclear fusion combines light nuclei to form heavier nuclei, releasing energy because the products have higher binding energy per nucleon than the reactants. Fusion is the energy source powering the sun and all main-sequence stars.

Coulomb Barrier Challenge

For fusion to occur, nuclei must overcome the strong electrostatic repulsion (Coulomb barrier). The barrier height depends on the charges of the fusing nuclei:

[EQUATION: Coulomb Barrier Height: E_c ≈ 1.44 Z₁Z₂/r₀ MeV]

Where Z₁ and Z₂ are the atomic numbers and r₀ is the nuclear radius sum.

Stellar Fusion Processes

Proton-Proton Chain (dominant in stars like our sun):
[EQUATION: Overall: 4¹H → ⁴He + 2e⁺ + 2νₑ + 26.7 MeV]

This occurs through several intermediate steps involving deuterium and tritium formation.

CNO Cycle (dominant in massive stars):
Uses carbon, nitrogen, and oxygen nuclei as catalysts to convert hydrogen to helium.

Terrestrial Fusion Reactions

Deuterium-Tritium Fusion (most promising for power generation):
[EQUATION: D-T Fusion: ²H + ³H → ⁴He + n + 17.6 MeV]

Deuterium-Deuterium Fusion:
[EQUATION: D-D Fusion: ²H + ²H → ³He + n + 3.3 MeV]
[EQUATION: D-D Fusion: ²H + ²H → ³H + p + 4.0 MeV]

Conditions for Sustained Fusion

The Lawson Criterion defines the conditions needed for energy-producing fusion:
[EQUATION: Lawson Criterion: nτT > 10²¹ m⁻³·s·K]

Where:

• n = plasma density
• τ = confinement time
• T = temperature

This requires temperatures exceeding 100 million Kelvin and sophisticated confinement methods.

Fusion Reactor Approaches

Magnetic Confinement (Tokamaks):

• Use powerful magnetic fields to confine hot plasma
• Examples: ITER project, JET facility
• Aim for controlled, steady-state fusion

Inertial Confinement (Laser Fusion):

• Compress fuel pellets using intense laser pulses
• Achieve fusion through extremely high density and temperature
• Examples: National Ignition Facility (NIF)

Historical Context:
Fusion Energy Timeline: Hans Bethe explained stellar fusion in 1938. The first controlled fusion reaction was achieved in 1951. The ITER project, beginning operations in the 2020s, represents humanity’s most ambitious attempt to harness fusion for clean energy production.

7: Advanced Nuclear Applications and Technology

Medical Applications of Nuclear Physics

Diagnostic Imaging:

• PET Scans: Use positron-emitting isotopes like F-18
• SPECT: Single Photon Emission Computed Tomography using gamma emitters
• Radiopharmaceuticals: Tc-99m for various organ imaging

Cancer Treatment:

• External Beam Therapy: High-energy photons or particle beams
• Brachytherapy: Radioactive sources placed near tumors
• Radiopharmaceutical Therapy: Targeted delivery using isotopes like I-131

Nuclear Dating Methods

Carbon-14 Dating (organic materials up to 50,000 years):
[EQUATION: Age Calculation: t = (1/λ) × ln(N₀/N) = 8267 × ln(A₀/A) years]

Potassium-Argon Dating (rocks millions to billions of years old):
Uses the decay of K-40 to Ar-40 with a half-life of 1.25 billion years.

Uranium-Lead Dating (oldest rocks):
Uses the U-238 decay chain with a half-life of 4.5 billion years.

Nuclear Security and Safety

Radiation Detection:

• Geiger-Müller counters for general radiation
• Scintillation detectors for gamma spectroscopy
• Neutron detectors for fissile material identification

Radiation Protection Principles (ALARA):

• Time: Minimize exposure duration
• Distance: Inverse square law reduces exposure
• Shielding: Use appropriate materials (lead, concrete, water)

Real-World Physics:
Nuclear Forensics: Scientists can determine the origin and history of nuclear materials by analyzing isotopic signatures. This technique helps prevent nuclear proliferation and investigate nuclear security incidents.

8: Laboratory Applications and Experimental Techniques

Nuclear Physics Experiments in CBSE Labs

Geiger-Müller Counter Experiments:

• Measure background radiation
• Investigate inverse square law for gamma sources
• Study absorption of beta particles in matter
• Verify radioactive decay statistics

Measuring Nuclear Properties

Mass Spectrometry: Determines isotopic masses and abundances

• Measures mass-to-charge ratios precisely
• Confirms mass defect calculations
• Identifies unknown isotopes

Rutherford Scattering: Reveals nuclear size

• Alpha particles scattered by thin foils
• Large angle scattering indicates nuclear dimensions
• Led to nuclear model of the atom

Error Analysis in Nuclear Measurements

Statistical Uncertainty: Radioactive decay follows Poisson statistics
[EQUATION: Statistical Uncertainty: σ = √N where N is the count number]

Systematic Errors:

• Detector efficiency variations
• Background radiation fluctuations
• Source decay during measurement
• Geometric factors in counting

Problem-Solving Strategy Box:
*Experimental Design Checklist:

1. Identify all sources of uncertainty
2. Plan sufficient counting time for statistical accuracy
3. Account for background radiation
4. Consider radioactive decay during long measurements
5. Calibrate detectors with known sources
6. Repeat measurements for reliability verification*

Practice Problems Section

Multiple Choice Questions

Problem 1: The binding energy per nucleon is maximum for nuclei with mass number around:
a) 20
b) 56
c) 120
d) 238

Solution: Answer (b) 56. The binding energy per nucleon curve peaks around Iron-56, making it the most stable nucleus. This explains why both fusion of light nuclei and fission of heavy nuclei release energy.

Problem 2: In the nuclear reaction ²⁷Al + α → ³⁰P + n, the Q-value is +2.3 MeV. This means the reaction is:
a) Endothermic, requiring energy input
b) Exothermic, releasing energy
c) Neither endothermic nor exothermic
d) Impossible due to conservation laws

Solution: Answer (b) Exothermic, releasing energy. A positive Q-value indicates that the reaction releases energy equal to the mass difference between reactants and products.

Problem 3: The half-life of a radioactive sample is 20 years. What fraction remains after 60 years?
a) 1/6
b) 1/8
c) 1/3
d) 1/4

Solution: Answer (b) 1/8. After 60 years = 3 half-lives, the remaining fraction is (1/2)³ = 1/8 of the original amount.

Numerical Problems with Complete Solutions

Problem 4: Calculate the binding energy of ⁴He nucleus.
Given: Mass of proton = 1.007276 u, Mass of neutron = 1.008665 u, Mass of ⁴He = 4.002603 u

Solution:
Step 1: Identify the composition
⁴He has Z = 2 protons, N = 2 neutrons

Step 2: Calculate theoretical mass
Theoretical mass = 2 × 1.007276 + 2 × 1.008665 = 2.014552 + 2.01733 = 4.031882 u

Step 3: Find mass defect
Mass defect (Δm) = 4.031882 – 4.002603 = 0.029279 u

Step 4: Calculate binding energy
BE = 0.029279 × 931.5 MeV = 27.28 MeV

Step 5: Check reasonableness
BE per nucleon = 27.28/4 = 6.82 MeV/nucleon, which is reasonable for light nuclei.

Problem 5: A radioactive sample has an activity of 1000 Bq. If its half-life is 10 hours, what will be its activity after 30 hours?

Solution:
Step 1: Identify given information
Initial activity A₀ = 1000 Bq, t₁/₂ = 10 hours, time t = 30 hours

Step 2: Determine number of half-lives
Number of half-lives = t/t₁/₂ = 30/10 = 3

Step 3: Apply decay formula
A(t) = A₀ × (1/2)^(t/t₁/₂) = 1000 × (1/2)³ = 1000 × 1/8 = 125 Bq

Step 4: Alternative method using decay constant
λ = 0.693/t₁/₂ = 0.693/10 = 0.0693 h⁻¹
A(t) = A₀e^(-λt) = 1000 × e^(-0.0693×30) = 1000 × e^(-2.079) = 125 Bq

Problem 6: Calculate the Q-value for the nuclear reaction: ⁷Li + p → 2α
Given masses: ⁷Li = 7.016003 u, p = 1.007825 u, α = 4.002603 u

Solution:
Step 1: Write the balanced equation
⁷Li + ¹H → 2(⁴He)

Step 2: Calculate masses
Mass before reaction = 7.016003 + 1.007825 = 8.023828 u
Mass after reaction = 2 × 4.002603 = 8.005206 u

Step 3: Find mass defect
Δm = 8.023828 – 8.005206 = 0.018622 u

Step 4: Calculate Q-value
Q = 0.018622 × 931.5 MeV = 17.35 MeV

Step 5: Interpret result
Since Q > 0, this is an exothermic reaction releasing 17.35 MeV of energy.

Advanced Problem-Solving Scenarios

Problem 7: A nuclear power plant produces 1000 MW of electrical power with 33% efficiency. If each U-235 fission releases 200 MeV, how many U-235 nuclei undergo fission per second?

Solution:
Step 1: Calculate thermal power needed
Thermal power = Electrical power / Efficiency = 1000 MW / 0.33 = 3030 MW = 3.03 × 10⁹ W

Step 2: Convert energy per fission to Joules
Energy per fission = 200 MeV = 200 × 1.6 × 10⁻¹³ J = 3.2 × 10⁻¹¹ J

Step 3: Calculate fission rate
Fission rate = Power / Energy per fission = (3.03 × 10⁹) / (3.2 × 10⁻¹¹) = 9.47 × 10¹⁹ fissions/second

Step 4: Verify units and magnitude
The result represents about 10²⁰ nuclear reactions per second, which is reasonable for a large power plant.

Problem 8: Carbon-14 dating of a wooden artifact shows that its current C-14 activity is 25% of the activity in living wood. Determine the age of the artifact.
Given: Half-life of C-14 = 5730 years

Solution:
Step 1: Set up the decay equation
A(t)/A₀ = 0.25 = e^(-λt)

Step 2: Calculate decay constant
λ = 0.693/t₁/₂ = 0.693/5730 = 1.21 × 10⁻⁴ year⁻¹

Step 3: Solve for time
ln(0.25) = -λt
-1.386 = -1.21 × 10⁻⁴ × t
t = 1.386/(1.21 × 10⁻⁴) = 11,460 years

Step 4: Alternative approach using half-lives
Since A/A₀ = 0.25 = (1/2)², the artifact is 2 half-lives old
Age = 2 × 5730 = 11,460 years

Exam Preparation Strategies

Understanding CBSE Examination Patterns

Question Type Distribution:

• Multiple Choice Questions (20%): Test conceptual understanding
• Short Answer Questions (30%): Require definitions and brief explanations
• Long Answer Questions (50%): Involve detailed calculations and derivations

Common Topics in CBSE Exams:

1. Nuclear radius and density calculations
2. Mass-energy equivalence problems
3. Binding energy calculations
4. Radioactive decay law applications
5. Half-life and mean life relationships
6. Nuclear reaction Q-value calculations
7. Applications of nuclear physics

Common Examination Mistakes and Prevention

Common Error Alert Box:
*Frequent Student Mistakes:

1. Unit Confusion: Mixing up mass units (kg vs. u) and energy units (J vs. MeV)
   Prevention: Always write units and convert systematically
2. Sign Errors in Q-values: Confusing energy release vs. absorption
   Prevention: Remember Q = (reactant mass – product mass) × c²
3. Half-life Calculations: Using wrong formulas or number of half-lives
   Prevention: Always identify how many half-lives have elapsed
4. Conservation Law Violations: Not balancing mass number or charge
   Prevention: Check all conservation laws before solving*

Formula Sheet Organization

Essential Equations for Quick Reference:

1. Nuclear radius: R = R₀A^(1/3)
2. Mass-energy: E = mc², 1u = 931.5 MeV
3. Binding energy: BE = Δm × 931.5 MeV
4. Decay law: N(t) = N₀e^(-λt)
5. Half-life: t₁/₂ = 0.693/λ
6. Activity: A(t) = λN(t)
7. Q-value: Q = (mass before – mass after) × 931.5 MeV

Conclusion and Next Steps

Connecting to Advanced Physics

Nuclear physics serves as a bridge to several advanced topics you’ll encounter in higher studies:

Quantum Mechanics: Nuclear energy levels and wave functions
Particle Physics: Fundamental interactions and particle accelerators
Astrophysics: Stellar nucleosynthesis and neutron stars
Engineering: Nuclear reactor design and radiation shielding

Final Examination Confidence

You now possess a comprehensive understanding of nuclear physics that extends far beyond CBSE requirements. Your ability to calculate binding energies, predict radioactive decay, analyze nuclear reactions, and understand both fission and fusion processes positions you for success not only in examinations but in understanding one of physics’ most fascinating and practically important domains.

Remember that nuclear physics represents humanity’s deepest probe into matter’s fundamental nature. Every calculation you perform connects you to the same physical processes powering stars, enabling medical treatments, and potentially providing clean energy for future generations. The mathematical tools and conceptual frameworks you’ve mastered open doors to understanding phenomena from the smallest nuclear scales to the largest cosmic processes.

As you approach your CBSE examination, trust in your preparation and remember that nuclear physics problems follow logical patterns. Apply conservation laws systematically, check units carefully, and always consider whether your numerical answers make physical sense. The investment you’ve made in truly understanding these concepts, rather than merely memorizing formulas, will serve you well not only in examinations but throughout any future scientific endeavors.

The nucleus may be incredibly small, but your understanding of its behavior connects you to the grandest scales and most profound mysteries of our universe. Carry this knowledge forward with confidence and curiosity.

Recommended –

• CBSE Class 12 Physics Chapter 11: Dual Nature of Radiation and Matter – Complete Study Guide
• Atoms Class 12 Notes: NCERT Solutions, Atomic Models & Important Questions for CBSE Board Exams