Picture this: You’re watching your favorite athlete launch a basketball toward the hoop, or maybe you’re marveling at how your smartphone battery powers everything from your music to your GPS navigation. What do these seemingly different scenarios have in common? They’re all perfect examples of the fundamental physics concepts we’ll explore in AP Physics 1 Unit 3: Work, Energy, and Power.
Every time you climb stairs, ride a roller coaster, or even just lift your backpack, you’re experiencing the intricate dance between work, energy, and power that governs our physical world. These aren’t just abstract concepts locked away in textbooks – they’re the driving forces behind everything from the engines in our cars to the renewable energy systems that are reshaping our planet’s future.
In this comprehensive guide, we’ll unpack one of the most crucial and frequently tested units in AP Physics 1. Unit 3 serves as a bridge between the motion concepts you learned in kinematics and dynamics, and the more complex systems you’ll encounter later in the course. More importantly, mastering these energy concepts will give you powerful problem-solving tools that often provide elegant solutions to problems that might seem impossibly complex using force analysis alone.
Learning Objectives: What You’ll Master in This Unit
By the end of this deep dive into AP Physics 1 Unit 3, you’ll have developed a comprehensive understanding of energy concepts that will serve you well beyond the AP exam. Here’s what you’ll accomplish:
Conceptual Mastery Goals:
- Understand work as the transfer of energy due to force acting through displacement
- Distinguish between different forms of mechanical energy (kinetic and potential)
- Apply conservation of energy principles to analyze complex physical systems
- Connect power concepts to real-world applications in technology and biology
- Develop intuition for when energy methods provide simpler solutions than force analysis
Mathematical Proficiency Targets:
- Calculate work done by constant and variable forces using both algebraic and graphical methods
- Apply kinetic and potential energy formulas to solve multi-step problems
- Use conservation of energy to analyze systems where forces are difficult to determine directly
- Determine power requirements and efficiency in mechanical systems
- Interpret energy bar charts and graphs to understand system behavior
Problem-Solving Strategy Development:
- Learn when energy methods are more effective than Newtonian force analysis
- Master the systematic approach to energy conservation problems
- Develop skills in identifying and tracking energy transformations
- Practice experimental design focused on energy measurements and analysis
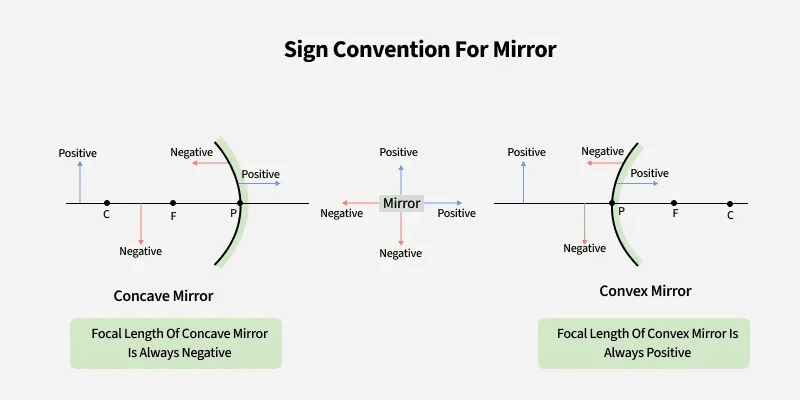
The Foundation: Understanding Work in Physics
When you hear the word “work” in everyday conversation, you might think about your job, homework, or physical labor. But in physics, work has a very specific and precise meaning that’s both more restrictive and more powerful than our everyday usage.
Physics Check: The Precise Definition of Work
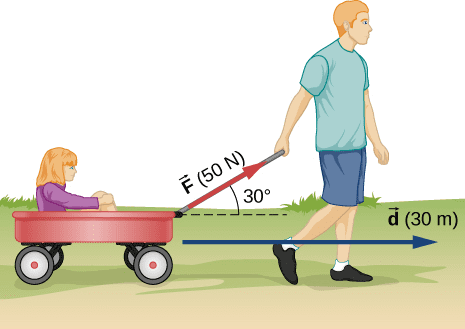
Work is the energy transferred to or from an object when a force acts on that object through a displacement. Mathematically, work equals the component of force in the direction of displacement multiplied by the magnitude of that displacement.
Let’s break this down with a scenario you can easily visualize. Imagine you’re helping a friend move by pushing a heavy box across the floor. You apply a force to the box, and the box moves some distance in response to your push. In this case, you’re doing positive work on the box because your force and the box’s displacement are in the same direction.
The mathematical expression for work done by a constant force is elegantly simple:
W = F⃗ · d⃗ = Fd cos θ
Where:
- W represents work (measured in joules)
- F is the magnitude of the applied force (in newtons)
- d is the magnitude of displacement (in meters)
- θ is the angle between the force vector and displacement vector
Real-World Physics: Why Carrying a Heavy Backpack Horizontally Involves No Work
Here’s something that might surprise you: when you carry a heavy backpack while walking across level ground, you’re doing zero work on the backpack from a physics perspective! This seems counterintuitive because you certainly feel like you’re working hard, and your muscles are definitely expending energy.
The key insight is that work requires force in the direction of motion. When you carry a backpack horizontally, you’re applying an upward force to support it against gravity, but the displacement is horizontal. Since the force and displacement are perpendicular (θ = 90°), and cos(90°) = 0, the work done is zero.
Your muscles feel tired because biological systems are inefficient – they must continuously contract and relax to maintain steady forces, converting chemical energy to heat. But from a pure physics standpoint, no mechanical work is being done on the backpack.
Work Done by Variable Forces: Beyond the Basics
While constant force situations are straightforward, many real-world scenarios involve forces that change as an object moves. The classic example that appears frequently on AP Physics 1 exams is the work done by a spring force, which varies linearly with displacement according to Hooke’s Law.
When force varies with position, we need to use a more sophisticated approach. The work becomes the area under a force vs. displacement graph, or mathematically:
W = ∫F(x)dx
For the specific case of a spring force (F = -kx), this integration yields:
W = ½kx²
This result appears so frequently in energy problems that it’s worth memorizing, but more importantly, understand that it represents the area under a triangular force vs. displacement graph.
Problem-Solving Strategy: Recognizing When to Use Work-Energy Methods
Here’s a crucial insight that will save you time and effort on the AP exam: work-energy methods are particularly powerful when you care about the final state of a system but don’t need to know the details of what happened during the process. If a problem asks about final speed, maximum height, or stopping distance, think energy first!
Consider this example: A block slides down a curved, frictionless track from rest. Using Newtonian methods, you’d need to analyze forces at every point along the curved path – a nightmare of changing angles and complex trigonometry. Using energy methods, you simply recognize that potential energy converts to kinetic energy, leading to a straightforward solution.
Kinetic Energy: The Energy of Motion
Kinetic energy represents one of the most intuitive forms of energy – it’s the energy an object possesses simply because it’s moving. Every moving object, from electrons in a wire to planets orbiting the sun, carries kinetic energy that depends on both its mass and speed.
The kinetic energy formula is beautifully simple:
KE = ½mv²
But don’t let this simplicity fool you into thinking kinetic energy is a trivial concept. The squared relationship with velocity has profound implications that show up repeatedly in physics problems and real-world applications.
Physics Check: Why Kinetic Energy Depends on v² Rather Than Just v
The squared relationship comes directly from the work-energy theorem and the fundamental relationship between force, acceleration, and displacement. When a constant force accelerates an object from rest, the work done equals the change in kinetic energy. Since acceleration produces velocity that increases linearly with time, but displacement increases as the square of time, the energy ends up depending on v².
This squared relationship explains why highway speed limits exist, why stopping distances increase dramatically with speed, and why kinetic weapons become devastatingly more powerful with higher velocities.
Real-World Physics: Understanding Vehicle Safety Through Kinetic Energy
Consider why automotive engineers obsess over vehicle weight and crash safety. A car traveling at 60 mph has four times the kinetic energy of the same car traveling at 30 mph, not twice as much. This means that in a collision, four times as much energy must be dissipated to bring the car to a stop.
Modern cars are designed with crumple zones that extend the time and distance over which this energy dissipation occurs, reducing the forces experienced by passengers. The physics principle is straightforward: if you can’t change the energy that must be dissipated, you can reduce the forces by increasing the time or distance over which the dissipation occurs.
Rotational Kinetic Energy: A Preview of Advanced Concepts
While AP Physics 1 focuses primarily on translational kinetic energy, it’s worth noting that rotating objects also possess rotational kinetic energy. This concept becomes crucial in AP Physics C, but understanding its existence helps explain why rolling objects behave differently from sliding objects.
A rolling ball has both translational kinetic energy (from its center-of-mass motion) and rotational kinetic energy (from its spinning motion). This is why a solid sphere rolls down an incline more slowly than a sliding block – some of the available potential energy goes into rotational rather than translational motion.
Potential Energy: Stored Energy in Position and Configuration
Potential energy represents stored energy that results from an object’s position or configuration within a force field. While kinetic energy is energy of motion, potential energy is energy of position, waiting to be converted into other forms of energy when the system configuration changes.
Gravitational Potential Energy: The Energy of Height
Near Earth’s surface, gravitational potential energy follows the familiar formula:
PE_gravity = mgh
Where h represents height above some chosen reference level. This formula assumes a constant gravitational field, which is an excellent approximation for objects moving relatively small distances near Earth’s surface.
Common Physics Mistake Alert: Choosing Reference Levels
One of the most frequent sources of confusion in energy problems involves choosing an appropriate reference level for potential energy. Remember that only changes in potential energy have physical meaning – the absolute value depends on your arbitrary choice of where to set PE = 0.
Choose your reference level strategically to simplify calculations. Often, setting the lowest point in the problem as h = 0 works well, but sometimes choosing the starting or ending position as the reference makes the math cleaner.
Problem-Solving Strategy: The Energy Bar Chart Method
Energy bar charts provide a powerful visual tool for tracking energy transformations throughout a problem. Create vertical bars showing kinetic energy, potential energy, and any non-conservative energy losses at key points in the motion.
For example, consider a ball thrown upward:
- Initially: mostly kinetic energy, some potential energy
- At maximum height: zero kinetic energy, maximum potential energy
- Upon return: kinetic energy restored, potential energy minimized
Elastic Potential Energy: Energy Stored in Deformation
When you compress a spring, stretch a rubber band, or bend a diving board, you’re storing elastic potential energy in the deformed object. This energy can be recovered when the object returns to its original shape, making elastic potential energy a form of mechanical energy that obeys conservation principles.
For an ideal spring following Hooke’s Law (F = -kx), the elastic potential energy is:
PE_elastic = ½kx²
This parabolic relationship means that doubling the compression or extension quadruples the stored energy – a relationship that has important implications for everything from shock absorbers to archery bows.
Real-World Physics: Springs in Automotive Engineering
Car suspension systems demonstrate elegant applications of elastic potential energy. When your car hits a bump, the springs compress, storing the kinetic energy of the sudden upward motion as elastic potential energy. Shock absorbers then dissipate this energy gradually, preventing the car from bouncing uncontrollably.
Racing cars use stiffer springs (higher k values) that store more energy for a given compression, providing better handling but a harsher ride. The trade-off between comfort and performance ultimately comes down to energy storage and dissipation characteristics.
The Principle of Conservation of Energy: Nature’s Ultimate Bookkeeping System
Conservation of energy stands as one of the most profound and useful principles in all of physics. It states that energy cannot be created or destroyed, only transformed from one form to another or transferred from one object to another. This principle provides a powerful problem-solving tool that often simplifies complex mechanical problems.
Physics Check: The Work-Energy Theorem
The work-energy theorem provides the mathematical foundation for energy conservation:
W_net = ΔKE = KE_final – KE_initial
This theorem tells us that the net work done on an object equals its change in kinetic energy. When combined with careful identification of all energy forms in a system, it leads directly to conservation of energy.
Conservative vs. Non-Conservative Forces: The Key Distinction
Understanding the difference between conservative and non-conservative forces is crucial for applying energy conservation correctly.
Conservative forces are path-independent – the work they do depends only on the starting and ending positions, not on the specific route taken. Gravity and spring forces are the primary conservative forces in AP Physics 1. For conservative forces, we can define potential energy functions that allow us to use energy conservation methods.
Non-conservative forces are path-dependent – the work they do depends on the specific path taken. Friction and air resistance are the most common non-conservative forces. These forces typically convert mechanical energy into thermal energy, causing the total mechanical energy of a system to decrease.
Conservation of Mechanical Energy Formula:
For systems with only conservative forces:
E_initial = E_final
KE_i + PE_i = KE_f + PE_f
For systems with non-conservative forces:
E_initial = E_final + E_dissipated
KE_i + PE_i = KE_f + PE_f + W_friction
[INSERT DIAGRAM: Two scenarios side by side – frictionless track showing energy conservation with equal total energy bars, and track with friction showing decreasing total energy with energy lost to heat]
Advanced Energy Conservation: Systems with Multiple Objects
Real-world systems often involve multiple objects exchanging energy. Consider a collision between two cars, or a person jumping off a diving board. In these cases, you must account for the kinetic and potential energy of all objects in the system.
The key insight is to define your system carefully. If you include all interacting objects within your system boundary, internal forces (like the forces between colliding objects) become internal energy transfers rather than external work, allowing you to apply conservation of energy to the entire system.
Real-World Physics: Regenerative Braking in Electric Vehicles
Electric and hybrid vehicles demonstrate sophisticated energy conservation in action. During normal braking, kinetic energy converts to waste heat in friction brakes. But regenerative braking systems reverse this process – the electric motor acts as a generator, converting the vehicle’s kinetic energy back into electrical energy stored in the battery.
This process isn’t 100% efficient due to electrical resistance and other losses, but it can recover 60-70% of the braking energy, significantly extending the vehicle’s range. The physics principle is straightforward energy conversion: kinetic → electrical → chemical (battery storage) → electrical → kinetic (acceleration).
Power: The Rate of Energy Transfer
Power measures how quickly energy is transferred or work is done. While work and energy tell us how much, power tells us how fast. This distinction proves crucial in understanding everything from electric motors to biological metabolism.
The basic definition of power is:
P = W/t = ΔE/t
For constant power, this simplifies our calculations significantly. But when power varies with time, we need more sophisticated approaches.
Alternative Power Formula:
When force and velocity are involved:
P = F⃗ · v⃗ = Fv cos θ
This formula proves particularly useful for problems involving vehicles, since it directly relates the driving force, speed, and power requirements.
Physics Check: Understanding Units and Scale
Power is measured in watts (W), where 1 watt = 1 joule/second. To develop intuition for power scales:
- Human muscle power: ~100-500 watts (sustained)
- Household appliances: 100-3000 watts
- Car engines: 50,000-500,000 watts (67-670 horsepower)
- Power plants: 10⁹-10⁹ watts (1-10 gigawatts)
Efficiency: Real-World Energy Conversion
No real energy conversion process is perfectly efficient. Some energy always converts to less useful forms, typically heat. Efficiency quantifies how much of the input energy converts to useful output energy:
Efficiency = (Useful Energy Output)/(Total Energy Input) × 100%
Real-World Physics: The Efficiency Challenge in Energy Systems
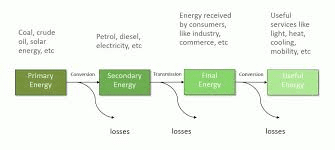
Consider the journey of energy from a power plant to your smartphone:
- Coal/gas → heat (~40% efficient)
- Heat → electricity (~35% efficient)
- Electricity transmission (~92% efficient)
- Charging circuit (~85% efficient)
- Battery storage/retrieval (~95% efficient)
The overall efficiency from fuel to stored electrical energy is roughly 40% × 35% × 92% × 85% × 95% ≈ 10%. This analysis explains why energy conservation and renewable sources are so important – most of our energy is lost as waste heat in conversion processes.
Problem-Solving Mastery: Systematic Approaches to Energy Problems
Success in AP Physics 1 Unit 3 requires developing systematic problem-solving strategies that can handle the wide variety of energy problems you’ll encounter. Here’s a proven approach that works consistently across different problem types.
The Universal Energy Problem-Solving Method
Step 1: Define Your System
Clearly identify what objects are included in your analysis. Are you analyzing a single block, a block-and-spring system, or a more complex multi-object system? Your choice affects which forces are internal (and thus don’t do net work) versus external.
Step 2: Identify Initial and Final States
Determine the relevant information about energy and motion at the beginning and end of the process you’re analyzing. Often, one of these states involves zero kinetic energy (at rest) or zero potential energy (at the reference level).
Step 3: Catalog All Energy Forms
List all forms of energy present in both initial and final states:
- Kinetic energy (translational)
- Gravitational potential energy
- Elastic potential energy
- Any other relevant energy forms
Step 4: Account for Non-Conservative Forces
Identify any non-conservative forces (friction, air resistance, etc.) and calculate the work they do. This work represents energy that leaves the mechanical system, usually as heat.
Step 5: Apply Conservation of Energy
Write the energy conservation equation appropriate for your system:
- If only conservative forces: E_initial = E_final
- If non-conservative forces present: E_initial = E_final + Energy_dissipated
Step 6: Solve and Check
Solve algebraically when possible, then substitute numerical values. Always check units and consider whether your answer makes physical sense.
Problem-Solving Strategy: Working Backwards from Energy
Sometimes the most efficient approach is to work backwards from the final energy state. If you know where an object ends up, you can often determine what its initial conditions must have been, even when the intermediate motion is complex.
Example: A ball launched from ground level just barely clears a 10-meter wall before landing back at ground level 50 meters away. What was its initial kinetic energy? Working backwards from the constraint that it “just barely” clears the wall gives you information about the trajectory that leads directly to the initial energy.
Advanced Problem-Solving: Energy in Collision and Explosion Problems
While AP Physics 1 doesn’t require detailed collision analysis, understanding energy conservation in collisions provides insight into when mechanical energy is conserved versus when it’s dissipated.
Elastic collisions conserve both momentum and kinetic energy. These are idealized but provide useful approximations for hard objects moving at moderate speeds.
Inelastic collisions conserve momentum but not kinetic energy. Some kinetic energy converts to other forms (heat, sound, permanent deformation). Perfectly inelastic collisions involve objects sticking together after collision.
The key insight for AP Physics 1 is recognizing that collision problems often involve energy considerations even when they’re primarily momentum problems.
Common Misconceptions and How to Avoid Them
Understanding physics requires overcoming intuitive but incorrect ideas about how energy works. Here are the most common misconceptions that can trip up AP Physics 1 students:
Misconception 1: “Work requires motion”
Correction: Work requires force and displacement, but the displacement doesn’t have to be in the same direction as the force. You can do negative work by applying force opposite to motion (like brakes on a car).
Misconception 2: “Energy is used up when you do work”
Correction: Energy is conserved – it transforms from one form to another but is never destroyed. When you “use” energy, you’re actually converting it to less useful forms, typically heat.
Misconception 3: “Potential energy depends on the path taken”
Correction: Potential energy is a state function – it depends only on position, not on how you got there. This path independence is what makes energy methods so powerful.
Misconception 4: “Power and energy are the same thing”
Correction: Power is the rate of energy transfer. A small motor running for a long time can transfer the same energy as a large motor running briefly, but they have very different power ratings.
Common Physics Mistake Alert: Sign Conventions in Energy Problems
Be careful with signs when dealing with work and energy. Positive work increases kinetic energy, while negative work decreases it. When an object moves upward, gravitational potential energy increases. When a spring is compressed or stretched from its natural length, elastic potential energy increases.
Experimental Design and Data Analysis in Energy Studies
AP Physics 1 emphasizes experimental design and data analysis skills alongside conceptual understanding. Energy conservation provides an excellent framework for designing controlled experiments and analyzing real-world data.
Classic Energy Experiments for AP Physics 1
The Pendulum Experiment
A simple pendulum demonstrates energy conservation beautifully. At the highest points of its swing, energy is primarily gravitational potential. At the bottom, energy is primarily kinetic. Measuring the maximum angle and using energy conservation, you can predict the speed at the bottom without timing the motion.
Experimental Design Considerations:
- How do you minimize air resistance and friction effects?
- What measurements are most accurate and precise?
- How do you account for experimental uncertainties?
- What factors might cause energy to not be perfectly conserved?
The Spring Launcher Experiment
Compress a spring by a measured distance, then release it to launch a ball vertically. Energy conservation predicts the maximum height based on the spring compression. This experiment beautifully demonstrates elastic → gravitational potential → kinetic energy conversions.
Data Analysis Focus:
- How does maximum height vary with compression distance?
- Is the relationship quadratic as energy conservation predicts?
- What sources of error affect your measurements?
- How can you improve experimental precision?
Graphical Analysis in Energy Problems
Energy problems frequently involve interpreting and creating graphs. Key graph types include:
Force vs. Displacement Graphs: The area under the curve represents work done. For linear relationships (like springs), this creates triangular areas that are easy to calculate.
Energy vs. Position Graphs: These show how kinetic and potential energy change as an object moves through space. The total mechanical energy should remain constant if only conservative forces act.
Power vs. Time Graphs: The area under a power vs. time curve represents total energy transferred or work done.
Real-World Applications: Energy Concepts in Modern Technology
Understanding work, energy, and power opens up insights into countless modern technologies. These applications help reinforce physics concepts while showing their relevance to current innovations.
Renewable Energy Systems
Solar Power: Photovoltaic cells convert light energy directly to electrical energy. The power output depends on light intensity, cell efficiency, and surface area. Energy storage systems (batteries) allow solar power to provide energy even when the sun isn’t shining.
Wind Power: Wind turbines convert kinetic energy of moving air into rotational kinetic energy, then into electrical energy. The power available in wind scales as the cube of wind speed, making high-wind locations dramatically more valuable.
Hydroelectric Power: Falling water converts gravitational potential energy to kinetic energy, then to electrical energy through turbines and generators. The power output depends on both the height of the water drop and the volume flow rate.
Transportation Technology
Electric Vehicles: Battery technology is fundamentally about energy storage density – how much energy can be stored per unit mass or volume. Charging systems must balance power delivery (fast charging) with battery longevity and safety.
Hybrid Systems: These optimize energy efficiency by using electric motors for low-speed operation (where they’re most efficient) and combustion engines for highway speeds. Regenerative braking recovers energy that would otherwise be lost as heat.
Aerospace Applications: Rocket launches demonstrate dramatic energy scaling effects. The energy required to reach orbit is dominated by kinetic energy (orbital velocity ~8 km/s), not potential energy (orbital height ~400 km).
Real-World Physics: The Physics of Athletic Performance
Athletic performance provides compelling examples of energy optimization:
High Jumping: Pole vaulters convert horizontal kinetic energy to gravitational potential energy. The flexible pole temporarily stores energy as elastic potential energy during the vault. Elite vaulters optimize their approach speed, pole flexibility, and technique to maximize this energy conversion.
Cycling: Competitive cyclists obsess over power-to-weight ratios. On flat terrain, power must overcome air resistance (proportional to v³). On climbs, power must overcome gravity (proportional to weight and slope). This explains why climbing specialists are typically lighter, while sprinters emphasize raw power output.
Advanced Topics: Connecting to Other Physics Units
Energy concepts don’t exist in isolation – they connect to virtually every other topic in AP Physics 1. Understanding these connections helps you see physics as a unified field rather than a collection of separate formulas.
Energy and Momentum Connections
While energy and momentum are separate conservation laws, they often appear together in collision problems. Key insights:
- Kinetic energy and momentum both depend on mass and velocity but scale differently (KE ∝ v², p ∝ v)
- Elastic collisions conserve both; inelastic collisions conserve momentum but not kinetic energy
- In explosions, internal chemical potential energy converts to kinetic energy of the fragments
Energy in Simple Harmonic Motion
Simple harmonic motion (covered in Unit 7) provides beautiful examples of energy conservation. In a mass-spring system:
- Total mechanical energy remains constant
- Energy oscillates between kinetic and potential forms
- Maximum kinetic energy occurs when potential energy is minimum, and vice versa
- The period of oscillation depends only on m and k, not on energy
Thermodynamics Connections
While AP Physics 1 doesn’t cover thermodynamics extensively, energy conservation provides the foundation. The first law of thermodynamics is essentially energy conservation applied to systems that can exchange heat. Understanding mechanical energy conservation prepares you for the broader energy concepts in AP Physics 2.
Mastering AP Physics 1 Exam Strategies for Unit 3
Success on the AP Physics 1 exam requires more than just understanding concepts – you need specific strategies for the multiple-choice and free-response sections.
Multiple-Choice Strategy for Energy Problems
Strategy 1: Dimensional Analysis First
Before diving into complex calculations, check units. Energy problems involve joules, watts, and derived units. If answer choices have different units, you can often eliminate options immediately.
Strategy 2: Limiting Cases
Test extreme cases. If a problem involves a spring, what happens when k → 0 or k → ∞? If it involves motion, what happens when v → 0? Correct answers must behave sensibly in limiting cases.
Strategy 3: Energy Conservation Shortcuts
Many multiple-choice problems can be solved using energy conservation without detailed force analysis. Look for situations where initial and final states are clearly defined, especially when the question asks about speeds, heights, or distances.
Free-Response Strategy for Energy Problems
Part (a) – Conceptual Understanding: These typically ask you to explain energy transformations, draw energy bar charts, or describe physical principles. Use proper physics vocabulary and be specific about energy types.
Part (b) – Mathematical Application: These require calculations using energy conservation or work-energy theorem. Show all steps clearly, including:
- Definition of your system
- Identification of initial and final states
- Energy conservation equation
- Algebraic solution before numerical substitution
Part (c) – Experimental Design: These might ask you to design experiments to test energy conservation or measure energy quantities. Consider:
- What variables can you control and measure?
- What equipment would you need?
- How would you minimize experimental errors?
- What graphs would you create to analyze data?
Practice Problems: Building Exam Confidence
Problem 1 (Multiple Choice): A 2-kg block slides down a frictionless inclined plane from rest. If the block’s speed at the bottom is 6 m/s, what is the vertical height of the incline?
A) 0.6 m B) 1.2 m C) 1.8 m D) 3.6 m
Solution: Use conservation of energy. Initial: PE = mgh, KE = 0. Final: PE = 0, KE = ½mv².
mgh = ½mv² → h = v²/2g = 36/(2×10) = 1.8 m. Answer: C
Problem 2 (Conceptual): A ball is thrown upward with initial speed v₀. Compare the work done by gravity during the upward journey to the work done by gravity during the downward journey back to the original height.
Solution: Work done by gravity is W = mgh cos θ. During upward motion, gravity and displacement are opposite (θ = 180°), so work is negative: W₁ = -mgh. During downward motion, gravity and displacement are parallel (θ = 0°), so work is positive: W₂ = +mgh. The magnitudes are equal but signs are opposite, consistent with gravity being a conservative force.
Problem 3 (Free Response – Experimental Design): Design an experiment to determine whether mechanical energy is conserved when a ball rolls down a ramp.
Solution:
- Equipment needed: Ramp, ball, ruler, stopwatch, balance
- Measurements: Ball mass m, ramp height h, ball speed v at bottom
- Procedure: Release ball from rest at top, measure time to travel known distance at bottom to find speed
- Analysis: Compare initial PE (mgh) to final KE (½mv²)
- Expected result: If energy is conserved, mgh = ½mv²
- Sources of error: Air resistance, rolling friction, measurement uncertainties
- Improvements: Use multiple trials, reduce friction, use more precise timing methods
Quick Calculation: Essential Formulas for Unit 3
Keep these relationships readily available:
- Work: W = Fd cos θ
- Kinetic Energy: KE = ½mv²
- Gravitational PE: PE = mgh
- Elastic PE: PE = ½kx²
- Power: P = W/t = Fv cos θ
- Conservation: KE₁ + PE₁ = KE₂ + PE₂ (+ energy dissipated)
Conclusion: Powering Your Physics Success
As we reach the end of our comprehensive journey through AP Physics 1 Unit 3, you’ve developed mastery of some of the most powerful and widely applicable concepts in all of physics. Work, energy, and power aren’t just abstract mathematical relationships – they’re the fundamental principles that govern everything from the smallest molecular motions to the largest cosmic phenomena.
The energy conservation principle you’ve learned represents one of humanity’s greatest intellectual achievements. It provides a unifying framework that connects mechanical motion to thermal processes, electrical phenomena, and even the nuclear reactions that power stars. When you solve a problem using energy conservation, you’re applying the same fundamental principle that engineers use to design spacecraft, that biologists use to understand metabolism, and that environmental scientists use to analyze climate systems.
Key Physics Concepts – Unit 3 Summary:
Work transforms energy from one object to another through force acting over displacement. Master the vector nature of work and recognize when forces do positive, negative, or zero work.
Kinetic Energy represents energy of motion, with its v² dependence creating powerful scaling effects in everything from vehicle safety to athletic performance.
Potential Energy stores energy in position and configuration, allowing systems to convert between kinetic and potential forms while conserving total mechanical energy.
Conservation of Energy provides the most powerful problem-solving tool in physics, often simplifying complex force problems into elegant energy balance equations.
Power quantifies the rate of energy transfer, connecting physics to practical engineering considerations in motors, generators, and biological systems.
Your success in Unit 3 has prepared you well for the remaining units in AP Physics 1. The energy concepts you’ve mastered will reappear in simple harmonic motion, where energy oscillates between kinetic and potential forms. They’ll be crucial for understanding wave phenomena, where energy propagates through space without matter transfer. And they’ll provide the foundation for electromagnetic concepts, where energy storage in electric and magnetic fields becomes essential.
Final Exam Strategy Reminders:
Remember that energy problems often provide shortcuts to solutions that would be extremely difficult using force analysis alone. When you see a problem asking about final speeds, maximum heights, or stopping distances, immediately consider whether energy methods might provide a more direct path to the answer.
Practice recognizing the signs that energy conservation applies: problems involving motion along curved paths, situations where forces are difficult to analyze directly, or questions that ask about initial and final states without requiring details about the intermediate process.
Most importantly, develop confidence in your energy intuition. You now understand why heavy objects don’t fall faster than light ones (same potential energy per unit mass converts to same kinetic energy per unit mass), why it’s harder to stop a fast car than a slow one (kinetic energy scales as v²), and why perpetual motion machines are impossible (energy conservation forbids creating energy from nothing).
Next Steps for Continued Physics Learning:
As you prepare for the AP Physics 1 exam, continue practicing with authentic College Board materials. Focus on the free-response questions, which often integrate energy concepts with experimental design and graphical analysis. Develop fluency with energy bar charts and graphical representations of energy transformations.
Consider how the problem-solving strategies you’ve developed in Unit 3 apply to other areas of physics and engineering. Energy optimization appears in contexts from architectural design (minimizing heating energy) to computer science (minimizing computational energy), making your physics knowledge broadly applicable.
Remember that physics understanding develops gradually through practice and reflection. Each problem you solve, each concept you explain to a classmate, and each connection you make to real-world applications strengthens your overall physics intuition. The energy concepts from Unit 3 will serve as valuable tools throughout your scientific education and career.
With your solid foundation in work, energy, and power, you’re well-prepared to tackle the AP Physics 1 exam and to continue exploring the fascinating world of physics. The energy concepts you’ve mastered will continue to provide insights and problem-solving power throughout your scientific journey, whether you’re analyzing the efficiency of hybrid vehicles, understanding the physics of sports performance, or exploring the energy transformations that power our technological civilization.
Energy is conserved, knowledge is powerful, and your physics success is now within reach!
Ready to test your Unit 3 mastery? Practice with authentic AP Physics 1 exam questions and remember: when in doubt, think energy first – it’s often the most elegant path to the solution.
Recommended –


1 thought on “Mastering AP Physics 1 Unit 3: Work, Energy, and Power – The Complete Guide to Energy Concepts That Power Our World”